Arc Length Calculator

With this calculator, you can:

  • Compute arc length from the radius and angle (in degrees or radians).
  • Determine arc length using sector area or chord length.
  • Convert results into various units like meters, centimeters, feet, and miles.

Arc Length Equation

\[L = r\theta \quad \text{(where } \theta \text{ is in radians, and } L \text{ is in the same units as } r)\]

\[L = \frac{\pi r \theta}{180°} \quad \text{(where } \theta \text{ is in degrees, and } L \text{ is in the same units as } r)\]

Where:

  • \(L\) = Arc length
  • \(r\) = Radius of the circle
  • \(\theta\) = Central angle (in radians or degrees)

Note: To convert degrees to radians, use the formula \(\text{radians} = \frac{\pi}{180} \cdot \text{degrees}\).

Using Angle and Radius
Using Chord Length
Using Sector Area

Results:

Frequently Asked Questions

What is the arc length?

The arc length is the distance measured along the curved line of a circle segment. It is a portion of the circumference of a circle defined by a central angle or other parameters such as chord length or sector area.

Example: Imagine a slice of pizza — the curved edge is the arc length.

How do you calculate the arc length using the radius and central angle?

The arc length can be calculated using the formula:

  • If the angle is in radians: \[ L = r \cdot \theta \]
  • If the angle is in degrees: \[ L = \frac{\pi \cdot r \cdot \theta}{180} \]

Here, \(L\) is the arc length, \(r\) is the radius of the circle, and \(\theta\) is the central angle.

How do you calculate the arc length from the sector area?

To calculate the arc length (\(L\)) from the sector area (\(A\)) and radius (\(r\)), follow these steps:

  1. First, calculate the central angle (\(\theta\)) in radians using the formula: \[ \theta = \frac{2A}{r^2} \] Here, \(A\) is the sector area, and \(r\) is the radius of the circle.
  2. Then, calculate the arc length using: \[ L = r \cdot \theta \]

Example:

  • Let the sector area be \(A = 50 \, \text{m}^2\), and the radius \(r = 10 \, \text{m}\).
  • Step 1: Calculate the central angle: \[ \theta = \frac{2A}{r^2} = \frac{2 \cdot 50}{10^2} = \frac{100}{100} = 1 \, \text{radian.} \]
  • Step 2: Calculate the arc length: \[ L = r \cdot \theta = 10 \cdot 1 = 10 \, \text{m.} \]

Thus, the arc length is \(10 \, \text{m}\).

What units are used for arc length?

The arc length is typically measured in the same units as the radius of the circle. Common units include:

  • Millimeters (mm)
  • Centimeters (cm)
  • Meters (m)
  • Kilometers (km)
  • Inches (in)
  • Feet (ft)
  • Yards (yd)

You can use the calculator to convert between these units for convenience.

What is the relationship between sector area and arc length?

The sector area (\(A\)) is related to the arc length (\(L\)) and the radius (\(r\)) of the circle. The formula is:

\[ A = \frac{1}{2} \cdot r \cdot L \]

From this formula, you can see that for a given sector area, increasing the radius decreases the arc length, and vice versa.

What is the role of radians in arc length calculation?

Radians are a natural unit for measuring angles in mathematics because they directly relate the angle to the radius and arc length. When the angle is in radians, the arc length is simply the product of the radius and the angle: \[ L = r \cdot \theta \] This simplifies calculations and avoids the need for additional conversions.

Can I calculate arc length if the circle is not a perfect circle?

The formulas for arc length assume a perfect circle. If the curve is part of an ellipse or another irregular shape, you will need a different mathematical approach, such as integral calculus, to calculate the arc length.

What is the difference between arc length and circumference?

The arc length is a portion of the circumference of a circle, defined by a specific angle or other parameters. The circumference is the total length of the circle's boundary, calculated as: \[ C = 2\pi r \]

Example: If the central angle is \(90^\circ\), the arc length would be one-fourth of the circle's circumference.

Calculating Arc Length Programmatically in Python

Python provides several tools and libraries to calculate arc length using different input parameters such as radius, angle, chord length, and sector area. Here are multiple methods to perform these calculations:

Method 1: Basic Calculation Using Radius and Angle

This method uses the basic formula \(L = r \cdot \theta\), where the angle is assumed to be in radians. This is a direct and efficient way to calculate the arc length if the angle is already given in radians.

Using Radius and Angle (Radians)
# Function to calculate arc length using radius and angle (in radians)
def arc_length_radius_angle(radius, angle_radians):
    return radius * angle_radians

# Example usage
radius = 10
angle_radians = 1.5  # Example angle in radians
arc_length = arc_length_radius_angle(radius, angle_radians)
print(f"The arc length is: {arc_length} units")
The arc length is: 15.0 units

Method 2: Conversion and Calculation with Angle in Degrees

If the angle is given in degrees, you need to convert it to radians first. The math.radians() function in Python simplifies this conversion. After conversion, the formula \(L = r \cdot \theta\) is used.

Using Radius and Angle (Degrees)
import math

# Function to calculate arc length using radius and angle (in degrees)
def arc_length_degrees(radius, angle_degrees):
    angle_radians = math.radians(angle_degrees)  # Convert degrees to radians
    return radius * angle_radians

# Example usage
radius = 10
angle_degrees = 90  # Example angle in degrees
arc_length = arc_length_degrees(radius, angle_degrees)
print(f"The arc length is: {arc_length} units")
The arc length is: 15.707963267948966 units

Method 3: Using Sector Area

To calculate arc length from the sector area, we first calculate the central angle using the formula:

  • \(\theta = \frac{2 \cdot A}{r^2}\), where \(A\) is the sector area and \(r\) is the radius.

After determining the angle in radians, we apply the formula \(L = r \cdot \theta\) to find the arc length.

Using Sector Area
# Function to calculate arc length from sector area and radius
def arc_length_sector_area(sector_area, radius):
    # Calculate central angle in radians
    central_angle = (2 * sector_area) / (radius ** 2)
    # Calculate arc length
    return radius * central_angle

# Example usage
sector_area = 50  # Sector area in square units
radius = 10       # Radius in units
arc_length = arc_length_sector_area(sector_area, radius)
print(f"The arc length is: {arc_length} units")
The arc length is: 10.0 units

Method 4: Using NumPy for Efficient Computations

NumPy is a powerful library for numerical calculations. It allows for efficient and vectorized operations, making it ideal for calculations involving large datasets or when angles are provided in degrees or radians.

Using NumPy for Arc Length Calculations
import numpy as np

# Function to calculate arc length using NumPy
def arc_length_numpy(radius, angle_degrees=None, angle_radians=None):
    if angle_degrees is not None:
        angle_radians = np.radians(angle_degrees)  # Convert degrees to radians
    return radius * angle_radians

# Example usage
radius = 10
angle_degrees = 120
arc_length = arc_length_numpy(radius, angle_degrees=angle_degrees)
print(f"The arc length is: {arc_length} units")
The arc length is: 20.94395102393195 units

Method 5: Visualizing Arc Length with Matplotlib

To better understand the concept of arc length, visualization can be helpful. Using Matplotlib, you can create a graphical representation of the circle and its corresponding arc for a given central angle.

Visualizing Arc Length
import matplotlib.pyplot as plt
import numpy as np

# Function to plot circle and arc
def plot_arc(radius, angle_degrees):
    angle_radians = np.radians(angle_degrees)
    theta = np.linspace(0, angle_radians, 100)
    x = radius * np.cos(theta)
    y = radius * np.sin(theta)

    # Plot circle and arc
    circle = plt.Circle((0, 0), radius, color='lightgray', fill=False)
    fig, ax = plt.subplots()
    ax.add_artist(circle)
    ax.plot(x, y, color='black', label='Arc')
    ax.scatter([0, radius * np.cos(angle_radians)], [0, radius * np.sin(angle_radians)], color='red', zorder=5)
    ax.legend()
    ax.set_aspect('equal', adjustable='datalim')
    plt.title(f"Arc Length Visualization (Angle = {angle_degrees}°)")
    plt.show()

# Example usage
plot_arc(10, 120)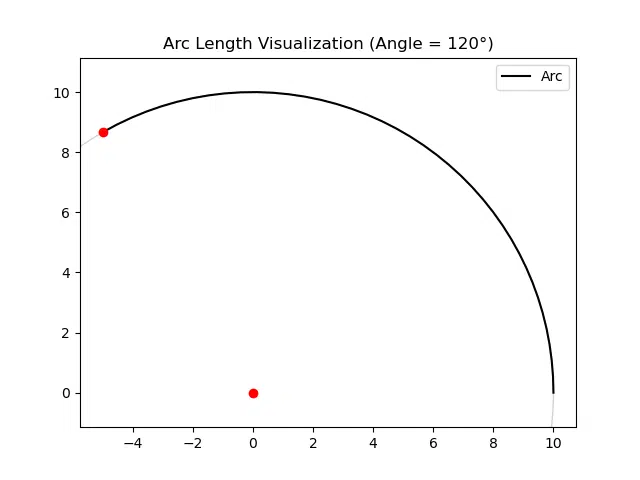
A visual representation of a circle with an arc highlighted. The arc is part of the circle's circumference, corresponding to a given central angle in degrees. The circle is outlined in light gray, the arc in black, and the start and end points of the arc are marked in red.
Visualization of an arc on a circle: The arc (black) corresponds to a central angle of 120°. The start and end points of the arc are marked in red, and the circle is outlined in light gray.

Further Reading and Libraries

Here are some additional Python libraries and resources for geometric calculations:

Attribution

If you found this guide and tools helpful, feel free to link back to this page for attribution and share it with others!

Feel free to use these formats to reference our tools in your articles, blogs, or websites.

Profile Picture
Senior Advisor, Data Science | [email protected] | + posts

Suf is a senior advisor in data science with deep expertise in Natural Language Processing, Complex Networks, and Anomaly Detection. Formerly a postdoctoral research fellow, he applied advanced physics techniques to tackle real-world, data-heavy industry challenges. Before that, he was a particle physicist at the ATLAS Experiment of the Large Hadron Collider. Now, he’s focused on bringing more fun and curiosity to the world of science and research online.

© 2024 The Research Scientist Pod. All rights reserved.