Introduction
Autoencoders are neural networks designed to compress data into a lower-dimensional latent space and reconstruct it. They are useful for tasks like dimensionality reduction, anomaly detection, and generative modeling. In this tutorial, we implement a basic autoencoder in PyTorch using the MNIST dataset. We’ll cover preprocessing, architecture design, training, and visualization, providing a solid foundation for understanding and applying autoencoders in practice.
Table of Contents
- Learn to implement a basic autoencoder using PyTorch
- Understand the architecture and training process
- Work with the MNIST dataset for image reconstruction
- Visualize and analyze results
Theoretical Background
Autoencoders are neural networks that learn to compress data into a latent space and reconstruct it. Mathematically, given an input \( x \), the encoder function \( f(x) \) maps it to a latent representation \( z \) in a lower-dimensional space:
Encoder: \( z = f(x) = \sigma(W_{\text{enc}}x + b_{\text{enc}}) \)
Decoder: \( \hat{x} = g(z) = \sigma(W_{\text{dec}}z + b_{\text{dec}}) \)
Here, \( W_{\text{enc}} \) and \( b_{\text{enc}} \) are the encoder’s weights and biases, and \( W_{\text{dec}} \) and \( b_{\text{dec}} \) are the decoder’s weights and biases. The objective is to minimize the reconstruction loss between the input \( x \) and the reconstructed output \( \hat{x} \), often using Mean Squared Error (MSE):
Autoencoders remain highly relevant in modern deep learning. They are foundational for applications like anomaly detection, image denoising, and pretraining for more complex models. Variational Autoencoders (VAEs) and Denoising Autoencoders take autoencoders further, making them useful for generating data and extracting features, which helps with tasks like data compression and creating synthetic data.
Analogy for Autoencoders: Think of an autoencoder as a smart compression algorithm. Imagine shrinking a high-resolution image into a tiny thumbnail that retains the most important details, then reconstructing the full image from that thumbnail. The encoder is like the compression step, where the data is reduced to a smaller, meaningful representation (the latent space), and the decoder is the decompression step, attempting to restore the original. The better the autoencoder, the closer the reconstruction is to the original image while still keeping the latent space compact and efficient.
Setting Up the Environment
Before starting, make sure PyTorch is installed on your system. Choose the appropriate command based on your hardware:
-
For GPU Support:
pip install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu118 -
For CPU Support Only:
pip install torch torchvision torchaudio
For detailed installation instructions, visit the PyTorch Installation Guide.
Before diving into the implementation, we need to set up our PyTorch environment with all necessary imports. We’ll use PyTorch’s neural network modules, optimization tools, and the torchvision package for handling the MNIST dataset.
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
# Set random seed for reproducibility
torch.manual_seed(42)
# Device configuration
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')- Setting a random seed ensures reproducibility across different runs
- The code automatically detects and uses GPU if available, falling back to CPU if not
- We import both high-level (nn, optim) and utility modules (transforms, DataLoader) for complete functionality
Loading and Preprocessing MNIST
The MNIST dataset consists of 28×28 pixel grayscale images of handwritten digits. Before training, we need to properly prepare and load this data. We’ll apply necessary transformations and set up a data loader for efficient batch processing.
# Define transforms
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
# Load MNIST dataset
train_dataset = torchvision.datasets.MNIST(
root='./data',
train=True,
transform=transform,
download=True
)
train_loader = DataLoader(
dataset=train_dataset,
batch_size=128,
shuffle=True
)- ToTensor() converts images to PyTorch tensors and scales pixels from [0, 255] to [0, 1]
- Normalize() transforms the data to have mean 0 and standard deviation 1
- Batch size of 128 provides a good balance between memory usage and training speed
- Shuffling the data helps prevent the model from learning order-dependent patterns
Defining the Autoencoder Architecture
Our autoencoder architecture consists of symmetric encoder and decoder networks. The encoder compresses the 784-dimensional input (28×28 pixels) into a 20-dimensional latent space, while the decoder learns to reconstruct the original image from this compressed representation.
class Autoencoder(nn.Module):
def __init__(self, latent_dim=20):
super(Autoencoder, self).__init__()
# Encoder
self.encoder = nn.Sequential(
nn.Linear(28*28, 400),
nn.ReLU(),
nn.Linear(400, 200),
nn.ReLU(),
nn.Linear(200, latent_dim)
)
# Decoder
self.decoder = nn.Sequential(
nn.Linear(latent_dim, 200),
nn.ReLU(),
nn.Linear(200, 400),
nn.ReLU(),
nn.Linear(400, 28*28),
nn.Tanh()
)
def forward(self, x):
# Flatten input
x = x.view(x.size(0), -1)
# Get latent representation
latent = self.encoder(x)
# Reconstruct input
reconstructed = self.decoder(latent)
# Reshape to original dimensions
reconstructed = reconstructed.view(x.size(0), 1, 28, 28)
return reconstructed- Progressive Dimension Reduction: The encoder reduces input dimensions step-by-step (784 ⇛ 400 ⇛ 200 ⇛ 20), gradually compressing the data into a compact 20-dimensional latent space while preserving important features.
- Symmetric Expansion: The decoder mirrors the encoder’s structure (20 ⇛ 200 ⇛ 400 ⇛ 784) to reconstruct the original input from the latent space, ensuring an effective mapping back to the input dimensions.
- ReLU activations are used in intermediate layers to introduce non-linearity and avoid vanishing gradients, enabling the network to learn complex patterns more effectively.
- Tanh Output Activation: Ensures that reconstructed values are constrained to the range [-1, 1], matching the normalized input data and improving reconstruction quality.
Training Loop
Training an autoencoder involves minimizing the reconstruction loss between the input and output images. We use the Mean Squared Error (MSE) loss and the Adam optimizer, which adapts the learning rate for each parameter.
# Initialize model and move to device
model = Autoencoder().to(device)
# Loss function and optimizer
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
# Training loop
num_epochs = 20
for epoch in range(num_epochs):
total_loss = 0
for batch_idx, (images, _) in enumerate(train_loader):
# Move images to device
images = images.to(device)
# Forward pass
outputs = model(images)
loss = criterion(outputs, images)
# Backward pass and optimize
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
# Print epoch statistics
avg_loss = total_loss / len(train_loader)
print(f'Epoch [{epoch+1}/{num_epochs}], Average Loss: {avg_loss:.4f}')Epoch [2/20], Average Loss: 0.0663
Epoch [3/20], Average Loss: 0.0528
Epoch [4/20], Average Loss: 0.0456
Epoch [5/20], Average Loss: 0.0416
Epoch [6/20], Average Loss: 0.0391
Epoch [7/20], Average Loss: 0.0372
Epoch [8/20], Average Loss: 0.0358
Epoch [9/20], Average Loss: 0.0347
Epoch [10/20], Average Loss: 0.0337
Epoch [11/20], Average Loss: 0.0330
Epoch [12/20], Average Loss: 0.0323
Epoch [13/20], Average Loss: 0.0317
Epoch [14/20], Average Loss: 0.0311
Epoch [15/20], Average Loss: 0.0307
Epoch [16/20], Average Loss: 0.0303
Epoch [17/20], Average Loss: 0.0299
Epoch [18/20], Average Loss: 0.0295
Epoch [19/20], Average Loss: 0.0292
Epoch [20/20], Average Loss: 0.0289
- MSE Loss: Mean Squared Error (MSE) is used as the loss function to measure pixel-wise reconstruction quality. It calculates the average squared difference between the input and reconstructed images, ensuring the model focuses on minimizing reconstruction errors.
-
Learning Rate: A learning rate of
1e-3is chosen as a reliable starting point for the Adam optimizer. This value balances convergence speed and stability, allowing the model to learn effectively without overshooting the minima. - Number of Epochs: Training for 20 epochs is generally sufficient for MNIST, as the dataset is relatively simple. This provides enough iterations for the model to learn the latent representation while avoiding overfitting.
- Loss Tracking: We calculate the average loss per epoch to monitor training progress. This helps identify trends such as convergence (loss decreasing steadily) or potential issues like overfitting (validation loss diverging from training loss).
Visualizing Results
Visualization is crucial for understanding how well our autoencoder performs. We’ll create a function to display original images alongside their reconstructions, allowing us to visually assess the quality of the learned representations.
import matplotlib.pyplot as plt
def visualize_reconstruction(model, data_loader):
model.eval()
with torch.no_grad():
images, _ = next(iter(data_loader))
images = images.to(device)
reconstructed = model(images)
# Plot original vs reconstructed images
fig, axes = plt.subplots(2, 8, figsize=(15, 4))
for i in range(8):
# Original images
axes[0,i].imshow(images[i].cpu().numpy().squeeze(), cmap='gray')
axes[0,i].axis('off')
# Reconstructed images
axes[1,i].imshow(reconstructed[i].cpu().numpy().squeeze(), cmap='gray')
axes[1,i].axis('off')
plt.tight_layout()
plt.show()
# Visualize results
visualize_reconstruction(model, train_loader)
- Use model.eval() to disable dropout and batch normalization during visualization
- Disable gradient computation to save memory
- Compare original and reconstructed images side by side
- Use consistent image scaling and colormaps for fair comparison
Analysis of Results
A well-trained autoencoder demonstrates several key characteristics that indicate successful learning of the data’s underlying structure. Let’s examine what to look for in the results:
- The reconstructed images should maintain the essential features of the digits while possibly showing some blur or loss of fine details
- The 20-dimensional latent space should capture meaningful variations in the digit shapes
- Similar digits should have similar latent representations, indicating good feature learning
- Blurry reconstructions might indicate insufficient network capacity
- Poor reconstruction of certain digits might suggest imbalanced training data
- Over-sharp or noisy reconstructions could indicate overfitting
Visualizing the Latent Space with t-SNE
To better understand how the autoencoder is learning and compressing the input data, we can visualize the 20-dimensional latent space using t-SNE (t-Distributed Stochastic Neighbor Embedding), a dimensionality reduction technique that projects high-dimensional data into two dimensions for visualization.
import numpy as np
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
def visualize_latent_space(model, data_loader, n_samples=1000):
model.eval()
with torch.no_grad():
# Get a batch of data
images, labels = next(iter(data_loader))
images, labels = images[:n_samples], labels[:n_samples] # Limit the number of samples
images = images.to(device)
# Pass images through encoder to get latent vectors
latent_vectors = model.encoder(images.view(images.size(0), -1)).cpu().numpy()
labels = labels.numpy()
# Apply t-SNE to reduce latent space to 2D, default perplexity = 30
tsne = TSNE(n_components=2, random_state=42)
latent_2d = tsne.fit_transform(latent_vectors)
# Plot the 2D latent space with labels
plt.figure(figsize=(10, 8))
scatter = plt.scatter(latent_2d[:, 0], latent_2d[:, 1], c=labels, cmap='tab10', alpha=0.7)
plt.colorbar(scatter, ticks=range(10), label='Digit Labels')
plt.title('2D Visualization of Latent Space using t-SNE')
plt.xlabel('t-SNE Dimension 1')
plt.ylabel('t-SNE Dimension 2')
plt.show()
# Visualize the latent space
visualize_latent_space(model, train_loader)
The plot below shows a 2D visualization of the latent space produced by the autoencoder. Each point represents a digit from the MNIST dataset, projected into two dimensions using t-SNE. Colors indicate digit labels, with similar digits ideally forming distinct clusters. This visualization helps evaluate the autoencoder’s ability to capture meaningful features in the latent space.
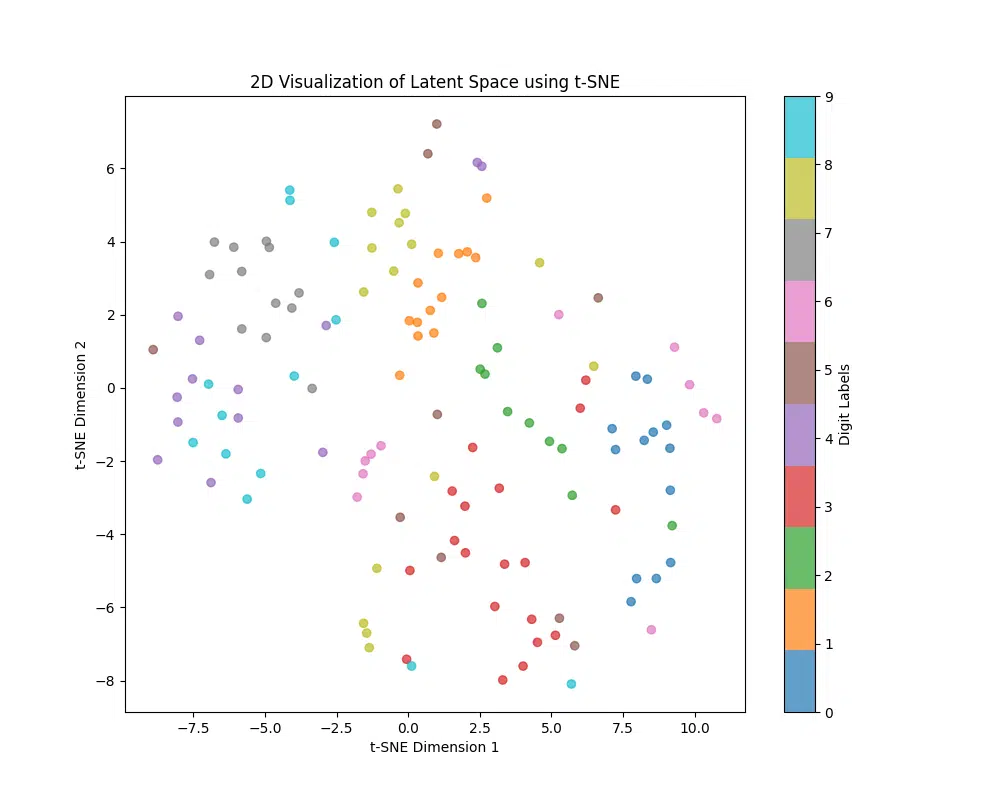
- Balanced Dataset: Ensure the dataset has a balanced sample of digits to avoid biases in the clustering. This ensures all digits are equally represented in the latent space.
-
Adjust Perplexity: Experiment with different values of
perplexityin t-SNE (commonly between 5 and 50) to find the optimal balance for clustering visualization. Perplexity affects how clusters are formed and visualized. - Consider UMAP: If t-SNE results are unsatisfactory or too slow for larger datasets, try using UMAP (Uniform Manifold Approximation and Projection). UMAP often provides faster and more interpretable results while preserving global and local structures.
Setting the perplexity to 6, – tsne = TSNE(n_components=2, random_state=42, perplexity=6) we get the following latent space visualization:
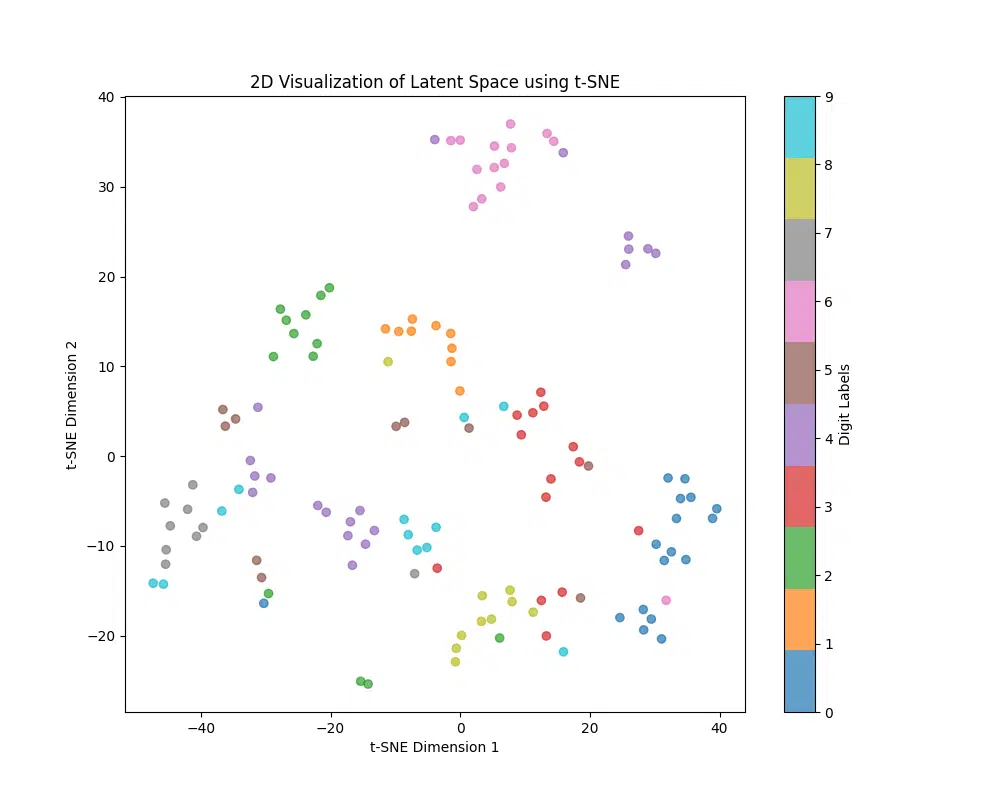
perplexity parameter in t-SNE influences how the algorithm balances local and global relationships in the data. A lower perplexity, such as 6, focuses more on local clusters, resulting in tightly grouped points for similar data. This can enhance visualization for datasets like MNIST, where distinct groups are expected. However, if perplexity is set too low, it might ignore broader structures, so experimentation is key.
Insights from t-SNE Visualization
The t-SNE visualization of the latent space reveals the following key insights:
- Distinct Clusters: Well-defined clusters for similar digits (e.g., ‘1’s or ‘0’s) indicate the autoencoder successfully encodes similar data into nearby regions.
- Overlapping Clusters: Overlaps between certain digits (e.g., ‘3’ and ‘8’) suggest shared visual features or model limitations in separating complex patterns.
- Spread of Points: Tight clusters reflect compact and meaningful representations, while scattered points may indicate inconsistencies in data compression.
- Outliers: Isolated points might represent poorly written digits or highlight areas where the model struggles to generalize.
- Feature Learning: Well-formed clusters demonstrate that the latent space captures meaningful features, useful for tasks like classification or generation.
- Model Limitations: Overlaps or scattered points suggest opportunities to improve the model by increasing capacity, adding regularization, or training with more data.
Next Steps: Tight, non-overlapping clusters indicate strong performance, while overlaps or scattered points can be addressed by adjusting hyperparameters, experimenting with latent space dimensions, or exploring advanced architectures like Variational Autoencoders (VAEs).
Advanced Concepts and Future Improvements
While our implementation provides a solid foundation, incorporating advanced techniques can significantly improve the autoencoder’s efficiency, robustness, and real-world applicability. These concepts not only enhance the performance but also help in extracting more meaningful representations from the data.
- Convolutional Architecture: Replace linear layers with convolutional layers to better capture spatial relationships in images. This is particularly effective for datasets like MNIST, where pixel locality is crucial. Transposed convolutional layers can be used in the decoder to reconstruct images more effectively.
- Variational Autoencoder: Introduce a probabilistic component by adding a KL divergence loss. This ensures the latent space is continuous and enables meaningful interpolation between data points. VAEs are especially useful for generative tasks.
- Regularization Techniques: Incorporate dropout layers to randomly deactivate neurons during training, or use L2 regularization (weight decay) to penalize overly complex models. These techniques help prevent overfitting and improve generalization.
- Latent Space Analysis: Use t-SNE or UMAP to visualize the latent space and evaluate how well the model clusters similar data. This analysis provides insights into the quality of feature extraction and representation learning.
- Advanced Loss Functions: Experiment with perceptual losses or structural similarity metrics (SSIM) to improve reconstruction quality by focusing on structural rather than pixel-wise differences.
Implementing these improvements can make the autoencoder more versatile and suitable for a variety of applications, such as anomaly detection, generative modeling, and transfer learning.
- Validation Splits and Early Stopping: Divide your dataset into training and validation sets to monitor generalization performance. Use early stopping to terminate training when validation loss stops improving.
- Model Checkpointing: Save the model’s best weights during training to ensure you can recover the best-performing version in case of interruptions or overfitting.
- Monitor Metrics: Track both training and validation losses during training. Adding metrics like Mean Absolute Error (MAE) or F1-score (if applicable) provides a more comprehensive evaluation of performance.
- Learning Rate Scheduling: Use a learning rate scheduler to dynamically adjust the learning rate during training, helping the model converge more efficiently and avoid overshooting minima.
Conclusion
Autoencoders are an exciting way to learn meaningful patterns and compress data into a compact form. In this guide, we walked through building a simple autoencoder in PyTorch, explored its latent space with t-SNE, and looked at ways to make it even better. With a few tweaks – like adding convolutional layers or regularization – you can take your autoencoder to the next level. Whether you’re working on anomaly detection, data compression, or generating new data, autoencoders offer a versatile tool for many deep learning tasks. Keep experimenting and exploring there is always more to learn!
Further Reading
Here are some helpful resources to deepen your understanding of autoencoders and their applications:
-
Variational Autoencoders (VAE) Paper
The original paper introducing VAEs, explaining their theory and applications in detail.
-
t-SNE Documentation
Official documentation on t-SNE for dimensionality reduction and visualizing high-dimensional data.
-
The Research Scientist Pod: Deep Learning Frameworks
Explore other deep learning frameworks and their unique advantages for building models.
If you found this guide helpful, feel free to link back to this post for attribution and share it with others exploring autoencoders in PyTorch!
HTML: Attribution: The Research Scientist Pod – Building Autoencoders in PyTorch: A Beginner-Friendly Tutorial
Markdown: [The Research Scientist Pod – Building Autoencoders in PyTorch: A Beginner-Friendly Tutorial](https://researchdatapod.com/building-autoencoders-pytorch-tutorial/)
Have fun and happy researching!
Suf is a senior advisor in data science with deep expertise in Natural Language Processing, Complex Networks, and Anomaly Detection. Formerly a postdoctoral research fellow, he applied advanced physics techniques to tackle real-world, data-heavy industry challenges. Before that, he was a particle physicist at the ATLAS Experiment of the Large Hadron Collider. Now, he’s focused on bringing more fun and curiosity to the world of science and research online.

