In this guide, we’ll dive into the process of calculating the p-value from a Z-score in Python, using clear and practical examples to make the concepts accessible. Whether you’re a student, a researcher, or just someone curious about statistics, understanding how p-values work can help you make sense of hypothesis testing and the significance of your results. By the end of this tutorial, you’ll not only know how to compute p-values in Python but also gain insights into how they reflect the probability of observing a value as extreme as the Z-score under the null hypothesis.
Table of Contents
Introduction to Z-Scores and P-Values
The Z-score is calculated as:
\[ Z = \frac{X – \mu}{\sigma} \]
where:
- $X$ is the observed value or data point in question,
- $ \mu $ is the mean (average) of the population, and
- $ \sigma $ is the standard deviation of the population, which measures the spread or dispersion of the data around the mean.
The Z-score indicates how many standard deviations a given data point is from the population mean. A Z-score of 0 means the data point is exactly at the mean. Positive Z-scores represent values above the mean, while negative Z-scores indicate values below the
Understanding the Z-Score
The Z-score, also known as the standard score, measures how many standard deviations a data point is from the population mean. A Z-score of 0 means the value is exactly at the mean, while positive Z-scores indicate values above the mean, and negative Z-scores indicate values below the mean.
Think of the Z-score as a way to standardize different datasets so they can be compared on a common scale. For example, if two students score differently on two tests with different averages and standard deviations, their Z-scores can help you understand how well each student performed relative to their respective groups.
The p-value, which is calculated from the Z-score, tells us the probability of observing a value as extreme as the one calculated, assuming the null hypothesis is true. Essentially, it answers the question: “How surprising is this observation in the context of the dataset?” Lower p-values suggest that the observation is rare under the null hypothesis, which might lead us to reconsider it.
Calculating the P-Value from a Z-Score
Formula for Calculating the P-Value
To find the p-value from a Z-score, we use the standard normal distribution, which has a mean of 0 and a standard deviation of 1. The p-value depends on whether the test is one-tailed or two-tailed:
- One-Tailed Test: The p-value is the area under the curve in one direction beyond the observed Z-score. It is calculated as: \[ p = 1 – \Phi(|z|) \] where \( \Phi(|z|) \) is the cumulative distribution function (CDF) of the standard normal distribution.
- Two-Tailed Test: The p-value considers extreme values in both directions of the distribution and is calculated as: \[ p = 2 \times (1 – \Phi(|z|)) \] This formula accounts for the combined areas in both tails beyond the observed Z-score.
In Python, the scipy.stats library provides tools for calculating p-values. Here’s how we compute p-values for one-tailed and two-tailed tests:
norm.cdf(z_score): Calculates the area to the left of the Z-score under the standard normal curve (lower tail probability).norm.sf(z_score): Calculates the area to the right of the Z-score under the standard normal curve (upper tail probability), equivalent to \( 1 – \text{CDF}(z) \).
Here’s how norm.sf (survival function) works:
- For a one-tailed test, it calculates the upper tail probability (area beyond the Z-score).
- For a two-tailed test, we multiply the one-tailed probability by 2 to account for both ends of the distribution.
In a two-tailed test, we use the absolute value of the Z-score because we are interested in extreme values on both sides of the mean. Specifically:
- Negative Z-scores: Represent values below the mean. By taking the absolute value, we map these negative scores to their positive counterparts, allowing us to calculate the corresponding upper tail probability.
- Symmetry of the normal distribution: The standard normal distribution is symmetric about the mean (Z = 0). The probability of observing a Z-score below a certain value is the same as observing its positive counterpart above the mean. Thus, the upper tail probability for a negative Z-score can be computed using the positive Z-score.
By using abs(z_score), we ensure that the calculation accurately considers the probabilities in both tails of the distribution, giving us the correct p-value for a two-tailed test.
from scipy.stats import norm
# Z-score
z_score = 2.5
# One-tailed p-value
p_value_one_tailed = norm.sf(z_score)
# Two-tailed p-value
p_value_two_tailed = 2 * norm.sf(abs(z_score))
print(f"One-Tailed P-Value: {p_value_one_tailed}")
print(f"Two-Tailed P-Value: {p_value_two_tailed}")Two-Tailed P-Value: 0.012419330651552265
Interpreting One-Tailed and Two-Tailed P-Values
One-Tailed P-Value
- Value: 0.006209665325776132
- Interpretation: The probability of observing a value as extreme as the given Z-score (2.5) in one direction (either above or below the mean) is approximately 0.62%.
- Significance: If the significance level (\( \alpha \)) is 0.05 (5%), this p-value is below the threshold, indicating that the result is statistically significant for a one-tailed test. This suggests sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis.
Two-Tailed P-Value
- Value: 0.012419330651552265
- Interpretation: The probability of observing a value as extreme as the given Z-score (2.5) in either direction (both above and below the mean) is approximately 1.24%.
- Significance: For a significance level (\( \alpha \)) of 0.05, this p-value is also below the threshold. This means the result is statistically significant for a two-tailed test, indicating evidence against the null hypothesis.
Key Takeaway
The one-tailed p-value is half the two-tailed p-value because the one-tailed test considers only one end of the distribution, while the two-tailed test accounts for both ends. These values help determine whether the observed result provides enough evidence to reject the null hypothesis under the specified test and significance level.
Using norm.cdf vs norm.sf
In Python’s scipy.stats module, both norm.cdf and norm.sf can be used to calculate probabilities for the standard normal distribution. However, they serve slightly different purposes:
Using norm.cdf
The norm.cdf(z_score) function calculates the cumulative distribution function (CDF), which gives the probability that a value is less than or equal to the Z-score:
from scipy.stats import norm
# Z-score
z_score = 2.5
# One-tailed p-value using CDF
p_value_one_tailed = 1 - norm.cdf(z_score)
# Two-tailed p-value
p_value_two_tailed = 2 * (1 - norm.cdf(abs(z_score)))
print(f"One-Tailed P-Value (using CDF): {p_value_one_tailed}")
print(f"Two-Tailed P-Value (using CDF): {p_value_two_tailed}")
Two-Tailed P-Value (using CDF): 0.012419330651552318
Here, 1 - norm.cdf(z_score) is used to calculate the upper tail probability, which represents the p-value for a one-tailed test. For a two-tailed test, we multiply this value by 2 to account for both ends of the distribution.
Why Prefer norm.sf?
- Direct Calculation: The survival function gives the upper tail probability directly, eliminating the need to calculate \( 1 – \text{CDF}(z) \), which simplifies the code.
- Readability: Using
sfmakes the code more intuitive, as it directly reflects the concept of the upper tail probability used in hypothesis testing.
While both approaches yield the same results, norm.sf is often preferred for its simplicity and clarity when calculating one-tailed or two-tailed p-values for Z-scores.
When Is the Lower Tail Required?
The lower tail, which refers to the area under the curve to the left of the Z-score (\( P(Z \leq z) \)), is relevant in several scenarios when working with Z-scores, cumulative distribution functions (CDFs), and hypothesis testing. Below are key examples where the lower tail is required:
1. Left-Tailed Hypothesis Tests
In a left-tailed test, the hypothesis focuses on values smaller than the mean. For instance:
- Null Hypothesis (\( H_0 \)): The mean of the population is greater than or equal to a certain value.
- Alternative Hypothesis (\( H_a \)): The mean of the population is less than a certain value.
In such cases, the lower tail probability (\( P(Z \leq z) \)) is the p-value, representing the likelihood of observing a value less than or equal to the Z-score under the null hypothesis.
from scipy.stats import norm
# Z-score
z_score = -1.5
# Lower tail p-value
p_value_lower_tail = norm.cdf(z_score)
print(f"Lower Tail P-Value: {p_value_lower_tail}")
2. Left-Skewed Distributions
In naturally left-skewed distributions (e.g., failure rates or some biological measurements), the lower tail captures rare or extreme events occurring below the mean. This is essential when analyzing risks or deviations in the lower range of data.
3. Percentiles and Quantiles
The lower tail is used to calculate percentiles or quantiles, which are measures of position in a dataset:
- The 25th percentile corresponds to the value where the lower tail probability is 0.25 (\( P(Z \leq z) = 0.25 \)).
- The median (50th percentile) corresponds to a lower tail probability of 0.5 (\( P(Z \leq z) = 0.5 \)).
To compute the Z-score corresponding to a given lower tail probability:
from scipy.stats import norm
# Lower tail probability (25th percentile)
p = 0.25
# Z-score for the lower tail probability
z_score = norm.ppf(p)
print(f"Z-Score for lower tail probability of 0.25: {z_score}")
4. Confidence Intervals
In confidence interval calculations, the lower tail probability is used to determine critical values. For example, in a 95% confidence interval, the lower bound may correspond to the 2.5th percentile (\( P(Z \leq z) = 0.025 \)).
5. Quality Control
In quality control or process monitoring, lower tail probabilities can help detect measurements significantly below the mean, such as identifying underfilled products in manufacturing or detecting anomalies in data.
When to Use Upper Tail vs. Lower Tail
- Upper Tail (\( P(Z > z) \)): Used in right-tailed tests or for identifying extreme values above the mean.
- Lower Tail (\( P(Z \leq z) \)): Used in left-tailed tests, percentile calculations, or identifying extreme values below the mean.
By understanding the context of the problem or hypothesis, you can determine whether the lower tail probability is required for your analysis.
Visualizing the One-Tailed and Two-Tailed Tests
Plotting the one-tailed and two-tailed tests helps visualize the Z-score and its associated p-value on the standard normal distribution. Below, we’ll use Python to create a figure with two subplots: one for the one-tailed test and another for the two-tailed test.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters
z_score = 2.5
x = np.linspace(-4, 4, 1000)
y = norm.pdf(x)
# One-tailed p-value
p_value_one_tailed = norm.sf(z_score)
# Two-tailed p-value
p_value_two_tailed = 2 * norm.sf(abs(z_score))
# Plot
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# One-tailed plot
axes[0].plot(x, y, label="Standard Normal Curve", color='black')
axes[0].fill_between(x, y, where=(x >= z_score), color='purple', alpha=0.5, label=f"P-value = {p_value_one_tailed:.4f}")
axes[0].axvline(z_score, color='red', linestyle='--', label=f"Z = {z_score}")
axes[0].set_title("One-Tailed Test")
axes[0].set_xlabel("Z-Score")
axes[0].set_ylabel("Probability Density")
axes[0].legend()
# Two-tailed plot
axes[1].plot(x, y, label="Standard Normal Curve", color='black')
axes[1].fill_between(x, y, where=(x >= z_score), color='purple', alpha=0.5)
axes[1].fill_between(x, y, where=(x <= -z_score), color='purple', alpha=0.5, label=f"P-value = {p_value_two_tailed:.4f}")
axes[1].axvline(z_score, color='red', linestyle='--', label=f"Z = ±{z_score}")
axes[1].axvline(-z_score, color='red', linestyle='--')
axes[1].set_title("Two-Tailed Test")
axes[1].set_xlabel("Z-Score")
axes[1].set_ylabel("Probability Density")
axes[1].legend()
# Display
plt.tight_layout()
plt.show()
Explanation of the Code
- Data Preparation: We generate \( x \)-values ranging from -4 to 4 and calculate the corresponding \( y \)-values using the probability density function (PDF) of the normal distribution.
- One-Tailed Test: The shaded area to the right of the Z-score represents the p-value for the one-tailed test.
- Two-Tailed Test: The shaded areas on both ends of the distribution (beyond \( Z \) and \(-Z\)) represent the p-value for the two-tailed test.
- Subplots: The figure contains two subplots to compare the one-tailed and two-tailed visualizations side by side.
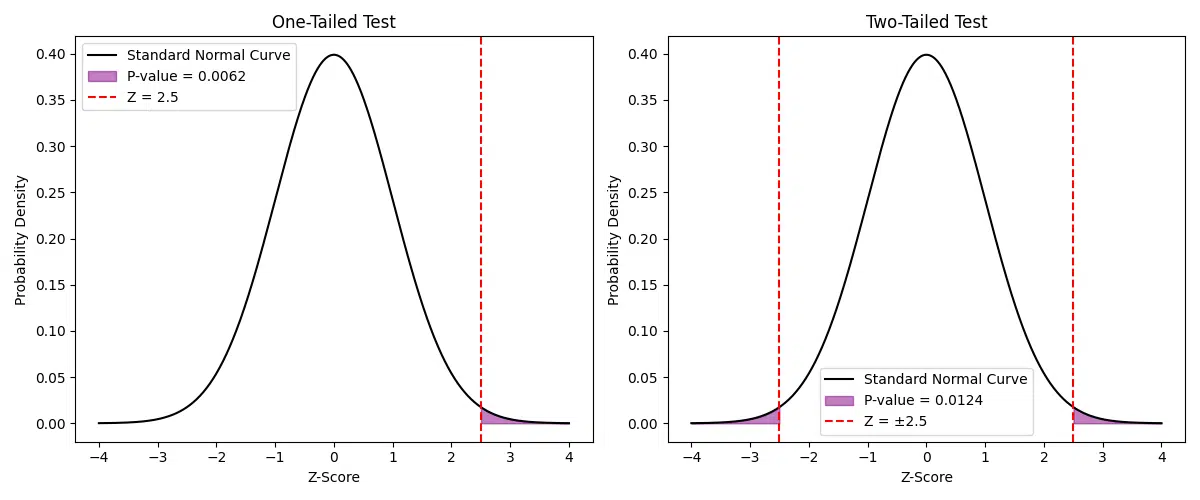
These plots provide a clear understanding of how the Z-score relates to the p-value and the areas under the normal distribution curve.
Assumptions and Limitations of Using Z-Scores and P-Values
Calculating a p-value from a Z-score relies on certain assumptions and has inherent limitations. Here’s what to keep in mind:
Assumptions
- Normality of Data: Z-scores are based on the assumption that the data follows a normal distribution. For smaller datasets, deviations from normality can lead to inaccurate p-values.
- Independent Observations: The data points are assumed to be independent. Violations of this assumption, such as correlated data, can affect the validity of the results.
- Interval or Ratio Scale: Z-scores require data measured on an interval or ratio scale, as they rely on meaningful distances between values. Ordinal or nominal data are not suitable for Z-scores.
- Sufficient Sample Size: For small sample sizes, the standard error may not accurately reflect the population standard deviation, making Z-scores less reliable. Larger sample sizes help stabilize the results due to the Central Limit Theorem.
Limitations
- Sensitivity to Outliers: Z-scores are highly sensitive to outliers, as extreme values can disproportionately affect the mean and standard deviation, leading to misleading results.
- Over-reliance on P-Values: A small p-value indicates statistical significance but does not imply practical significance. It is essential to consider the effect size and context of the findings.
- Multiple Comparisons: Conducting multiple tests on the same dataset increases the likelihood of false positives (Type I errors). Adjustments, like the Bonferroni correction, are necessary to control for this issue.
- Sample Size Effects: In very large samples, even small deviations from the mean can result in statistically significant p-values, potentially overstating their importance. Conversely, small samples may fail to detect meaningful effects, increasing the risk of Type II errors.
- Assumption of a Standard Normal Distribution: The calculation assumes that the standard deviation is known and the data perfectly fits a standard normal distribution. In practice, deviations from this idealized model can reduce accuracy.
By being aware of these assumptions and limitations, you can interpret Z-scores and p-values more effectively, ensuring that your conclusions are based on sound statistical reasoning and appropriate methodologies.
Conclusion
Calculating the p-value from a Z-score in Python is straightforward with the scipy.stats.norm functions, allowing for efficient statistical tests and hypothesis evaluations. By understanding the concepts of one-tailed and two-tailed p-values, you can interpret your results with confidence and determine whether observed values significantly deviate from expectations under the null hypothesis.
This approach makes it easy to compute p-values for Z-scores in any hypothesis testing scenario, empowering you to make clear, evidence-based decisions in your statistical analyses.
Try the Z-Score to P-Value Calculator
Need a quick way to calculate the p-value from a Z-score for your own data? Check out our Z-Score to P-Value Calculator on the Research Scientist Pod.
Happy coding and happy researching!
Suf is a senior advisor in data science with deep expertise in Natural Language Processing, Complex Networks, and Anomaly Detection. Formerly a postdoctoral research fellow, he applied advanced physics techniques to tackle real-world, data-heavy industry challenges. Before that, he was a particle physicist at the ATLAS Experiment of the Large Hadron Collider. Now, he’s focused on bringing more fun and curiosity to the world of science and research online.

