How to Calculate and Report Cronbach’s Alpha in Python with Practical Examples

by Suf | Python, Statistics

Cronbach’s alpha is a crucial measure of internal consistency reliability in psychological and educational research. This comprehensive guide will walk you through calculating and reporting Cronbach’s alpha using Python, complete with practical examples and visualization techniques.

What is Cronbach’s Alpha?
Python Implementation
Basic Scale Analysis
Using Pingouin
Visualizing Results
Item Analysis
Multiple Subscales Analysis
Interpretation Guidelines
Limitations and Considerations
Conclusion
Further Reading
Attribution and Citation

What is Cronbach’s Alpha?

Cronbach’s alpha is mathematically defined as:

\[ \alpha = \frac{k}{k-1}(1-\frac{\sum_{i=1}^k \sigma^2_i}{\sigma^2_t}) \]

📝 Intuitive Understanding: Think of Cronbach’s alpha like measuring the harmony in an orchestra:

High alpha (near 1): Every instrument contributes to the same melody – your scale items work together perfectly
Low alpha (near 0): Each instrument plays its own tune – your items aren’t measuring the same thing

Python Implementation of Cronbach’s Alpha

Before using external libraries like Pingouin, it’s valuable to understand how to implement Cronbach’s alpha from scratch using Python’s scientific computing libraries. This implementation helps understand the underlying calculations and provides flexibility for custom modifications.

Key Components:

Item Variances: The variability of responses for each individual item
Total Variance: The variability of the sum scores across all items
Number of Items: The total number of questions or items in the scale

Basic Cronbach’s Alpha Function

import numpy as np
import pandas as pd
from scipy import stats

def cronbach_alpha(data):
    """
    Calculate Cronbach's alpha for a set of items

    Parameters:
    data (DataFrame): DataFrame where each column is an item

    Returns:
    float: Cronbach's alpha coefficient
    """
    # Convert to numpy array if DataFrame
    if isinstance(data, pd.DataFrame):
        data = data.to_numpy()

    # Number of items
    n_items = data.shape[1]

    # Calculate item variances
    item_variances = np.var(data, axis=0, ddof=1)

    # Calculate total variance
    total_variance = np.var(np.sum(data, axis=1), ddof=1)

    # Calculate Cronbach's alpha
    alpha = (n_items / (n_items - 1)) * (1 - np.sum(item_variances) / total_variance)

    return alpha

Code Breakdown:

Data Handling: The function accepts either a pandas DataFrame or numpy array, converting to numpy for calculations
Variance Calculations:
- item_variances: Calculates variance for each column (item)
- total_variance: Calculates variance of row sums (total scores)
Alpha Calculation: Implements the formula using array operations

Usage Example:

# Example usage with sample data
satisfaction_data = pd.DataFrame({
    'q1': [5, 4, 5, 4, 3],
    'q2': [4, 4, 5, 3, 3],
    'q3': [5, 3, 4, 4, 3]
})

alpha = cronbach_alpha(satisfaction_data)
print(f"Cronbach's alpha: {alpha:.3f}")

Cronbach’s alpha: 0.830

Important Notes:

The function uses ddof=1 for sample variance calculation (N-1 denominator)
The implementation assumes no missing values in the data
All items should be coded in the same direction (reverse coding should be done before analysis)
The function works with any number of items (k≥2)

Basic Scale Analysis

Let’s work through a practical example using a hypothetical satisfaction survey with five items. This example demonstrates how to structure your data, calculate reliability, and interpret the results.

Understanding the Data Structure

Our sample data represents a satisfaction survey where:

Each row represents one respondent
Each column (q1-q5) represents a different survey item
Responses use a 5-point scale (1 = lowest, 5 = highest)
We have 10 respondents in total

Creating and Analyzing Sample Data

import pandas as pd
import numpy as np

# Create sample satisfaction survey data
data = pd.DataFrame({
    'q1': [5, 4, 5, 4, 3, 2, 4, 5, 4, 3],  # Overall satisfaction
    'q2': [4, 4, 5, 3, 3, 2, 5, 4, 4, 3],  # Service quality
    'q3': [5, 3, 4, 4, 3, 1, 4, 5, 4, 2],  # Product quality
    'q4': [4, 4, 4, 3, 3, 2, 4, 4, 3, 3],  # Value for money
    'q5': [5, 4, 5, 4, 2, 2, 5, 5, 4, 3]   # Likelihood to recommend
})

# Calculate Cronbach's alpha
alpha = cronbach_alpha(data)
print(f"Cronbach's alpha: {alpha:.3f}")

Cronbach’s alpha: 0.952

Interpreting the Results

Our analysis shows α = 0.952, which indicates:

Excellent Internal Consistency: Well above the common threshold of 0.70
Strong Item Relationships: The items are measuring the same underlying construct
Potential Item Redundancy: Values above 0.90 might suggest some items are too similar

Code Breakdown:

Data Creation:
- Using pandas DataFrame for structured data storage
- Each question stored as a separate column
- Data represents realistic survey responses
Analysis:
- Direct application of our cronbach_alpha function
- Result formatted to three decimal places

Practical Considerations:

Ensure all items are coded in the same direction before analysis
Check for missing values in your dataset
Consider your sample size (n=10 is small for actual research)
For high alpha values (>0.90), review items for potential redundancy

Visualizing Results

Visualization helps identify patterns in item relationships and potential scale issues. A correlation heatmap is particularly useful for examining internal consistency.

Creating a Correlation Heatmap

import seaborn as sns
import matplotlib.pyplot as plt

# Calculate correlation matrix
corr_matrix = data.corr()

# Create heatmap
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix,
            annot=True,         # Show correlation values
            cmap='RdBu_r',      # Color scheme: red-blue reversed
            vmin=-1,            # Minimum correlation value
            vmax=1,             # Maximum correlation value
            center=0)           # Center point for color scheme
plt.title('Item Correlation Matrix')
plt.show()

Code Components:

data.corr(): Calculates Pearson correlations between all items
cmap=’RdBu_r’: Red for positive, blue for negative correlations
annot=True: Displays numerical correlation values
center=0: Centers color scale at zero correlation

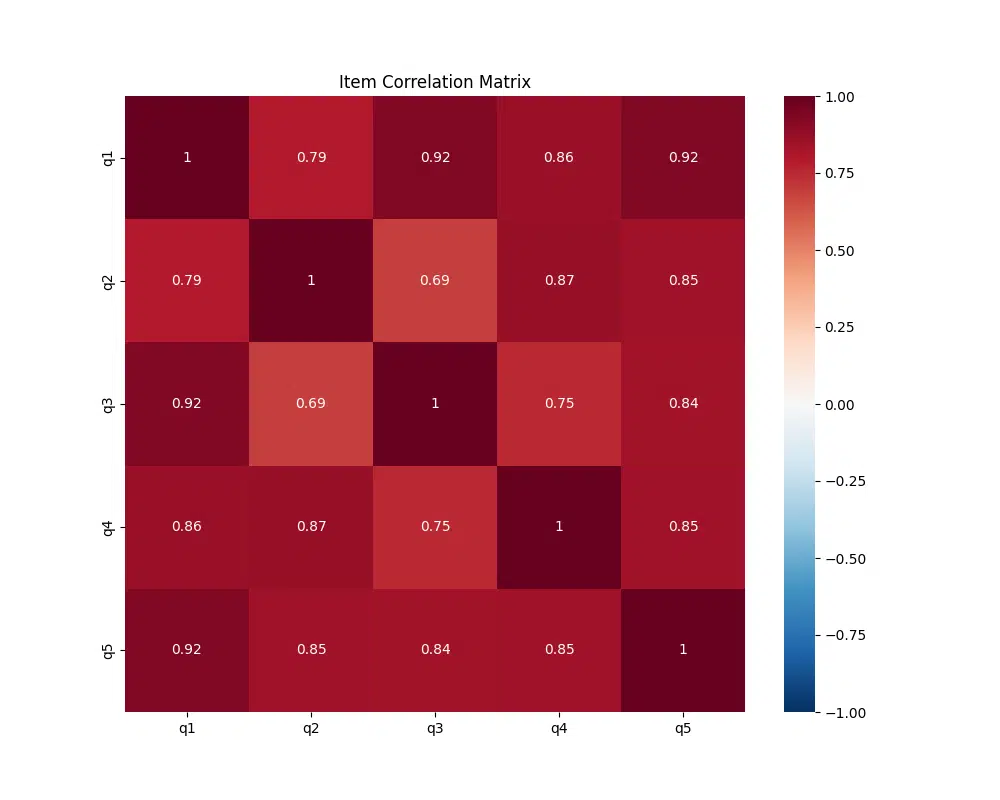
Correlation heatmap visualizing relationships between scale items. The heatmap shows a 5x5 matrix with cells colored from dark red (strong positive correlations) to white (neutral) to dark blue (negative correlations). Each cell displays the numerical correlation value. The diagonal shows perfect 1.0 correlations in dark red, while off-diagonal elements show varying degrees of positive correlations ranging from 0.69 to 0.92, indicating strong internal consistency. — Item Correlation Matrix: The heatmap displays strong positive correlations (red) between all items, suggesting high reliability but potential redundancy. The correlation values range from 0.69 to 0.92, with perfect correlations (1.0) along the diagonal. This pattern indicates excellent internal consistency (α = 0.952) but may suggest some items are measuring the same aspect of the construct.

Reading the Heatmap:

Color Intensity: Darker red indicates stronger positive correlations
Diagonal: Always 1.0 (self-correlation)
Ideal Pattern: Moderate to strong positive correlations (0.3 to 0.7)
Warning Signs:
- Very high correlations (>0.9): Potential redundancy
- Low correlations (<0.3): Possible item misfit
- Negative correlations: Potential reverse coding issues

Using Pingouin for Cronbach’s Alpha Calculation

While we can calculate Cronbach’s alpha using NumPy and Pandas as shown above, the Pingouin library offers a more streamlined approach with built-in confidence intervals. This statistical library is particularly useful for psychological research and provides a straightforward way to assess scale reliability.

Installing and Using Pingouin

# First, install Pingouin if you haven't already
# pip install pingouin

import pingouin as pg
import pandas as pd

# Create sample data for a satisfaction survey
data = pd.DataFrame({
    'q1': [5, 4, 5, 4, 3, 2, 4, 5, 4, 3],  # Overall satisfaction
    'q2': [4, 4, 5, 3, 3, 2, 5, 4, 4, 3],  # Service quality
    'q3': [5, 3, 4, 4, 3, 1, 4, 5, 4, 2],  # Product quality
    'q4': [4, 4, 4, 3, 3, 2, 4, 4, 3, 3],  # Value for money
    'q5': [5, 4, 5, 4, 2, 2, 5, 5, 4, 3]   # Likelihood to recommend
})

# Calculate Cronbach's alpha with confidence intervals
alpha_result = pg.cronbach_alpha(data)

# Unpack the results
alpha, ci= alpha_result
ci_lower, ci_upper = ci

print("Cronbach's alpha analysis:")
print(f"Alpha coefficient: {alpha:.3f}")
print(f"95% CI: [{ci_lower:.3f}, {ci_upper:.3f}]")

Cronbach’s alpha analysis:
Alpha coefficient: 0.952
95% CI: [0.879, 0.986]

Understanding the Output

The Pingouin function returns two elements:

Alpha Coefficient (0.952): The point estimate of Cronbach’s alpha, indicating excellent internal consistency in our example.
95% Confidence Interval [0.879, 0.986]: We can be 95% confident that the true alpha falls between these values. The wider interval (compared to the previous example) suggests more uncertainty in our estimate, possibly due to sample size or response variability.

The confidence interval width (0.107) indicates moderate precision in our alpha estimate. Larger sample sizes typically yield narrower intervals.

Reporting Results from Pingouin

When writing up your results using Pingouin’s output, you should include both the alpha coefficient and its confidence interval. Here’s an example of how to report these findings in a research paper:

“The satisfaction scale demonstrated excellent internal consistency reliability (Cronbach’s α = .952, 95% CI [.879, .986]). The moderately wide confidence interval suggests some uncertainty in the reliability estimate, possibly due to sample size.”

Remember that while Pingouin makes it easy to calculate Cronbach’s alpha, you should still consider the assumptions and limitations discussed earlier in this guide. A high alpha coefficient (like 0.952 in our example) might indicate excellent reliability, but it could also suggest item redundancy if it’s much above 0.90.

Visualizing Reliability Analysis Results

While Pingouin does not include built-in visualization tools, we can create informative visualizations of our reliability analysis by combining Pingouin’s calculations with plotting libraries like seaborn and matplotlib. These visualizations can help us better understand our scale’s reliability and item relationships.

Creating a Correlation Heatmap with Confidence Intervals

import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
import pingouin as pg

# Calculate correlations with confidence intervals using Pingouin
def create_correlation_heatmap_with_ci(data):
    # Get the number of items
    n_items = len(data.columns)

    # Create matrices for correlations and CIs
    correlations = np.zeros((n_items, n_items))
    ci_lower = np.zeros((n_items, n_items))
    ci_upper = np.zeros((n_items, n_items))

    # Calculate correlations and CIs for each pair
    for i, col1 in enumerate(data.columns):
        for j, col2 in enumerate(data.columns):
            if i <= j:  # Only calculate upper triangle
                corr_result = pg.corr(data[col1], data[col2], method='pearson')
                correlations[i, j] = corr_result['r'].values[0]
                ci_lower[i, j] = corr_result['CI95%'].values[0][0]
                ci_upper[i, j] = corr_result['CI95%'].values[0][1]

                # Mirror the values for lower triangle
                if i != j:
                    correlations[j, i] = correlations[i, j]
                    ci_lower[j, i] = ci_lower[i, j]
                    ci_upper[j, i] = ci_upper[i, j]

    # Create the heatmap
    plt.figure(figsize=(10, 8))
    sns.heatmap(correlations,
                annot=True,
                cmap='RdBu_r',
                vmin=-1,
                vmax=1,
                center=0,
                fmt='.2f')

    plt.title('Item Correlation Matrix with Confidence Intervals')
    plt.tight_layout()

    return correlations, ci_lower, ci_upper

# Apply to our data
correlations, ci_lower, ci_upper = create_correlation_heatmap_with_ci(data)
plt.show()

# Print confidence intervals
print("\nCorrelation Confidence Intervals:")
for i, item1 in enumerate(data.columns):
    for j, item2 in enumerate(data.columns):
        if i < j:  # Only print upper triangle
            print(f"{item1}-{item2}: {correlations[i,j]:.2f} [95% CI: {ci_lower[i,j]:.2f}, {ci_upper[i,j]:.2f}]")

When we run this visualization code, it will produce the same correlation matrix heatmap as before, showing the strength of relationships between items. Additionally, we now calculate and display confidence intervals for each correlation, providing insight into the precision of our correlation estimates.

Correlation Confidence Intervals:
q1-q2: 0.79 [95% CI: 0.32, 0.95]
q1-q3: 0.92 [95% CI: 0.70, 0.98]
q1-q4: 0.86 [95% CI: 0.51, 0.97]
q1-q5: 0.92 [95% CI: 0.70, 0.98]
q2-q3: 0.69 [95% CI: 0.11, 0.92]
q2-q4: 0.87 [95% CI: 0.53, 0.97]
q2-q5: 0.85 [95% CI: 0.48, 0.96]
q3-q4: 0.75 [95% CI: 0.23, 0.94]
q3-q5: 0.84 [95% CI: 0.45, 0.96]
q4-q5: 0.85 [95% CI: 0.47, 0.96]

Looking at the confidence intervals in the output:

All correlations are strong (>0.69) with the strongest between q1-q3 and q1-q5 (both 0.92)
The confidence intervals are relatively wide (most spanning around 0.4-0.5 units), indicating some uncertainty in the exact correlation values
Even at the lower bounds of the CIs, most correlations remain moderate to strong (>0.3)
The width of these intervals suggests our sample size may be limiting precision
No confidence interval includes zero, supporting the statistical significance of all item correlations

This additional information helps us understand not just the strength of item relationships, but also how confident we can be in these estimates.

Creating a Reliability Profile Plot

Understanding Reliability Profiles

A reliability profile plot provides three key insights:

Response Patterns: Mean scores for each item show if certain questions consistently receive higher or lower ratings
Measurement Precision: Confidence intervals indicate how precisely we can estimate the true item means
Scale Consistency: The overall pattern helps identify items that may be performing differently from others

Creating a Reliability Profile Plot

def plot_reliability_profile(data):
    """Create a profile plot showing item means and their 95% confidence intervals"""
    means = data.mean()
    sems = data.sem()  # Standard error of the mean

    # Calculate 95% confidence intervals
    ci = sems * 1.96

    plt.figure(figsize=(10, 6))

    # Plot means with error bars
    plt.errorbar(range(len(means)), means, yerr=ci, fmt='o', capsize=5)

    # Customize the plot
    plt.xlabel('Scale Items')
    plt.ylabel('Mean Score')
    plt.title('Item Response Profile with 95% Confidence Intervals')
    plt.xticks(range(len(means)), data.columns)
    plt.grid(True, linestyle='--', alpha=0.7)

    # Add horizontal line at the scale midpoint
    plt.axhline(y=np.mean([data.min().min(), data.max().max()]),
                color='gray',
                linestyle='--',
                alpha=0.5)

    plt.tight_layout()
    plt.show()

# Create the reliability profile plot
plot_reliability_profile(data)

Statistical Components

Standard Error of Mean (SEM): Estimates the standard deviation of sample means
Confidence Intervals: Calculated as ±1.96 * SEM for 95% confidence level
Scale Midpoint: Reference line showing the middle of the possible response range

Item Response Profile: The plot shows mean scores (dots) and 95% confidence intervals (error bars) for each scale item. Items above the midpoint (dashed line) indicate higher average ratings, while longer error bars suggest greater response variability.

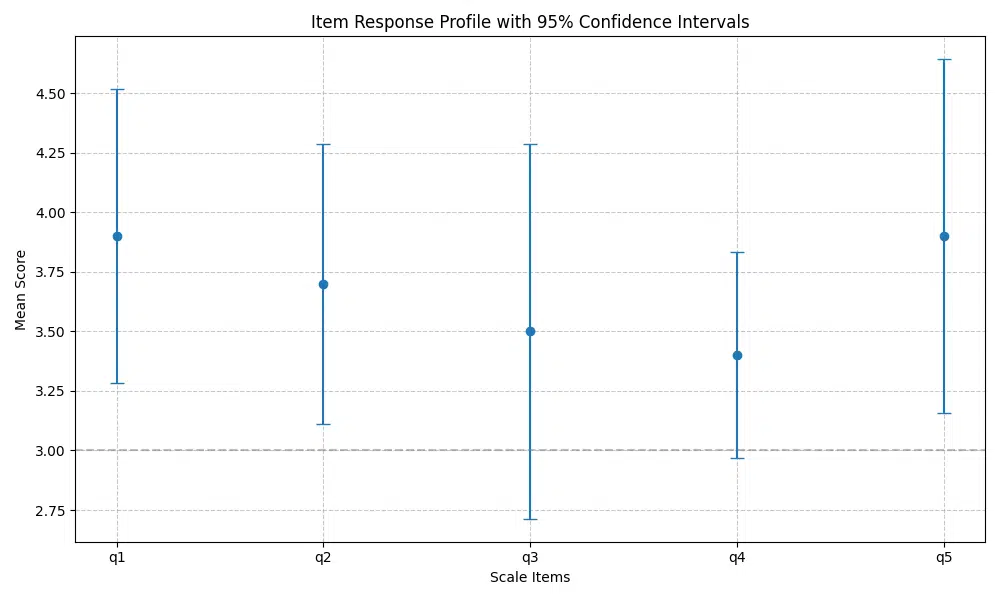
Reading the Profile Plot

Mean Scores: Points above/below the midpoint show items with higher/lower average ratings
Error Bar Size: Longer bars indicate less precise estimates, possibly due to:
- Greater response variability
- Smaller sample size
- Possible item clarity issues
Pattern Analysis:
- Similar means suggest consistent item difficulty
- Overlapping CIs indicate statistically similar responses
- Outlier items may need review or revision

📊 Visualization Best Practices

Always include proper axis labels and titles to make your visualizations self-explanatory
Use color scales that are both informative and accessible (like the RdBu_r colormap used above)
Include confidence intervals to show the precision of your estimates
Consider your audience when deciding how much detail to include in the visualization

Detailed Item Analysis in Python

While Pingouin provides the basic Cronbach's alpha calculation, we can create a more comprehensive item analysis similar to R's psych package. This analysis helps us understand how each item contributes to the scale's reliability and identify potential improvements.

Comprehensive Item Analysis Function

import pandas as pd
import numpy as np
from pingouin import cronbach_alpha

def detailed_item_analysis(data):
    """
    Perform detailed item analysis similar to R's psych package

    Parameters:
    data (pd.DataFrame): DataFrame where each column is a scale item

    Returns:
    tuple: (item_stats, alpha_if_dropped)
    """
    n_items = len(data.columns)
    n_subjects = len(data)

    # Calculate scale statistics
    item_means = data.mean()
    item_sds = data.std()

    # Calculate item-total correlations
    item_stats = {}
    alpha_if_dropped = {}

    for item in data.columns:
        # Calculate total score excluding current item
        rest_score = data.drop(columns=[item]).sum(axis=1)

        # Calculate correlation with total
        item_total_corr = data[item].corr(rest_score)

        # Calculate standardized correlation
        item_std = (data[item] - data[item].mean()) / data[item].std()
        rest_std = (rest_score - rest_score.mean()) / rest_score.std()
        std_corr = np.corrcoef(item_std, rest_std)[0, 1]

        # Calculate alpha if item deleted
        scale_without_item = data.drop(columns=[item])
        alpha_dropped = cronbach_alpha(scale_without_item)[0]

        # Store statistics
        item_stats[item] = {
            'n': n_subjects,
            'mean': item_means[item],
            'sd': item_sds[item],
            'raw_r': item_total_corr,
            'std_r': std_corr
        }

        alpha_if_dropped[item] = alpha_dropped

    return pd.DataFrame(item_stats).T, pd.Series(alpha_if_dropped)

# Create sample data
data = pd.DataFrame({
    'q1': [5, 4, 5, 4, 3, 2, 4, 5, 4, 3],
    'q2': [4, 4, 5, 3, 3, 2, 5, 4, 4, 3],
    'q3': [5, 3, 4, 4, 3, 1, 4, 5, 4, 2],
    'q4': [4, 4, 4, 3, 3, 2, 4, 4, 3, 3],
    'q5': [5, 4, 5, 4, 2, 2, 5, 5, 4, 3]
})

# Perform analysis
item_statistics, alphas_dropped = detailed_item_analysis(data)

# Print results
print("Item Statistics:")
print(item_statistics.round(4))
print("\nAlpha if Item Dropped:")
print(alphas_dropped.round(4))

Item Statistics:
n mean sd raw_r std_r
q1 10.0 3.9 0.9944 0.9536 0.9536
q2 10.0 3.7 0.9487 0.8342 0.8342
q3 10.0 3.5 1.2693 0.8550 0.8550
q4 10.0 3.4 0.6992 0.8836 0.8836
q5 10.0 3.9 1.1972 0.9336 0.9336

Alpha if Item Dropped:
q1 0.9257
q2 0.9460
q3 0.9487
q4 0.9489
q5 0.9294

Understanding the Output

Item-Total Statistics:

n (10 for all items): Number of responses
mean (range 3.4-3.9): Average item scores
sd (range 0.70-1.27): Response variability
raw_r (range 0.83-0.95): Item-total correlations
std_r: Standardized correlations (identical to raw_r in this case)

Analyzing Our Results

Item Performance:

Q1 has the strongest correlation (0.954), indicating best construct measurement
Q2 shows lowest correlation (0.834), still well above acceptable
All correlations >0.83 suggest strong construct cohesion

Response Patterns:

Q1/Q5: Highest means (3.9) - most positively rated
Q4: Lowest mean (3.4), smallest SD (0.70) - consistent, lower ratings
Q3: Highest SD (1.27) - most response variation

Scale Optimization:

All alpha-if-dropped values (0.926-0.949) below overall alpha (0.952)
Q1 removal most impactful (α→0.926)
Q3/Q4 removal least impactful but still worth retaining

Recommendation: Retain all items. While reliability is very high (potentially indicating redundancy), each item shows good psychometric properties.

Analyzing Multiple Subscales

Questionnaires often contain multiple subscales measuring different aspects of a construct. For example, a job satisfaction survey might include:

Work Environment (3 items)
Compensation (3 items)
Professional Growth (3 items)

Multiple Subscales Analysis with Pingouin

import pandas as pd
import pingouin as pg

# Create sample questionnaire data
data = pd.DataFrame({
    # Work Environment subscale
    'env1': [5, 4, 5, 4, 3, 4, 5, 4, 3, 4],
    'env2': [4, 4, 5, 3, 3, 4, 4, 3, 3, 5],
    'env3': [5, 3, 4, 4, 3, 5, 4, 4, 4, 4],

    # Compensation subscale
    'comp1': [3, 2, 4, 3, 2, 3, 4, 3, 2, 3],
    'comp2': [4, 3, 4, 3, 2, 4, 3, 3, 2, 4],
    'comp3': [3, 2, 3, 2, 2, 3, 4, 2, 2, 3],

    # Professional Growth subscale
    'grow1': [4, 5, 4, 3, 4, 5, 4, 4, 3, 4],
    'grow2': [5, 4, 5, 4, 3, 4, 5, 3, 4, 5],
    'grow3': [4, 5, 4, 3, 4, 5, 4, 4, 3, 4]
})

def analyze_subscale(data, subscale_items, name):
    """Analyze a subscale and return formatted results"""
    alpha_result = pg.cronbach_alpha(data[subscale_items])

    # Handle different return formats
    if isinstance(alpha_result[1], np.ndarray):
        # Format: (alpha, array([ci_lower, ci_upper]))
        alpha = alpha_result[0]
        ci_lower, ci_upper = alpha_result[1]
    else:
        # Format: (alpha, ci_lower, ci_upper)
        alpha, ci_lower, ci_upper = alpha_result

    mean = data[subscale_items].mean().mean()
    std = data[subscale_items].mean().std()

    return {
        'Subscale': name,
        'Alpha': round(alpha, 3),
        'CI_lower': round(ci_lower, 3),
        'CI_upper': round(ci_upper, 3),
        'Mean': round(mean, 2),
        'SD': round(std, 2)
    }

# Define subscales
subscales = {
    'Work Environment': ['env1', 'env2', 'env3'],
    'Compensation': ['comp1', 'comp2', 'comp3'],
    'Professional Growth': ['grow1', 'grow2', 'grow3']
}

# Analyze each subscale
results = []
for name, items in subscales.items():
    results.append(analyze_subscale(data, items, name))

# Create results dataframe
results_df = pd.DataFrame(results)
print(results_df)

Subscale Alpha CI_lower CI_upper Mean SD
0 Work Environment 0.691 0.096 0.917 3.97 0.15
1 Compensation 0.845 0.545 0.958 2.90 0.30
2 Professional Growth 0.556 -0.302 0.880 4.07 0.12

Subscale Analysis Results

Work Environment (α = 0.691)

Questionable reliability (α < 0.7)
Wide CI [0.096, 0.917] indicates uncertainty
High mean (3.97) suggests positive perceptions

Compensation (α = 0.845)

Good reliability
More precise CI [0.545, 0.958]
Lowest mean (2.90) indicates less satisfaction

Professional Growth (α = 0.556)

Poor reliability (α < 0.6)
Very wide CI [0, 0.880] indicates poor measurement precision
Highest mean (4.07) but unreliable measurement
Consider scale revision and larger sample size

Recommendations

Only Compensation subscale meets reliability standards
Professional Growth items need significant revision
Work Environment scale needs minor improvements
Consider increasing sample size to improve precision

Additional Considerations

Check for correlations between subscales to ensure distinctness
Consider the impact of subscale length on reliability
Review items in subscales with lower reliability
Use confidence intervals to assess estimate precision

Interpretation Guidelines

Cronbach's Alpha Range	Interpretation	Recommended Action
α ≥ 0.9	Excellent	Consider item redundancy if > 0.95
0.8 ≤ α < 0.9	Good	Suitable for research purposes
0.7 ≤ α < 0.8	Acceptable	Consider item improvement
0.6 ≤ α < 0.7	Questionable	Review and revise scale
α < 0.6	Poor	Major revision needed

Limitations and Considerations

When using Cronbach's alpha in Python, keep these important considerations in mind:

Sample Size: Larger samples (n > 300) provide more stable estimates
Missing Data: Handle missing values appropriately before analysis
Assumptions: Check for unidimensionality and tau-equivalence
Scale Length: Alpha tends to increase with more items

Conclusion

Cronbach's alpha is a fundamental tool for assessing scale reliability, and Python offers multiple approaches for its calculation and interpretation. Essential practices:

Calculate confidence intervals with Pingouin to assess precision
Examine item-total correlations for scale refinement
Consider alpha-if-item-deleted values for optimization
Report both overall alpha and subscale reliability
Interpret results within sample size constraints

Remember that while high alpha values indicate reliability, they may also suggest item redundancy. Always interpret Cronbach's alpha alongside other psychometric evidence. For comparison, see how to calculate and report Cronbach's alpha in R.

Attribution and Citation

If you found this guide and tools helpful, feel free to link back to this page or cite it in your work!

Suf

Senior Advisor, Data Science | [email protected] | + posts

Suf is a senior advisor in data science with deep expertise in Natural Language Processing, Complex Networks, and Anomaly Detection. Formerly a postdoctoral research fellow, he applied advanced physics techniques to tackle real-world, data-heavy industry challenges. Before that, he was a particle physicist at the ATLAS Experiment of the Large Hadron Collider. Now, he’s focused on bringing more fun and curiosity to the world of science and research online.

Buy Me a Coffee ✨

How to Calculate and Report Cronbach’s Alpha in Python with Practical Examples

Table of Contents

What is Cronbach’s Alpha?

Python Implementation of Cronbach’s Alpha

Key Components:

Code Breakdown:

Usage Example:

Important Notes:

Basic Scale Analysis

Understanding the Data Structure

Interpreting the Results

Code Breakdown:

Practical Considerations:

Visualizing Results

Code Components:

Reading the Heatmap:

Using Pingouin for Cronbach’s Alpha Calculation

Reporting Results from Pingouin

Visualizing Reliability Analysis Results

Creating a Reliability Profile Plot

Understanding Reliability Profiles

Statistical Components

Reading the Profile Plot

Detailed Item Analysis in Python

Understanding the Output

Item-Total Statistics:

Analyzing Our Results

Item Performance:

Response Patterns:

Scale Optimization:

Analyzing Multiple Subscales

Subscale Analysis Results

Work Environment (α = 0.691)

Compensation (α = 0.845)

Professional Growth (α = 0.556)

Recommendations

Additional Considerations

Interpretation Guidelines

Limitations and Considerations

Conclusion

Further Reading

Attribution and Citation

Suf