How to Calculate the Cartesian Product in Python

The Cartesian product of two sets A and B denoted A x B is the set of all possible ordered pairs (a, b), where a is in A and b is in B. We can get the Cartesian product between two lists saved as a 2D list in Python.

This tutorial will go through different methods to get the Cartesian product of two lists.

---

What is the Cartesian Product of Two Sets?

Given two non-empty sets A and B, the Cartesian product A x B is the set of all ordered pairs of the elements from A and B. You can see a visual of the Cartesian product of two sets below.

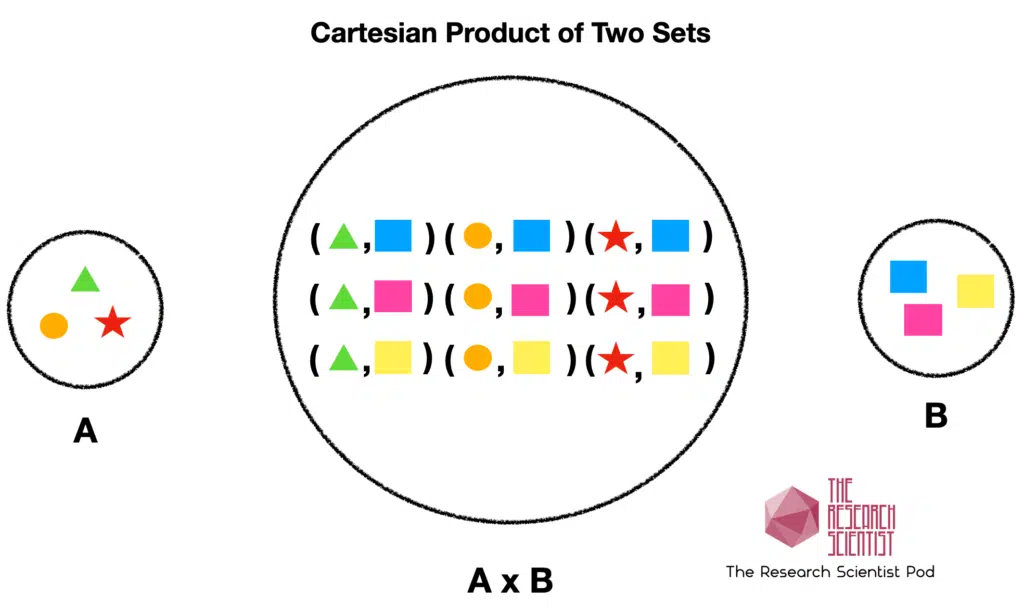
Calculate the Cartesian Product In Python using itertools

We can use the product method from the itertools module to calculate the Cartesian product of two iterable objects. The syntax for the itertools product method is:

product(*iterables, repeat=1)

The function takes two iterables as input and returns their Cartesian product as output in the order of arguments provided. The unpacking operator * unpacks the argument iterables. Let’s look at an example where we calculate the Cartesian product using the itertools.product() method:

from itertools import product

lists = [['a', 'b', 'c'], [1, 2, 3]]

for i in product(*lists):
    print(i)

In the above example, we pass the list variables, which stores two lists, to the product method. Let’s run the code to get the result:

('a', 1)
('a', 2)
('a', 3)
('b', 1)
('b', 2)
('b', 3)
('c', 1)
('c', 2)
('c', 3)

In this example, we calculated the Cartesian product of two lists, but we can use the product method to calculate the product for more than two lists. Let’s look at an example, with three lists

from itertools import product

lists = [['a', 'b', 'c'], [1, 2, 3], [x, y, z]]

for i in product(*lists):
    print(i)

Let’s run the code to get the result:

('a', 1, 'x')
('a', 1, 'y')
('a', 1, 'z')
('a', 2, 'x')
('a', 2, 'y')
('a', 2, 'z')
('a', 3, 'x')
('a', 3, 'y')
('a', 3, 'z')
('b', 1, 'x')
('b', 1, 'y')
('b', 1, 'z')
('b', 2, 'x')
('b', 2, 'y')
('b', 2, 'z')
('b', 3, 'x')
('b', 3, 'y')
('b', 3, 'z')
('c', 1, 'x')
('c', 1, 'y')
('c', 1, 'z')
('c', 2, 'x')
('c', 2, 'y')
('c', 2, 'z')
('c', 3, 'x')
('c', 3, 'y')
('c', 3, 'z')

Calculate the Cartesian Product In Python using List Comprehension

We can use the list comprehension method to get the Cartesian product of the lists if we know the total number of lists. If we know the number of lists, we can iterate through each element in each list using the for loop to get the Cartesian product.

Let’s look at an example of using the list comprehension method to calculate the Cartesian product of two lists.

lists = [['a', 'b', 'c'], [1, 2, 3]]

cartesian_product = [(x,y) for x in lists[0] for y in lists[1]]

print(cartesian_product)

Let’s run the code to get the output:

[('a', 1), ('a', 2), ('a', 3), ('b', 1), ('b', 2), ('b', 3), ('c', 1), ('c', 2), ('c', 3)]

Calculate the Cartesian Product in Python using the Iterative Method

We can use an iterative method as an alternative to the list comprehension approach. In this case, we do not need to have a fixed number of lists or sets for the Cartesian product.

def cartesian_product_func(lists):

    result = [[]]

    for list_ in lists:

        result = [x+[y] for x in result for y in list_]

    return result

lists = [['a', 'b', 'c'], [1, 2, 3]]

print(cartesian_product_func(lists))

Let’s run the code to see the output:

[['a', 1], ['a', 2], ['a', 3], ['b', 1], ['b', 2], ['b', 3], ['c', 1], ['c', 2], ['c', 3]]

Summary

Congratulations on reading to the end of this tutorial! We have gone through several methods to get the Cartesian product between lists in Python. The itertools.product() method is the most straightforward approach as it only requires you to import the itertools module to call the method. The product method and the iterative method can accept any number of lists. The list comprehension requires a predetermined number of lists or sets to calculate the Cartesian product.

Go to the online courses page on Python to learn more about Python for data science and machine learning.

Have fun and happy researching!