Hamming distance is a type of string metric for finding how similar two binary data strings are. If the strings are equal in length, Hamming distance determines the number of bit positions different between them. We can also describe Hamming distance as the minimum number of substitutions required to change one string into another or the minimum number of errors that transform one string to another. In this article, we will go through examples of Hamming distance using Python and applications of Hamming Distance across multiple disciplines.
Table of contents
Visual Description of Hamming Distance
Let’s look at an example of calculating the Hamming distance between two DNA sequences:

There are edits at two locations between the two strings, and therefore the Hamming distance is 2.
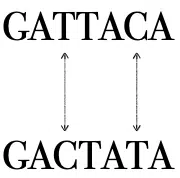
The Hamming distance applies to any string, not just DNA sequences. Calculating the Hamming distance by hand can be time-consuming once strings become hundreds or thousands of characters long.
For ease and speed, we can calculate the Hamming distance programmatically.
Calculating the Hamming Distance Between Two Bit Strings
In data science, you may encounter bitstrings when dealing with one-hot encoded categorical columns of data. To calculate the Hamming distance between bitstrings, we sum the differences between the strings, which will always be 0 or 1, then normalize the value by dividing by the length of the bitstrings. Let’s look at making a Hamming distance function and apply it to two bitstrings.
# Manually calculating the Hamming distance between two bit strings
# Custom function
def hamming_distance(a, b):
# Determine if strings are equal in length
if len(a) != len(b):
print('String are not equal in length')
else:
return sum(abs(e1 - e2) for e1, e2 in zip(a, b))/ len(a)
# Input data
bit_1 = [0, 0, 1, 0, 1, 0]
bit_2 = [0, 0, 0, 1, 0, 0]
# Calculate distance
dist = hamming_distance(bit_1, bit_2)
# Print result
print(dist)
0.5
We can see by eye that there are three differences between the bitstrings, or three out of the six-bit positions are different. When averaged over the length of the bitstrings (3 / 6 ), the Hamming distance is 0.5.
Python has many scientific computing libraries that provide distance metric functions. Let’s look at an example of using SciPy to calculate the Hamming distance between the same bitstrings in the manual example.
# Calculating Hamming distance between bit strings using SciPy # Get Hamming function from scipy.spatial.distance import hamming # Calculate Hamming distance dist = hamming(bit_1, bit_2) # Print result print(dist)
0.5
Running the code, we can see we obtain the same result as the manual implementation of 0.5.
The History of the Hamming Distance
Richard Hamming invited the Hamming distance, an American mathematician, who programmed IBM calculating machines for the Manhattan project. He moved to Bell Laboratories from the Manhattan Project and developed the Hamming distance, which has profound implications for the fields of computer science and telecommunications.
In 1950, Hamming published a paper that postulated it could detect and correct errors in bit strings by calculating the number of disparate bits between valid and erroneous code, which became known as the Hamming distance.
The Hamming Weight
The Hamming weight is the Hamming distance from the zero string, a string consisting of all zeros of the same length as the selected string. In other words, it is the number of elements in the string that are not zero. This value would be the number of 1’s present in the string for a binary string. For example, the Hamming weight of 101011 is 4. The hamming weight is also called the population count, popcount, sideways sum, or bit summation.
Metric Space using Hamming Distance
The metric space of length-n binary strings, using the Hamming distance, is known as the Hamming cube and is equivalent as a metric space to the set of distances between vertices in a hypercube graph.
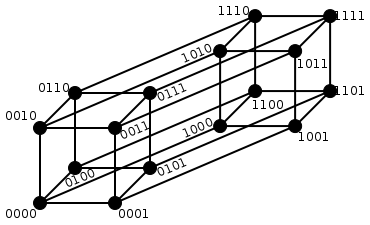
We can view a binary string of length n as a vector in $latex \mathbb{R}^{n}$, where each character or symbol in the string is a coordinate. The strings form the vertices of an n-dimensional hypercube, and the Hamming distance of the strings is equivalent to the Manhattan distance between the vertices.
Limitations of Hamming Distance
For comparing strings that are different lengths, or strings where not just substitutions but also insertions or deletions can occur, we can use the Levenshtein distance.
Applications of Hamming Distance
Hamming distance has several applications, including:
- Block code in coding theory, where block code may refer to any error-correcting code that acts on a block of k bits of input data to produce n bits of output data.
- Automatic spelling correction can determine candidate corrections for a misspelt word by selecting words from a dictionary that have a low Hamming distance from the misspelt word.
- In bioinformatics, we can use the Hamming distance to quantify the similarity between DNA sequences, which we can represent as strings of the characters A, C, G, and T.
- In telecommunication, Hamming distance is used to count the number of flipped bits in a fixed-length binary word as an estimation of error. This is called the signal distance.
- Machine learning like semi-supervised clustering, nearest neighbor classification, and kernel-based methods require the existence of a pairwise similarity measure on the input space. The Hamming distance provides a natural similarity measure between binary codes and can be computed with a few machine instructions per comparison. The exact nearest neighbor search in Hamming space is significantly faster than linear search, with sublinear run-times.
- Employing Hamming distance-based test statistics for studies concerning population heterogeneity.
Summary
Congratulations on reading to the end of this article!
You know the Hamming distance, its appropriate use, and how to manually calculate it in Python and by importing SciPy.
The Hamming distance between two strings of equal length is the minimum number of edits required to turn one string into another.
The Hamming distance has limitations; it does not apply to bitstrings of different lengths, in which case we can use the Levenshtein distance.
Hamming distance has many applications in multiple disciplines and is suitable for vast datasets with interpretable results.
To calculate the Hamming distance in R, go to the article: How to Calculate the Hamming Distance in R.
To calculate the Hamming distance in C++, go to the article: How to Calculate Hamming Distance in C++ (With C++20, Bit Shifting, Strings, and More).
You can go to the article on Cosine Similarity and Jaccard Similarity for more on similarity measures.
Go to our guide: Levenshtein Distance: A Comprehensive Guide for In-depth Explanation of Levenshtein Distance, its algorithm, properties, and Applications in string edit Distance.
Go to our guide, Damerau-Levenshtein Distance: A Guide to String Similarity with Transpositions, for an in-depth explanation of Levenshtein Distance, its algorithm, properties, and Applications in string edit Distance.
Have fun and happy researching!
Suf is a senior advisor in data science with deep expertise in Natural Language Processing, Complex Networks, and Anomaly Detection. Formerly a postdoctoral research fellow, he applied advanced physics techniques to tackle real-world, data-heavy industry challenges. Before that, he was a particle physicist at the ATLAS Experiment of the Large Hadron Collider. Now, he’s focused on bringing more fun and curiosity to the world of science and research online.

