How to Do Bubble Sort in Python

Bubble sort is a popular sorting algorithm that compares the adjacent elements in a list and swaps them if they are not in the specified order.

This tutorial will go through how to implement the bubble sort algorithm in Python with the help of code examples.

---

How Bubble Sort Works

The bubble sort algorithm, also known as sinking sort, is the most straightforward sorting algorithm. The algorithm goes through an array repeatedly, compares adjacent elements and swaps them if they are out of order. We can use the bubble sort algorithm to sort in ascending (largest element last) or descending order (largest element first). Let’s look at an example of how the bubble sort algorithm can sort an array of five numbers in ascending order.

First Iteration

1. Starting from the first element in the array, compare the first and second elements.
2. If the first element is greater than the second element, swap the elements.
3. Compare the second and third elements, swap them if they are not in order.
4. Proceed with the above process until the last element.

Let’s look at the first pass, which means the algorithm goes over the array:

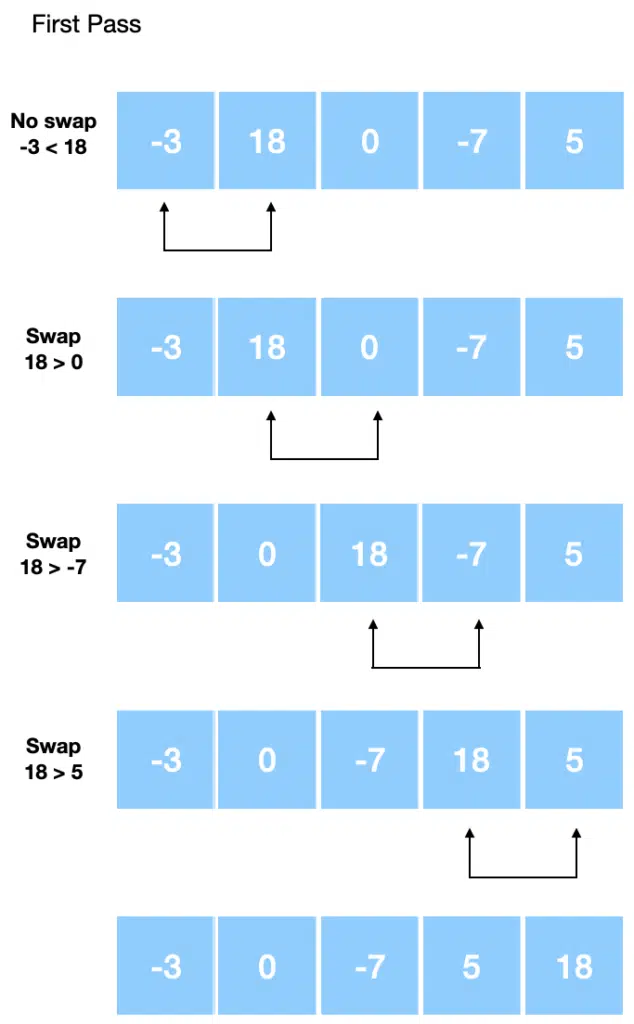
The above image shows how the array looks after each step in the pass over the array. Note how the largest number in the array bubbles to the top of the array. Let’s look at the second pass:

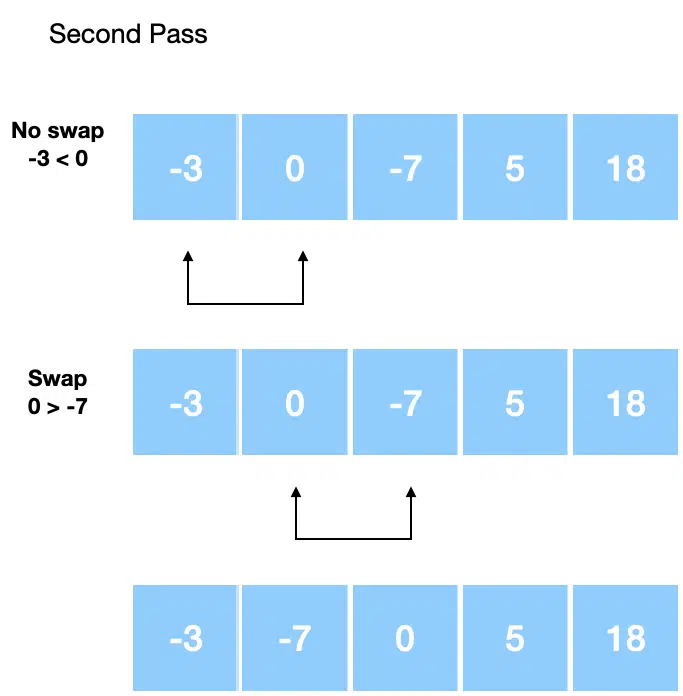
The algorithm only swaps elements if the right element is less than the left element in the array. Finally, we have the third pass:

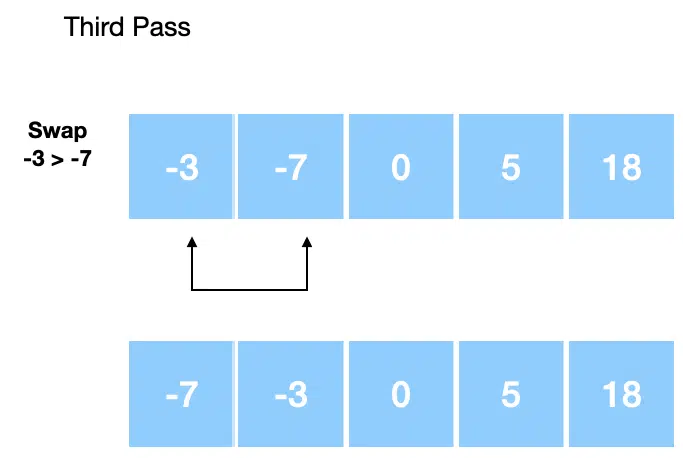
The number of passes over the array depends on the array size and the arrangement of the array elements.

Below, you can see a visualization of how Bubble Sort works. Choose the length of your array in the box next to Array Size (Max 30) then click Generate Random Array to generate the numbers, then click Start Sorting.

Bubble Sort Pseudocode

Let’s look at the pseudo-code describing the bubble sort algorithm

function BubbleSort(arr):
    n = length(arr)

    # Outer loop for each pass
    for i from 0 to n-1:
        swapped = false
        
        # Inner loop for each comparison
        for j from 0 to n-i-2:
            if arr[j] > arr[j+1]:
                swap arr[j] and arr[j+1]
                swapped = true
        
        # If no elements were swapped, break out of the loop
        if swapped is false:
            break

Explanation of the Pseudocode:

1. Outer loop (i): Runs from 0 to n-1, ensuring all elements are sorted after the required passes.
2. Inner loop (j): Compares adjacent elements (arr[j] and arr[j+1]) and swaps them if they are in the wrong order (i.e., if the element on the left is larger than the element on the right).
3. Swapped flag: After each pass, it checks whether any swaps were made. If no swaps were made, the array is already sorted, and the algorithm can terminate early.
4. Termination condition: If no swaps occurred during a pass, the algorithm breaks out of the loop, indicating that the array is already sorted.

Bubble Sort in Python Ascending Order

Let’s look at how to implement the bubble sort algorithm in Python. We will use the algorithm to sort an array of numbers in ascending order.

# Bubble sort algorithm in Python (Ascending Order)
def bubble_sort(arr):
    # Loop for getting each array element
    for i in range(len(arr)):
        # Loop to compare adjacent array elements
        for j in range(0, len(arr) - i - 1):
        # Compare two adjacent elements
            if arr[j] > arr[j + 1]:
                temp = arr[j]
                arr[j] = arr[j+1]
                arr[j+1] = temp
data = [-3, 18, 0, -7, 5]
bubble_sort(data)
print('Array sorted in ascending order using bubble sort: ')
print(data)

Array sorted in ascending order using bubble sort: 
[-7, -3, 0, 5, 18]

Bubble Sort in Python Descending Order

We can also use the bubble sort algorithm to sort by descending order. In comparing the two adjacent elements, instead of swapping if the left element is greater than the right element, we swap if the left element is less than the right one.

# Bubble sort algorithm in Python (Descending Order)
def bubble_sort(arr):
    # Loop for getting each array element
    for i in range(len(arr)):
        # Loop to compare adjacent array elements
        for j in range(0, len(arr) - i - 1):
        # Compare two adjacent elements
        # Changed > to  < to sort in descending order
            if arr[j] < arr[j + 1]:
                temp = arr[j]
                arr[j] = arr[j+1]
                arr[j+1] = temp
data = [-3, 18, 0, -7, 5]
bubble_sort(data)
print('Array sorted in descending order using bubble sort: ')
print(data)

Array sorted in descending order using bubble sort: 
[18, 5, 0, -3, -7]

Optimized Bubble Sort in Python

In the above example, we compare all elements in the array. We can optimize the algorithm only to make comparisons between unsorted elements. Let’s look at the optimized code below:

def bubble_sort(arr):
    for i in range(len(arr)):
        is_swapped = False
        for j in range(0, len(arr) - i - 1):
            if arr[j] > arr[j + 1]:
                temp = arr[j]
                arr[j] = arr[j+1]
                arr[j+1] = temp
                is_swapped = True
        if not is_swapped:
            break
data = [-3, 18, 0, -7, 5]
bubble_sort(data)
print('Array sorted in ascending order using optimized bubble sort: ')
print(data)

We introduce a new variable, is_swapped, which we set to True if we swap the elements after comparison. Otherwise, we put it to False. After a comparison, if we do not swap the elements, we set is_swapped to False. We use an if statement to check the value of is_swapped. If we get False, we break out of the loop, ensuring that we do not compare already sorted elements.

Array sorted in ascending order using optimized bubble sort: 
[-7, -3, 0, 5, 18]

Bubble Sort Timing Comparison

Let’s compare the time it takes to sort the array with and without the optimization.

import time

def bubble_sort(arr):
    # Loop for getting each array element
    for i in range(len(arr)):
        # Loop to compare adjacent array elements
        for j in range(0, len(arr) - i - 1):
        # Compare two adjacent elements
            if arr[j] > arr[j + 1]:
                temp = arr[j]
                arr[j] = arr[j+1]
                arr[j+1] = temp

def bubble_sort_opt(arr):
    for i in range(len(arr)):
        is_swapped = False
        for j in range(0, len(arr) - i - 1):
            if arr[j] > arr[j + 1]:
                temp = arr[j]
                arr[j] = arr[j+1]
                arr[j+1] = temp
                is_swapped = True
        if not is_swapped:
            break

if __name__=='__main__':
    data = [-3, 18, 0, -7, 5]
    t = time.process_time()
    bubble_sort(data)
    elapsed = time.process_time() - t
    data_2 = [-3, 18, 0, -7, 5]
    t2 = time.process_time()
    bubble_sort_opt(data_2)
    elapsed_2 = time.process_time() - t2
    print(f'Sorted array: {data}') 
    print(f'Sorted array: {data_2}')
    print(f'(Time taken for Bubble Sort: {elapsed}')
    print(f'(Time taken for Optimized Bubble Sort: {elapsed_2}')                                                               

In the above code, we use the two bubble sort algorithms on the same unsorted array and time them using the time module. Let’s run the code to see the result:

Sorted array: [-7, -3, 0, 5, 18]
Sorted array: [-7, -3, 0, 5, 18]
(Time taken for Bubble Sort: 1.2999999999999123e-05
(Time taken for Optimized Bubble Sort: 5.999999999999062e-06

The optimized algorithm takes approximately half as long to sort the array. Though the time taken for either is very small, the time difference will be more significant with larger unsorted arrays. Also, if you are using the process recurrently on many arrays, the time saved using the optimized algorithm will quickly accumulate.

Bubble Sort Complexity

Time Complexity

Bubble sort employs two loops: an inner loop and an outer loop. The number of comparisons made is:

(n - 1 ) + (n - 2) + (n - 3) + ... + 1 = n(n-1)/2

Which approximates to n²; therefore, the complexity of the bubble sort algorithm is O(n²).

Bubble Sort Worst Case Time Complexity

• The outer loop runs O(n) times.
• As a result, the worst-case time complexity of bubble sort is O(n × n) = O(n²).
• This is also the average case complexity, meaning that the elements of the array are in jumbled order and are neither ascending nor descending. This complexity occurs because, regardless of the arrangement of elements, the number of comparisons remains the same.

Bubble Sort Best Case Time Complexity

• The outer loop runs O(n) times if the list is already sorted.

Space Complexity

• Space complexity is O(1) because we use an extra variable temp for swapping.
• In the optimized bubble sort algorithm we use two extra variables temp and is_swapped. Therefore the space complexity is O(2).

Summary

Congratulations on reading to the end of this tutorial! We have gone through implementing the bubble sort algorithm in Python and optimising it. This algorithm is suitable for cases where complexity does not matter, and simplicity in code is preferable.

Ready to see sorting algorithms come to life? Visit the Sorting Algorithm Visualizer on GitHub to explore animations and code.

For further reading on the Rust implementation of Bubble Sort, go to the article: How to Do Bubble Sort in Rust.

For reading on Cocktail Sort, a bidirectional variation of Bubble Sort, go to the article: How To Do Cocktail Sort in Python.

For further reading on other sorting algorithms in Python, go to the articles:

• How to do Insertion Sort in Python
• How to do Quick Sort in Python
• How to do Merge Sort in Python
• How to Do Selection Sort in Python
• How to do Counting Sort in Python
• How to Do Radix Sort in Python
• How to Do Bucket Sort in Python
• How to Do Heap Sort in Python
• How to Do Pigeonhole Sort in Python
• How To Do Comb Sort in Python 
• How to Do Shell Sort in Python
• How To Do TimSort in Python

Go to the online courses page on Python to learn more about coding in Python for data science and machine learning.

Have fun and happy researching!