How to Write the Fibonacci Sequence in C++

In mathematics, the Fibonacci sequence is a sequence of numbers where each number is the sum of the two preceding numbers. For example:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 65, ..

The sequence starts with 0 and 1, and we find the following number by summing the two numbers that occur before it.

In the case of the third number in the sequence, the two preceding numbers are 0 and 1, so the third number is (0 + 1) = 1.

In the case of the fourth number in the sequence, the two preceding numbers are 1 and 1, so the fourth number is (1 + 1) = 2.

Each number in the Fibonacci sequence is a Fibonacci number, F(N).

This tutorial will go through how to write the Fibonacci sequence in C++ using both an iterative and recursive method.

---

Iterative Implementation of the Fibonacci Sequence in C++

We can implement the Fibonacci sequence both iteratively and recursively in C++. Let’s go through how to do each with the help of some code snippets.

#include <stdio.h>
#include <iostream>
using namespace std;
int main() {

    int i, n;

    // First terms

    int t1 = 0, t2 = 1;

    // 3rd term
    int nextTerm = t1 + t2;

    // Request number of terms from user
    cout << "Enter the number of terms of series : ";

    cin >> n;

    // Print first two terms
    cout << "Fibonacci Series: " << t1 <<", " << t2 << ", " ;

    // Print 3rd to nth terms
    for (i = 3; i <= n; ++i) {

        printf("%d, ", nextTerm);

        t1 = t2;

        t2 = nextTerm;

        nextTerm = t1 + t2;

    }

    return 0;
}

In the above implementation, the function defines the first two terms as 0 and 1. Then we get the third term by adding the first and second terms. We request the number of terms from the user using std::cin and use a for loop to print each Fibonacci number up to the specified number of terms.

Each iteration determines the next value in the sequence by summing the two previous values then updating the values of t1 and t2.

Let’s run the code to see the result:

Enter the number of terms: 10
Fibonacci Series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 

Recursive Implementation of the Fibonacci Sequence in C++

Recursion is when a function refers to itself to solve a problem. In every function call, the problem becomes smaller until the call reaches a base case, after which it will return the result to each intermediate call until it returns the final result to the first call.

Let’s look at the example of calculating the fifth Fibonacci number, F(5). First, we will need to calculate its preceding numbers to do this calculation. F(4) and F(3). Then to calculate F(4) and F(3), you would need to calculate their preceding numbers and so on. The complete recursive solution for F(5) would look as follows:

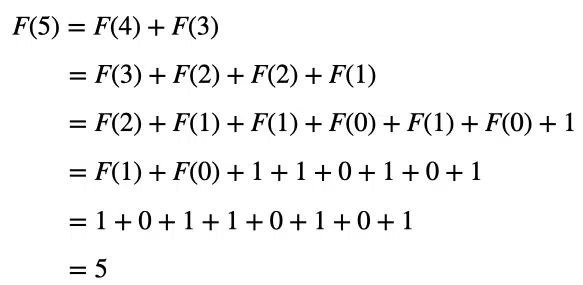
Each time we call the Fibonacci function, the problem breaks up into smaller component problems. When the function eventually reaches the base case of either F(0) or F(1), it will return the result to the caller. Let’s look at how to implement the recursive solution in C++:

#include <iostream>
using namespace std;
int fib(int n) {
   if((n==1)||(n==0)) {
      return(n);
   }else {
      return(fib(n-1)+fib(n-2));
   }
}

In the above function, we use recursion to generate the Fibonacci sequence. The procedure takes the parameter n. If the number is 0 or 1, the function will return the value of n. Otherwise, it will recursively call the fib_recursive function with n-1 and n-2.

Next, we get the number of terms from the user using std::cin. We will use this number in a while loop to iteratively call the recursive Fibonacci function for each number between 0 and the input number. The result will be the Fibonacci sequence. Let’s look at the main function:

int main() {

   int n , i=0;

   cout << "Enter the number of terms of series : ";

   cin >> n;

   cout << "\nFibonnaci Series : ";

   while(i < n) {

      cout << " " << fib(i);

      i++;

   }

   return 0;

}

Let’s run the code to get the result:

Enter the number of terms of series : 10

Fibonnaci Series :  0 1 1 2 3 5 8 13 21 34

Summary

Congratulations on reading to the end of this tutorial! You have gone through implementing the Fibonacci sequence in C++ both iteratively and recursively. The Fibonacci Sequence and Fibonacci numbers are ubiquitous in nature and underpin fascinating mathematical expressions. Learning how to implement the Fibonacci sequence is particularly helpful for understanding how recursion works in C++.

To learn how to implement the Fibonacci sequence in Python, go to the article: How to Write the Fibonacci Sequence in Python.

Have fun and happy researching!