Table of Contents
Introduction to One-Proportion Z-Tests
The one-proportion Z-test is a vital statistical tool for assessing whether a sample proportion significantly deviates from a hypothesized population proportion. It’s commonly applied in scenarios like evaluating customer satisfaction rates, election polls, or clinical trials.
By comparing observed data to theoretical expectations, this test helps statisticians determine if deviations are meaningful or simply due to chance. In this guide, we’ll explore how to calculate and interpret the test using Python, ensuring your analysis is both rigorous and insightful.
Calculating the One-Proportion Z-Test in Python
The formula for the Z-score in a one-proportion test is:
\[ Z = \frac{\hat{p} – p_0}{\sqrt{\frac{p_0 (1 – p_0)}{n}}} \]Where:
- \( \hat{p} \): Observed proportion
- \( p_0 \): Hypothesized proportion
- \( n \): Sample size
Here’s the Python code for calculating the Z-score and p-value:
import math
from scipy.stats import norm
# Inputs
observed_successes = 45
sample_size = 100
hypothesized_proportion = 0.50
# Calculations
observed_proportion = observed_successes / sample_size
z_score = (observed_proportion - hypothesized_proportion) / math.sqrt(hypothesized_proportion * (1 - hypothesized_proportion) / sample_size)
p_value = 2 * (1 - norm.cdf(abs(z_score)))
print("Z-score:", z_score)
print("P-value:", p_value)
P-value: 0.31731050786291415
The p-value of 0.317 is greater than the standard significance level of 0.05, so we fail to reject the null hypothesis. This suggests no significant evidence that the observed proportion (\( \hat{p} = 0.45 \)) differs from the hypothesized proportion (\( p_0 = 0.50 \)).
Calculating the Power of the Test
The power of a test is the probability of correctly rejecting the null hypothesis when it is false. Power depends on the significance level (\( \alpha \)), the sample size (\( n \)), and the effect size (\( d \)).
Here’s the Python code for calculating the power of the test:
Calculating the Power
# True proportion for power calculation
true_proportion = 0.45 # Assumed true value for power analysis
alpha = 0.05 # Significance level
# Critical Z-value
z_critical = norm.ppf(1 - alpha / 2)
# Standard error and effect size
standard_error = math.sqrt(hypothesized_proportion * (1 - hypothesized_proportion) / sample_size)
effect_size = (true_proportion - hypothesized_proportion) / standard_error
# Power calculation
power = norm.cdf(-z_critical + effect_size) + (1 - norm.cdf(z_critical + effect_size))
print("Power of the test:", power)
Calculating the Effect Size
Effect size provides a measure of the practical significance of the difference between the observed and hypothesized proportions, moving beyond the binary decision of statistical significance. While a p-value helps determine if a result is statistically significant, effect size quantifies the magnitude of the difference, making it an essential component of any hypothesis test.
Cohen’s \( h \): A Metric for Proportions
Cohen’s \( h \) is a widely used effect size metric for comparing proportions. It captures the standardized difference between the observed sample proportion (\( \hat{p} \)) and the hypothesized population proportion (\( p_0 \)):
\[ h = 2 \times \arcsin(\sqrt{\hat{p}}) – 2 \times \arcsin(\sqrt{p_0}) \]Here’s how to calculate Cohen’s \( h \) in Python:
# Effect size calculation using Cohen's h
effect_size = 2 * (math.asin(math.sqrt(observed_proportion)) - math.asin(math.sqrt(hypothesized_proportion)))
print("Effect size (Cohen's h):", effect_size)
Applying it to our example we get:
In our example, the observed proportion (\( \hat{p} = 0.45 \)) showed no significant difference from the hypothesized proportion (\( p_0 = 0.50 \)), with a p-value of 0.317. However, the test’s power was only 17%, indicating the sample size of 100 is insufficient for reliable conclusions. The small effect size (\( h = -0.10 \)) further suggests the difference is minimal in practical terms. Let’s see how increasing the sample size improves power.
Power vs. Sample Size Plot
This plot demonstrates how the power of a one-proportion Z-test increases with the sample size. As the sample size grows, the test becomes more likely to detect a true difference when it exists, emphasizing the importance of a sufficiently large sample.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters
p0 = 0.50 # Hypothesized proportion (the value we're testing against)
true_p = 0.45 # Assumed true proportion (the real population proportion)
alpha = 0.05 # Significance level (threshold for rejecting the null hypothesis)
sample_sizes = np.arange(10, 1000, 10) # Range of sample sizes to calculate power
powers = [] # Empty list to store power values for each sample size
# Calculate power for each sample size
for n in sample_sizes:
# Calculate the standard error for the current sample size
se = np.sqrt(p0 * (1 - p0) / n)
# Calculate the critical Z-value for a two-tailed test
z_critical = norm.ppf(1 - alpha / 2)
# Calculate the effect size (difference between true proportion and hypothesized proportion in SE units)
effect_size = (true_p - p0) / se
# Calculate the power of the test
# Power is the sum of probabilities of detecting the effect in both tails
power = norm.cdf(-z_critical + effect_size) + (1 - norm.cdf(z_critical + effect_size))
# Append the calculated power to the list
powers.append(power)
# Plot the results
plt.figure(figsize=(8, 5)) # Set the figure size
plt.plot(sample_sizes, powers, label="Power", color="black") # Plot power vs. sample size
plt.axhline(0.8, color="red", linestyle="--", label="80% Power Threshold") # Add 80% power threshold
plt.title("Power vs. Sample Size") # Title of the plot
plt.xlabel("Sample Size") # Label for the x-axis
plt.ylabel("Power") # Label for the y-axis
plt.legend() # Show the legend
plt.show() # Display the plot
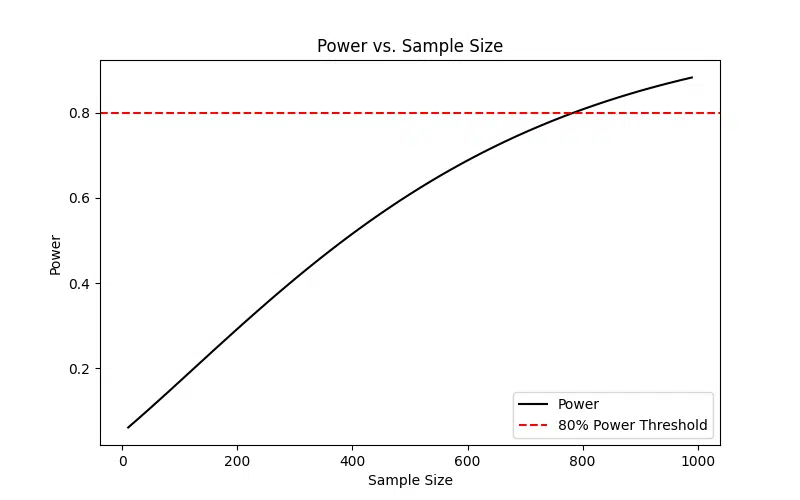
The graph above illustrates how the statistical power of a one-proportion Z-test increases with the sample size. Power represents the probability of correctly rejecting the null hypothesis when it is false. As the sample size grows, the standard error decreases, making it easier to detect smaller differences between the observed and hypothesized proportions.
The red dashed line at 80% represents the commonly accepted threshold for adequate power in hypothesis testing. Below this threshold, the test has a higher likelihood of committing a Type II error (failing to reject a false null hypothesis). This highlights the importance of selecting a sufficiently large sample size during the study design phase to ensure reliable and meaningful results.
For small sample sizes, the power remains low, even if there is a true effect, making it difficult to detect significant differences. By increasing the sample size, we improve the precision of the test, reducing uncertainty and increasing confidence in the findings.
Assumptions and Limitations
❗The one-proportion Z-test is a powerful statistical tool, but its accuracy depends on several key assumptions. Failing to meet these assumptions can lead to misleading results. Below are the detailed conditions that must be satisfied:
Assumptions
-
Sufficiently large sample size:
The sample size should generally be larger than 30 to ensure the normal approximation of the binomial distribution holds true. This is crucial because the Z-test relies on the assumption that the sampling distribution of the proportion is approximately normal. For smaller sample sizes, consider using a binomial test instead.
-
Binary outcomes:
The test is applicable when data consists of two possible outcomes, such as success/failure, yes/no, or satisfied/not satisfied. This ensures that the underlying binomial distribution is valid for calculating proportions.
-
Independent observations:
Each observation in the sample must be independent of the others. For example, the satisfaction of one customer should not influence the satisfaction of another. Violating this assumption, such as in clustered or dependent data, can bias the results and invalidate the test.
Limitations
-
Not suitable for small sample sizes:
When the sample size is small, the normal approximation may not hold, making the Z-test unreliable. Specifically, the Z-test may be inappropriate when either $n * p_{0} < 5$ or $n *(1 - p_0) < 5$, where $n$ is the sample size and $p_{0}$ is the hypothesized proportion. In such cases, a binomial test, which does not rely on the normal approximation, is preferred for more accurate results.
-
Sensitive to extreme proportions:
The test becomes less reliable when the hypothesized proportion (\( p_0 \)) is close to 0 or 1. In such cases, the normal approximation may break down, leading to inaccurate results. This is because the binomial distribution becomes highly skewed for extreme probabilities.
-
Reliance on approximation:
The one-proportion Z-test assumes that the standard error is based on the hypothesized proportion (\( p_0 \)). If the true proportion deviates significantly from \( p_0 \), the results may be misleading. In these cases, alternative methods, such as bootstrapping, may provide more robust insights.
-
Low power with small effect sizes:
When the effect size (difference between observed and hypothesized proportions) is small, the test may have insufficient power to detect a meaningful difference, especially with moderate sample sizes. This emphasizes the importance of power analysis during study design.
Conclusion
The one-proportion Z-test is a useful tool for determining whether an observed sample proportion differs significantly from a hypothesized population proportion. By calculating the Z-score and interpreting the p-value, we can assess whether the observed proportion is likely due to random chance or represents a significant deviation from the hypothesized value.
In addition to the Z-test, evaluating the power of the test and the effect size provides a more comprehensive understanding of the results. The power helps quantify the likelihood of detecting a true effect, offering critical insights into the reliability of the test, particularly when designing studies or interpreting non-significant results. Effect size, such as Cohen’s \( h \), highlights the practical significance of the observed difference, moving beyond statistical significance to assess the magnitude of the effect.
Try the One-Proportion Z-Test Calculator
💡 For an easy way to calculate the one-proportion Z-test and determine the p-value, you can check out our One-Proportion Z-Test Calculator on the Research Scientist Pod.
Have fun and happy researching!
Suf is a senior advisor in data science with deep expertise in Natural Language Processing, Complex Networks, and Anomaly Detection. Formerly a postdoctoral research fellow, he applied advanced physics techniques to tackle real-world, data-heavy industry challenges. Before that, he was a particle physicist at the ATLAS Experiment of the Large Hadron Collider. Now, he’s focused on bringing more fun and curiosity to the world of science and research online.

