Table of Contents
Introduction
Quadratic regression is a powerful technique used to model relationships between variables that follow a curved trajectory. Unlike linear regression, which fits a straight line to data, quadratic regression captures more complex patterns by fitting a parabolic curve. This makes it especially useful in scenarios where linear models fall short.
This guide explores the implementation of quadratic regression in Python, covering the mathematical foundations, step-by-step code examples, and practical applications. Using popular libraries such as NumPy, Scikit-learn, and Statsmodels, the guide offers a comprehensive approach to understanding and applying this technique.
By understanding quadratic regression, you can analyze datasets with curved relationships more effectively, unlocking insights that would be missed with simpler models. Let’s begin by delving into the foundational concepts that underpin this method.
Mathematical Foundations
Quadratic regression models the relationship between an independent variable (\(x\)) and a dependent variable (\(y\)) using a second-degree polynomial equation. The model can be written as:
\[ y = \beta_0 + \beta_1x + \beta_2x^2 + \epsilon \]
Each term in this equation has a specific meaning:
- \( y \): The dependent variable, or the outcome we aim to predict.
- \( x \): The independent variable, or the input used to make predictions.
- \( \beta_0 \): The intercept, representing the value of \(y\) when \(x = 0\).
- \( \beta_1 \): The linear coefficient, quantifying the linear relationship between \(x\) and \(y\).
- \( \beta_2 \): The quadratic coefficient, capturing the curvature of the relationship.
- \( \epsilon \): The error term, accounting for variability in \(y\) not explained by the model.
The quadratic term (\( \beta_2x^2 \)) is what distinguishes this model from simple linear regression. It allows the curve to bend, making quadratic regression ideal for datasets where the relationship between variables is non-linear, such as U-shaped or inverted U-shaped patterns.
For example, in economics, quadratic regression can model diminishing returns, where the benefit of adding more input decreases over time. In physics, it can represent projectile motion, where the height of an object depends on time in a parabolic trajectory.
With a solid understanding of the mathematical structure, we’re ready to move on to implementing quadratic regression in Python.
Using NumPy
NumPy simplifies polynomial regression by providing functions to calculate polynomial coefficients and evaluate polynomial values. Here’s a step-by-step implementation of quadratic regression using NumPy:
import numpy as np
import matplotlib.pyplot as plt
# Generate sample data
np.random.seed(0)
X = np.linspace(-5, 5, 100)
y = 2 * X**2 - 4 * X + 1 + np.random.normal(0, 3, 100)
# Fit quadratic regression
coefficients = np.polyfit(X, y, 2)
y_pred = np.polyval(coefficients, X)
print(f"Quadratic coefficient (β₂): {coefficients[0]:.4f}")
print(f"Linear coefficient (β₁): {coefficients[1]:.4f}")
print(f"Intercept (β₀): {coefficients[2]:.4f}")
# Plot results
plt.scatter(X, y, color='blue', alpha=0.5, label='Data')
plt.plot(X, y_pred, color='red', label='Quadratic Fit')
plt.xlabel('X (Independent Variable)')
plt.ylabel('Y (Dependent Variable)')
plt.legend()
plt.show()Explanation:
- Data Generation: We create a dataset with a known quadratic relationship and add random noise using NumPy’s random module to simulate real-world data.
- Polynomial Fitting: The
np.polyfitfunction fits a polynomial of degree 2 (quadratic) to the data and returns the coefficients \( \beta_2, \beta_1, \beta_0 \). - Prediction: Using
np.polyval, we evaluate the polynomial at each \( x \) value to generate predictions (\( y_{\text{pred}} \)). - Visualization: We use Matplotlib to visualize the data points and the fitted quadratic curve for better interpretation of the results.
Linear coefficient (β₁): -4.0892
Intercept (β₀): -0.1417
Visualizing Quadratic Regression with Matplotlib
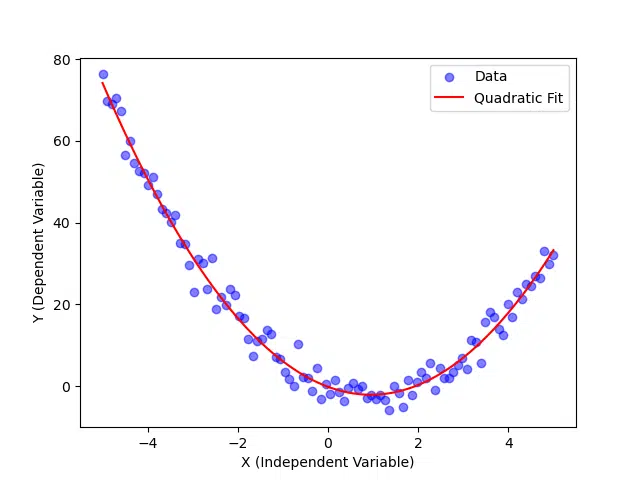
The visualization makes it easy to identify how well the quadratic curve fits the data. If there are large deviations between the curve and the data points, it could indicate issues such as outliers or an incorrect model assumption.
Visualizing Quadratic Regression with Seaborn
Seaborn offers multiple ways to visualize regression, including the versatile lmplot. Unlike regplot, lmplot provides more flexibility for visualizing grouped data and adding facets to plots. With its ability to display confidence intervals, lmplot is an excellent choice for visualizing both the fit and the uncertainty around the regression curve.
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# Prepare data
np.random.seed(0)
X = np.linspace(-5, 5, 100)
y = 2 * X**2 - 4 * X + 1 + np.random.normal(0, 3, 100)
data = pd.DataFrame({'X': X, 'y': y})
# Create an lmplot for quadratic regression
plot = sns.lmplot(
data=data,
x="X",
y="y",
order=2,
height=6,
aspect=1.5,
scatter_kws={"alpha": 0.5, "label": "Data Points"},
line_kws={"color": "red", "label": "Regression Line"}
)
# Customize the plot
plot.set_axis_labels("X (Independent Variable)", "Y (Dependent Variable)")
plt.legend(loc="upper right", title="Legend") # Add a legend
plt.title("Quadratic Regression Visualization with Seaborn")
plt.show()
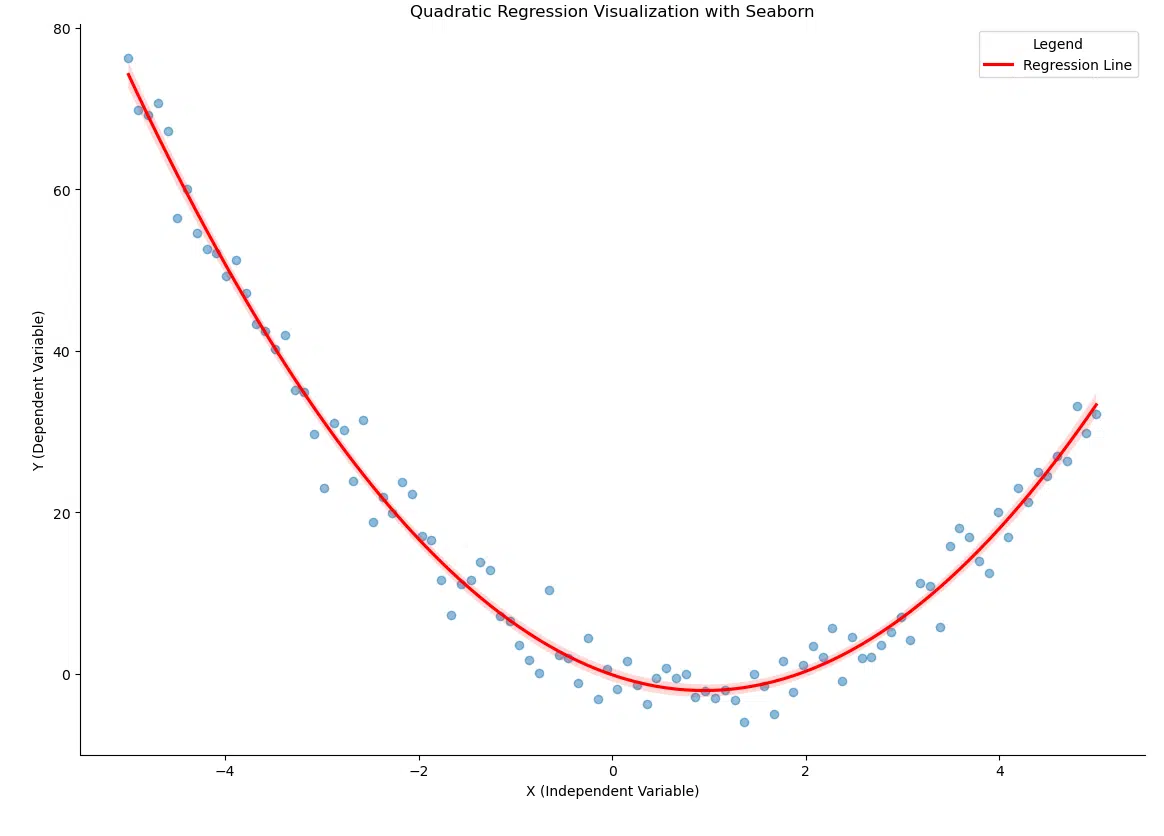
lmplot visualization of quadratic regression. The red curve represents the quadratic fit, and the shaded area shows the confidence interval.
The visualization highlights the quadratic relationship between the variables, with the confidence interval providing additional insight into the uncertainty of the model. Compared to regplot, lmplot offers more flexibility, such as supporting faceted plots for grouped or categorized data.
The confidence interval (shaded area) is particularly useful for identifying areas of uncertainty in the regression model. For instance, as the dataset becomes sparse toward the edges, the confidence interval widens, indicating less certainty in the predictions.
NumPy Model Evaluation
Evaluating a regression model involves assessing how well it predicts the dependent variable. In this section, we’ll use two widely recognized metrics: the R² score and the Root Mean Squared Error (RMSE). These metrics provide complementary insights into the model’s performance.
from sklearn.metrics import r2_score, mean_squared_error
import numpy as np
# Calculate metrics
r2 = r2_score(y, y_pred)
rmse = np.sqrt(mean_squared_error(y, y_pred))
print(f"R² Score: {r2:.4f}")
print(f"RMSE: {rmse:.4f}")Explanation:
- R² Score: This metric quantifies the proportion of the variance in the dependent variable (\( y \)) that is explained by the independent variable (\( x \)). An R² score of 1 indicates a perfect fit, while a score closer to 0 suggests the model has little explanatory power.
- Root Mean Squared Error (RMSE): RMSE measures the average magnitude of the prediction errors, providing a sense of how far the model’s predictions are from the actual values. Lower RMSE values indicate better performance.
- Usage in Code: The
r2_scorefunction calculates the R² score, whilemean_squared_errorcomputes the mean squared error, which is then square-rooted to obtain the RMSE.
RMSE: 2.7711
These metrics highlight the strengths and limitations of the quadratic regression model. In this example, an R² score of 0.9816 indicates that the model explains 98.16% of the variance in the data, while an RMSE of 2.7711 suggests relatively small prediction errors.
While these metrics provide valuable insights, it’s also essential to consider the specific context of your data and application. In the next section, we’ll explore a more structured implementation using Scikit-learn.
Using Scikit-learn
Scikit-learn is a powerful library for machine learning that provides built-in tools for polynomial regression. Using its PolynomialFeatures class and LinearRegression model, we can implement quadratic regression in a structured way, making it easier to scale and evaluate.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
# Create and fit the model
model = make_pipeline(
PolynomialFeatures(degree=2),
LinearRegression()
)
model.fit(X.reshape(-1, 1), y)
# Get predictions
y_pred = model.predict(X.reshape(-1, 1))
# Print coefficients
coefficients = model.named_steps['linearregression'].coef_
intercept = model.named_steps['linearregression'].intercept_
print(f"Coefficients: {coefficients}")
print(f"Intercept: {intercept:.4f}")
print(f"R² Score: {model.score(X.reshape(-1, 1), y):.4f}")Explanation:
- Pipeline Creation: The
make_pipelinefunction combines multiple processing steps into a single model pipeline. Here, we first transform the input data to include polynomial terms (degree 2) usingPolynomialFeatures, and then apply linear regression to the transformed data. - Data Transformation: The
PolynomialFeaturesstep automatically generates additional features, such as \( x^2 \), making the model capable of fitting a quadratic curve. - Model Fitting: The
fitmethod trains the pipeline by finding the best coefficients (\( \beta_2, \beta_1, \beta_0 \)) to minimize the prediction error. - Model Predictions: The
predictmethod generates predictions for the input data using the trained model. - Coefficient Extraction: We access the linear regression step in the pipeline to extract the coefficients and intercept, which provide insights into the model’s parameters.
- Performance Evaluation: The R² score, calculated using
model.score, quantifies how well the model explains the variability in the data.
Intercept: -0.1417
R² Score: 0.9816
Analysis of Results:
- Coefficients: The quadratic coefficient (\( \beta_2 = 2.1554 \)) and linear coefficient (\( \beta_1 = -4.0892 \)) closely match the results obtained with the NumPy implementation. The intercept (\( \beta_0 = -0.1417 \)) also aligns well.
- R² Score: The R² score of 0.9816 indicates that this model explains 98.16% of the variance in the data, suggesting an excellent fit.
Comparison to NumPy Implementation:
- Similar Results: Both implementations yield nearly identical coefficients, confirming the consistency and accuracy of the quadratic regression model.
- Additional Insights: Scikit-learn provides a structured approach that is more scalable and integrates seamlessly into machine learning workflows, whereas NumPy is lightweight and suitable for quick calculations.
- Performance Evaluation: The R² score is slightly higher in the Scikit-learn implementation, likely due to subtle differences in data handling and numerical precision.
Scikit-learn’s structured approach is particularly useful for scaling up to larger datasets or integrating the model into broader machine learning pipelines. In the next section, we’ll explore another implementation using Statsmodels, which offers detailed statistical summaries of the model.
Using Statsmodels
Statsmodels is a library designed for statistical modeling and testing, providing detailed outputs and diagnostics. It is particularly useful when you need a deeper understanding of your model’s performance and the statistical significance of its parameters. Here’s how to implement quadratic regression using Statsmodels:
import statsmodels.api as sm
# Prepare data
X_quad = sm.add_constant(np.column_stack((X, X**2)))
# Fit model
model = sm.OLS(y, X_quad).fit()
# Print summary
print(model.summary())Explanation:
- Data Preparation: Statsmodels requires the independent variables to be in a matrix format. We use
np.column_stackto combine \(x\) and \(x^2\) into a single matrix and add a constant term for the intercept usingsm.add_constant. - Model Fitting: The
OLS(Ordinary Least Squares) method fits the quadratic regression model by minimizing the squared difference between the observed and predicted values. - Statistical Summary: The
summarymethod provides a detailed report, including parameter estimates, standard errors, t-statistics, and p-values. These metrics help assess the significance of each term in the model.
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.982
Model: OLS Adj. R-squared: 0.981
Method: Least Squares F-statistic: 2594.
Date: Fri, 03 Jan 2025 Prob (F-statistic): 6.17e-85
Time: 20:22:31 Log-Likelihood: -243.82
No. Observations: 100 AIC: 493.6
Df Residuals: 97 BIC: 501.5
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -0.1417 0.422 -0.336 0.738 -0.979 0.696
x1 -4.0892 0.096 -42.377 0.000 -4.281 -3.898
x2 2.1554 0.037 58.244 0.000 2.082 2.229
==============================================================================
Omnibus: 0.116 Durbin-Watson: 2.174
Prob(Omnibus): 0.944 Jarque-Bera (JB): 0.001
Skew: -0.005 Prob(JB): 1.00
Kurtosis: 3.008 Cond. No. 17.2
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Analysis of Results:
- R-squared: The R-squared value of 0.982 indicates that the model explains 98.2% of the variance in the dependent variable. This aligns closely with the Scikit-learn implementation, confirming a strong fit to the data.
- Coefficients: The coefficients for the quadratic term (\( \beta_2 = 2.1554 \)), linear term (\( \beta_1 = -4.0892 \)), and intercept (\( \beta_0 = -0.1417 \)) are consistent with the results from NumPy and Scikit-learn, highlighting the reliability of the model across implementations.
- Statistical Significance: The p-values for the coefficients (\( <0.05 \)) confirm their statistical significance, indicating that each term contributes meaningfully to the model.
- Model Diagnostics: Metrics like the AIC (493.6) and BIC (501.5) provide a measure of model quality, useful for comparing with alternative models. The Durbin-Watson statistic (2.174) suggests no significant autocorrelation in the residuals. Autocorrelation occurs when the residuals (errors) of the model are correlated with each other rather than being random. A lack of autocorrelation, as indicated by the Durbin-Watson value near 2, means the residuals are independent, which is a key assumption of linear regression.
- Residual Analysis: The Omnibus and Jarque-Bera tests indicate that the residuals are normally distributed, validating the assumptions of the quadratic regression model fitted using ordinary least squares (OLS).
Comparison to NumPy and Scikit-learn Implementations:
- Depth of Analysis: Statsmodels provides more detailed statistical insights, including standard errors, t-statistics, and diagnostic tests, which are not available in NumPy or Scikit-learn.
- Model Coefficients: All three implementations produce consistent coefficients and intercepts, confirming the accuracy and reliability of the quadratic regression model.
- Performance Metrics: The R-squared value in Statsmodels is nearly identical to that in Scikit-learn (0.982 vs. 0.9816), indicating a similarly strong fit. NumPy does not directly provide this metric.
- Ease of Use: While NumPy and Scikit-learn are more streamlined, Statsmodels is ideal for in-depth analysis, particularly when understanding statistical significance and residual behavior is critical.
Statsmodels not only provides a reliable regression model but also equips you with tools to perform detailed statistical analysis. In the next section, we’ll visualize the results of our quadratic regression to better interpret the model.
Model Diagnostics Using Statsmodels
To ensure the reliability and robustness of a regression model, it’s essential to validate the underlying assumptions. This section introduces key diagnostic tests to evaluate residuals, detect heteroscedasticity, and assess multicollinearity in the context of quadratic regression.
import numpy as np
from scipy.stats import shapiro
from statsmodels.stats.diagnostic import het_breuschpagan
from statsmodels.stats.outliers_influence import variance_inflation_factor
import statsmodels.api as sm
# Assume 'model' is a fitted statsmodels OLS model
residuals = model.resid
# Test for normality of residuals (Shapiro-Wilk Test)
shapiro_test_stat, shapiro_p_value = shapiro(residuals)
print(f"Shapiro-Wilk Test Statistic: {shapiro_test_stat:.4f}, p-value: {shapiro_p_value:.4f}")
# Test for heteroscedasticity (Breusch-Pagan Test)
exog = model.model.exog
bp_test_stat, bp_p_value, _, _ = het_breuschpagan(residuals, exog)
print(f"Breusch-Pagan Test Statistic: {bp_test_stat:.4f}, p-value: {bp_p_value:.4f}")
# Calculate Variance Inflation Factor (VIF)
vif_data = [variance_inflation_factor(exog, i) for i in range(exog.shape[1])]
print("VIF Values:", vif_data)Explanation:
-
Normality Test: The
shapirofunction performs the Shapiro-Wilk test, which checks if the residuals (the differences between actual and predicted values) follow a bell-shaped curve, called a normal distribution. Residuals should ideally be normally distributed for the regression model to make accurate predictions. A p-value greater than 0.05 means we cannot reject the idea that the residuals are normal, which is a good outcome.
Think of it like checking if your prediction errors are evenly spread out without any unusual patterns. -
Heteroscedasticity Test: The Breusch-Pagan test evaluates whether the spread of the residuals (their variance) stays consistent across all predicted values. If the variance changes (e.g., residuals get larger as predictions increase), this is called heteroscedasticity and can affect the accuracy of the model. A p-value greater than 0.05 indicates that the residual variance is consistent (homoscedasticity), which is what we want.
Imagine if your model’s errors were small for some data but huge for others—that’s what we’re testing to avoid. -
Multicollinearity Test: Variance Inflation Factor (VIF) measures whether the predictors (independent variables) in the model are too closely related to each other. High multicollinearity can make it difficult for the model to determine the individual effect of each predictor. A VIF above 10 means there’s a problem, but values closer to 1 suggest no significant overlap.
Think of VIF like checking if two predictors are saying the same thing—if they are, it could confuse the model.
Shapiro-Wilk Test Statistic: 0.9958, p-value: 0.9903
Breusch-Pagan Test Statistic: 1.6000, p-value: 0.4493
VIF Values: [2.2504, 1.0000, 1.0000]
Analysis of Results:
- Shapiro-Wilk Test: The test statistic of 0.9958 and a p-value of 0.9903 suggest that the residuals are normally distributed, meeting a key assumption of regression models.
- Breusch-Pagan Test: With a test statistic of 1.6000 and a p-value of 0.4493, there is no evidence of heteroscedasticity, indicating that the variance of the residuals is constant.
- VIF Values: The VIF values for all predictors are below 2.5, well within the acceptable range (less than 10), suggesting no significant multicollinearity in the model.
These diagnostics confirm that the quadratic regression model satisfies the assumptions of normality, homoscedasticity, and low multicollinearity, ensuring reliable and robust results.
Best Practices
Ensuring the reliability and robustness of a regression model requires more than just fitting the data. Quadratic regression, like any modeling technique, is susceptible to pitfalls and overfitting. By following best practices, you can enhance the accuracy and interpretability of your model.
Tips for Effective Quadratic Regression:
- Visualize Your Data: Before applying quadratic regression, plot the data to verify that a quadratic relationship exists. Look for patterns that justify the use of a parabolic model.
- Handle Outliers Carefully: Outliers can disproportionately influence the regression model, leading to skewed coefficients. Consider removing or mitigating their effects with robust statistical methods.
- Feature Scaling: Standardize or normalize your independent variable(s) when combining features of vastly different scales. This ensures numerical stability, particularly in larger datasets.
- Cross-Validation: Use techniques like k-fold cross-validation to evaluate the model on unseen data. This helps identify potential overfitting and ensures the model generalizes well.
- Inspect Residuals: Analyze residuals (differences between actual and predicted values) to check for patterns. A good regression model should have residuals that are randomly distributed around zero.
Common Pitfalls to Avoid:
- Assuming a Quadratic Relationship Without Validation: Not all curved relationships are quadratic. Higher-degree polynomial or non-linear models may sometimes be more appropriate.
- Overfitting: Adding more polynomial terms can lead to a model that fits the training data too closely but performs poorly on new data. Keep the model as simple as possible while maintaining accuracy.
- Extrapolation Risks: Avoid making predictions far outside the range of your data. Quadratic models, in particular, can produce extreme predictions in such cases.
- Ignoring Domain Knowledge: Consider the context of your problem. Quadratic regression might not align with the underlying physical or logical constraints of the data.
By adhering to these practices, you can build regression models that are both accurate and reliable. In the next section, we’ll conclude with a summary of key insights and recommendations for using quadratic regression effectively.
Conclusion
Quadratic regression is a versatile modeling technique that bridges the gap between linear regression and more complex non-linear methods. By fitting a parabolic curve, it captures relationships in data that cannot be accurately modeled with a straight line, making it an essential tool in the data scientist’s arsenal.
In this guide, we explored the mathematical foundations of quadratic regression and implemented it using three popular Python libraries: NumPy, Scikit-learn, and Statsmodels. Each approach highlighted unique strengths:
- NumPy: Lightweight and efficient for quick polynomial fitting and prediction.
- Scikit-learn: Structured and scalable, suitable for integrating into larger machine learning pipelines.
- Statsmodels: Detailed statistical analysis with comprehensive model diagnostics.
Additionally, we discussed visualization techniques to interpret the model and evaluated its performance using R² and RMSE. These tools and metrics ensure that the model not only fits the data well but also generalizes effectively.
Key Takeaways:
- Use quadratic regression when a curved relationship is evident in the data.
- Visualize your data and residuals to verify assumptions and ensure the model’s reliability.
- Evaluate the model using appropriate metrics like R² and RMSE, and avoid overfitting by keeping the model as simple as possible.
- Choose the implementation method that best suits your needs, balancing efficiency, scalability, and diagnostic requirements.
By following these principles and best practices, you can confidently apply quadratic regression to uncover insights in your data. Whether you’re analyzing trends in economics, modeling physical phenomena, or exploring data in other fields, this method provides a powerful way to capture curved relationships.
We hope this guide serves as a valuable resource for your projects. If you have any questions or additional topics you’d like us to cover, feel free to reach out or explore the further reading section below.
Further Reading
Expand your knowledge with these additional resources on Python programming and regression analysis.
-
Quadratic Regression in R
An in-depth guide to performing quadratic regression in R using Base R, ggplot2, and diagnostic tools, with step-by-step explanations.
-
Quadratic Regression Calculator
Interactive tool to perform quadratic regression analysis with step-by-step guidance and visualization. Ideal for exploring relationships in your data efficiently.
-
Scikit-learn Polynomial Features
Official documentation on implementing polynomial regression in scikit-learn, with detailed examples and best practices.
-
NumPy Polynomial Functions
Comprehensive guide to working with polynomials in NumPy, including fitting and evaluation functions.
-
Statsmodels Regression Models
In-depth documentation on various regression techniques in statsmodels, including diagnostic tools and statistical tests.
-
Matplotlib Gallery
Examples and tutorials for creating publication-quality visualizations of your regression analysis.
-
Polynomial Regression Theory
Theoretical background on polynomial regression, including mathematical foundations and applications.
-
Pandas User Guide
Learn how to effectively prepare and manipulate data for regression analysis using Pandas.
-
SciPy Statistics
Statistical functions and tests useful for regression analysis and model validation.
-
Seaborn Regression Plots
Tutorial on creating informative regression visualizations using Seaborn.
-
Regression Diagnostics
Learn about methods for assessing regression model assumptions and identifying potential issues.
Attribution and Citation
If you found this guide and tools helpful, feel free to link back to this page or cite it in your work!
Suf is a senior advisor in data science with deep expertise in Natural Language Processing, Complex Networks, and Anomaly Detection. Formerly a postdoctoral research fellow, he applied advanced physics techniques to tackle real-world, data-heavy industry challenges. Before that, he was a particle physicist at the ATLAS Experiment of the Large Hadron Collider. Now, he’s focused on bringing more fun and curiosity to the world of science and research online.

