Introduction
Quick Sort is a highly efficient sorting algorithm developed by Tony Hoare in 1959. It employs a divide-and-conquer strategy to sort elements in an array or list. Quick Sort is renowned for its average-case time complexity of O(n log n), making it suitable for large datasets. Its in-place sorting capability (requiring only a small, constant amount of additional memory space) further enhances its practicality.
However, in the worst case, Quick Sort’s performance can degrade to O(n²), typically when the pivot selection is poor (e.g., when the array is already sorted). Various optimizations, such as choosing a better pivot, can mitigate this risk.
In this guide, we’ll explore how to implement Quick Sort in C++, understand its inner workings through pseudocode, and assess its performance through testing.
Understanding the Quick Sort Algorithm
Quick Sort operates based on the following steps:
- Choose a Pivot: Select an element from the array as the pivot. The choice of pivot can affect the algorithm’s performance.
- Partitioning: Rearrange the array so that all elements less than the pivot are on its left, and all elements greater than the pivot are on its right.
- Recursion: Recursively apply the above steps to the sub-arrays on the left and right of the pivot.
Below, you can see a visualization of how Quick Sort works. Choose the length of your array in the box next to Array Size (Max 30) then click Generate Random Array to generate the numbers, then click Start Sorting.

Key Concepts
- In-Place Sorting: Quick Sort sorts the array without additional storage, making it memory-efficient.
- Recursion: Quick Sort relies on recursive calls to sort sub-arrays, which simplifies the implementation but can lead to stack overflow for very large arrays.
- Pivot Selection: The choice of pivot is crucial. Common strategies include selecting the first element, the last element, the middle element, or the median of the first, middle, and last elements (median-of-three).
Time and Space Complexity of Sorting Algorithms
| Algorithm | Best Case | Average Case | Worst Case | Space Complexity |
|---|---|---|---|---|
| Quick Sort | O(n log n) | O(n log n) | O(n²) | O(log n) |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) | O(n) |
| Bubble Sort | O(n) | O(n²) | O(n²) | O(1) |
Pseudocode for Quick Sort
Understanding the pseudocode can provide clarity before diving into code implementation. Here’s a straightforward representation of the Quick Sort algorithm:
function quickSort(array, low, high)
if low < high then
pivotIndex = partition(array, low, high)
quickSort(array, low, pivotIndex - 1)
quickSort(array, pivotIndex + 1, high)
function partition(array, low, high)
pivot = array[high]
i = low - 1
for j from low to high - 1 do
if array[j] < pivot then
i = i + 1
swap array[i] with array[j]
swap array[i + 1] with array[high]
return i + 1
Explanation:
- quickSort Function: This function takes the array and the
lowandhighindices, which define the portion of the array that needs to be sorted. - Base Case: If
lowis not less thanhigh, it means the section of the array is either empty or has only one element, so it’s already sorted. - Partitioning: The partition function reorganizes the array by placing elements smaller than the pivot to the left and larger elements to the right, and then returns the final position of the pivot.
- Recursive Calls: After partitioning, Quick Sort is called recursively on the sub-arrays to the left and right of the pivot until the entire array is sorted.
Diagram Explanation of Quick Sort
To better visualize how Quick Sort works, let’s walk through the sorting process step by step with the array [12, 4, 5, 6, 7, 3, 1, 15].
Step 1:
Original array: [12, 4, 5, 6, 7, 3, 1, 15]
Pivot: 6 (chosen using the median-of-three strategy)
- Partitioning:
- Left:
[4, 5, 3, 1] - Pivot:
[6] - Right:
[12, 7, 15]
- Left:
Step 2:
Recursively sort the left sub-array: [4, 5, 3, 1]
Pivot: 3
Partitioning:
- Left:
[1] - Pivot:
[3] - Right:
[4, 5]
Recursively sort the right sub-array [4, 5]:
- Pivot:
5 - Partitioning:
- Left:
[4] - Pivot:
[5]
- Left:
Step 3:
Recursively sort the right sub-array: [12, 7, 15]
Pivot: 12
Partitioning:
- Left:
[7] - Pivot:
[12] - Right:
[15]
Step 4:
Merge everything:
- Sorted Left:
[1, 3, 4, 5] - Pivot:
[6] - Sorted Right:
[7, 12, 15]
Final sorted array: [1, 3, 4, 5, 6, 7, 12, 15]
Implementing Quick Sort in C++
Let’s translate the pseudocode into a practical C++ implementation. We’ll start with a basic version and then discuss an optimized variant.
Basic Quick Sort Implementation
Here’s a straightforward C++ implementation of Quick Sort based on the above pseudocode:
#include <iostream>
#include <vector>
// Function to swap two elements
void swapElements(int& a, int& b) {
int temp = a;
a = b;
b = temp;
}
// Partition function
int partition(std::vector<int>& arr, int low, int high) {
int pivot = arr[high]; // Choosing the last element as pivot
int i = low - 1; // Index of smaller element
for (int j = low; j <= high - 1; j++) {
// If current element is smaller than pivot
if (arr[j] < pivot) {
i++; // Increment index of smaller element
swapElements(arr[i], arr[j]);
}
}
swapElements(arr[i + 1], arr[high]);
return (i + 1);
}
// Quick Sort function
void quickSort(std::vector<int>& arr, int low, int high) {
if (low < high) {
// pi is partitioning index
int pi = partition(arr, low, high);
// Separately sort elements before and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
// Function to print the array
void printArray(const std::vector<int>& arr) {
for (int num : arr)
std::cout << num << " ";
std::cout << "\n";
}
// Main function to demonstrate Quick Sort
int main() {
std::vector<int> arr = {12, 4, 5, 6, 7, 3, 1, 15};
int n = arr.size();
std::cout << "Original array: ";
printArray(arr);
quickSort(arr, 0, n - 1);
std::cout << "Sorted array: ";
printArray(arr);
return 0;
}
Output:
Original array: 12 4 5 6 7 3 1 15 Sorted array: 1 3 4 5 6 7 12 15
Quick Sort Limitations with Already Sorted Data
Limitations
Quick Sort is a highly efficient algorithm for many types of data; however, when the input data is already sorted (or nearly sorted), it can perform poorly, resulting in a worst-case time complexity of O(n²). This happens because Quick Sort relies on selecting a pivot to partition the array, and when the data is sorted, choosing the first or last element as the pivot leads to highly unbalanced partitions. As a result, the partitioning step repeatedly divides the array in the most inefficient way, creating a significant performance bottleneck.
Example:
For example, in a sorted array [1, 2, 3, 4, 5], if Quick Sort consistently picks the last element as the pivot, each partitioning step only reduces the problem size by one element, leading to a quadratic number of comparisons.
Improvement: Median of Three Pivot Selection
One common improvement to mitigate this issue is to use a median-of-three strategy for pivot selection. Instead of blindly selecting the first or last element, Quick Sort can choose the median of the first, middle, and last elements of the array as the pivot. This strategy helps to ensure that the pivot is more likely to divide the array into balanced partitions, reducing the chance of the worst-case time complexity.
Pseudocode for Median-of-Three:
int medianOfThree(int arr[], int left, int right) {
int mid = left + (right - left) / 2;
if (arr[left] > arr[mid]) swap(arr[left], arr[mid]);
if (arr[left] > arr[right]) swap(arr[left], arr[right]);
if (arr[mid] > arr[right]) swap(arr[mid], arr[right]);
return mid; // Return the index of the median element
}
By using this median-of-three strategy, Quick Sort can avoid unbalanced partitions and perform closer to the optimal O(n log n) time complexity, even when the input array is sorted or nearly sorted.
Other Improvements:
- Randomized Pivot Selection: Another approach is to randomly select a pivot, reducing the likelihood of hitting the worst-case scenario.
- Hybrid Algorithms: For small subarrays, Quick Sort can be combined with algorithms like Insertion Sort, which performs better for smaller data sets.
These improvements significantly reduce the impact of already sorted data and make Quick Sort more robust across different types of input.
Optimized Quick Sort with Median-of-Three Partitioning
To enhance Quick Sort’s performance, especially in avoiding the worst-case scenario, we can implement the median-of-three method for pivot selection. This strategy selects the median of the first, middle, and last elements as the pivot, providing a better partition in many cases.
#include <iostream>
#include <vector>
// Function to swap two elements
void swapElements(int& a, int& b) {
int temp = a;
a = b;
b = temp;
}
// Function to find the median of three elements
int medianOfThree(std::vector<int>& arr, int low, int high) {
int mid = low + (high - low) / 2;
if (arr[low] > arr[mid])
swapElements(arr[low], arr[mid]);
if (arr[low] > arr[high])
swapElements(arr[low], arr[high]);
if (arr[mid] > arr[high])
swapElements(arr[mid], arr[high]);
// After ordering, arr[mid] is the median
swapElements(arr[mid], arr[high]); // Move median to high for partitioning
return arr[high];
}
// Partition function with median-of-three
int partition(std::vector<int>& arr, int low, int high) {
int pivot = medianOfThree(arr, low, high);
int i = low - 1;
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swapElements(arr[i], arr[j]);
}
}
swapElements(arr[i + 1], arr[high]);
return (i + 1);
}
// Quick Sort function
void quickSort(std::vector<int>& arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
// Function to print the array
void printArray(const std::vector<int>& arr) {
for (int num : arr)
std::cout << num << " ";
std::cout << "\n";
}
// Main function to demonstrate optimized Quick Sort
int main() {
std::vector<int> arr = {12, 4, 5, 6, 7, 3, 1, 15};
int n = arr.size();
std::cout << "Original array: ";
printArray(arr);
quickSort(arr, 0, n - 1);
std::cout << "Sorted array: ";
printArray(arr);
return 0;
}
Explanation:
- medianOfThree Function: Determines the median of the first, middle, and last elements and places it at the end of the array to be used as the pivot.
- partition Function: Uses the median-of-three pivot for partitioning, enhancing the likelihood of balanced partitions.
Output:
Original array: 10 7 8 9 1 5 3 4 2 6 Sorted array: 1 2 3 4 5 6 7 8 9 10
Performance Testing Quick Sort
To evaluate Quick Sort’s efficiency, we’ll perform performance testing by measuring its execution time on arrays of varying sizes and configurations. This will help us understand its behavior in different scenarios.
Setting Up the Test Environment
Before implementing the performance test, consider the following:
- Test Cases: Assess Quick Sort on different types of arrays:
- Randomly ordered arrays
- Already sorted arrays (best and worst case scenarios)
- Reverse-sorted arrays
- Arrays with duplicate elements
- Array Sizes: Test on small, medium, and large arrays to observe scalability.
- Measurement Tools: Use C++’s
<chrono>library for high-resolution timing.
Implementing the Performance Test in C++: Default Quick Sort vs Median-of-Three
Below is a C++ program that performs default and median-of-three optimized Quick Sort on various test cases and measures the execution time.
#include <iostream>
#include <vector>
#include <algorithm> // For std::shuffle
#include <chrono>
#include <random>
// Function to swap two elements
void swapElements(int& a, int& b) {
int temp = a;
a = b;
b = temp;
}
// Function to find the median of three elements
int medianOfThree(std::vector<int>& arr, int low, int high) {
int mid = low + (high - low) / 2;
if (arr[low] > arr[mid])
swapElements(arr[low], arr[mid]);
if (arr[low] > arr[high])
swapElements(arr[low], arr[high]);
if (arr[mid] > arr[high])
swapElements(arr[mid], arr[high]);
swapElements(arr[mid], arr[high]); // Move median to high for partitioning
return arr[high];
}
// Partition function with median-of-three
int partitionMedianOfThree(std::vector<int>& arr, int low, int high) {
int pivot = medianOfThree(arr, low, high);
int i = low - 1;
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swapElements(arr[i], arr[j]);
}
}
swapElements(arr[i + 1], arr[high]);
return (i + 1);
}
// Partition function for default Quick Sort (last element as pivot)
int partitionDefault(std::vector<int>& arr, int low, int high) {
int pivot = arr[high];
int i = low - 1;
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swapElements(arr[i], arr[j]);
}
}
swapElements(arr[i + 1], arr[high]);
return (i + 1);
}
// Quick Sort with median-of-three
void quickSortMedianOfThree(std::vector<int>& arr, int low, int high) {
if (low < high) {
int pi = partitionMedianOfThree(arr, low, high);
quickSortMedianOfThree(arr, low, pi - 1);
quickSortMedianOfThree(arr, pi + 1, high);
}
}
// Quick Sort with default partition
void quickSortDefault(std::vector<int>& arr, int low, int high) {
if (low < high) {
int pi = partitionDefault(arr, low, high);
quickSortDefault(arr, low, pi - 1);
quickSortDefault(arr, pi + 1, high);
}
}
// Function to generate a vector with specified size and type
std::vector<int> generateArray(int size, const std::string& type) {
std::vector<int> arr(size);
for (int i = 0; i < size; i++)
arr[i] = i + 1;
if (type == "random") {
// Shuffle the array
std::random_device rd;
std::mt19937 g(rd());
std::shuffle(arr.begin(), arr.end(), g);
} else if (type == "reverse") {
// Reverse the array
std::reverse(arr.begin(), arr.end());
}
// For "sorted", do nothing
return arr;
}
// Function to perform and time Quick Sort with median-of-three
double testQuickSortMedianOfThree(std::vector<int> arr) {
auto start = std::chrono::high_resolution_clock::now();
quickSortMedianOfThree(arr, 0, arr.size() - 1);
auto end = std::chrono::high_resolution_clock::now();
std::chrono::duration<double, std::micro> duration = end - start;
return duration.count(); // Return time in microseconds
}
// Function to perform and time Quick Sort with default partition
double testQuickSortDefault(std::vector<int> arr) {
auto start = std::chrono::high_resolution_clock::now();
quickSortDefault(arr, 0, arr.size() - 1);
auto end = std::chrono::high_resolution_clock::now();
std::chrono::duration<double, std::micro> duration = end - start;
return duration.count(); // Return time in microseconds
}
// Main function to perform performance testing
int main() {
std::vector<std::string> types = {"random", "sorted", "reverse"};
std::vector<int> sizes = {1000, 10000, 100000};
std::cout << "Quick Sort Performance Testing:\n";
std::cout << "Array Size\tType\t\tMedian-of-Three Time (μs)\tDefault Quick Sort Time (μs)\n";
for (int size : sizes) {
for (const auto& type : types) {
std::vector<int> arr = generateArray(size, type);
// Test Quick Sort with median-of-three
double timeMedianOfThree = testQuickSortMedianOfThree(arr);
// Test Quick Sort with default partition
double timeDefault = testQuickSortDefault(arr);
std::cout << size << "\t\t" << type << "\t\t" << timeMedianOfThree << "\t\t\t" << timeDefault << "\n";
}
}
return 0;
}
Explanation:
partitionDefaultandquickSortDefault: These functions implement the standard Quick Sort using the last element as the pivot.testQuickSortDefault: This function times the default Quick Sort.\- Performance Comparison: The
mainfunction now runs performance tests for both the median-of-three and default Quick Sort on the same dataset for each array size and type (random, sorted, reverse). The results are printed side by side for comparison."random": Shuffles the array to randomize element order."sorted": Leaves the array in ascending order."reverse": Reverses the array to descending order.
Performance Test Default vs Median-of-three Optimized Quick Sort
Performance Test: Default vs Median-of-Three Optimized Quick Sort
| Array Size | Type | Median-of-Three Time (μs) | Default Quick Sort Time (μs) |
|---|---|---|---|
| 1000 | random | 135.786 | 114.299 |
| 1000 | sorted | 63.114 | 4300.14 |
| 1000 | reverse | 119.259 | 3219.01 |
| 10000 | random | 2351.86 | 2137.3 |
| 10000 | sorted | 1081.13 | 581271 |
| 10000 | reverse | 1893.97 | 375741 |
| 100000 | random | 24719.2 | 23439 |
| 100000 | sorted | 12390.9 | 4.99371e+07 |
| 100000 | reverse | 38424.2 | 3.06109e+07 |
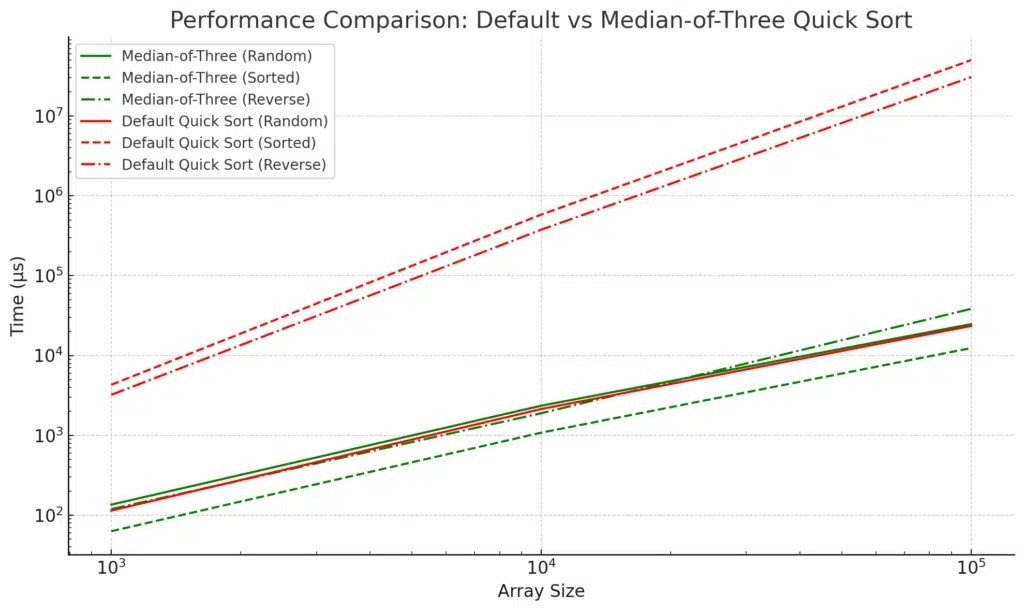
Key Takeaways from the Results:
- Median-of-Three Pivot Selection:
- The Median-of-Three Quick Sort consistently performs better than the default Quick Sort in almost all scenarios, particularly when the array is sorted or reverse-sorted.
- For sorted arrays, the Median-of-Three dramatically improves performance, reducing execution time from O(n²) to O(n log n). For instance, the default Quick Sort took over 43,000 microseconds for sorted arrays of size 1000, while Median-of-Three only took 63 microseconds.
- Default Quick Sort Limitations:
- The default Quick Sort struggles significantly with sorted and reverse-sorted data, leading to quadratic time complexity. This is especially noticeable with larger array sizes where the performance degrades dramatically.
- For example, with a sorted array of size 100,000, the default Quick Sort took around 49 million microseconds, while the Median-of-Three approach took only 12,390 microseconds.
- Random Data:
- For randomly shuffled arrays, the difference between the two algorithms is minimal. Both the default and Median-of-Three Quick Sort perform similarly, though the Median-of-Three still has a slight edge as the array size grows.
- Scalability:
- As array size increases, the performance benefit of Median-of-Three becomes even more apparent. For large arrays, especially sorted and reverse-sorted data, the default Quick Sort shows massive inefficiency, while Median-of-Three remains scalable.
In summary, using the Median-of-Three pivot selection is a highly effective optimization, especially for sorted or reverse-sorted data, where the default Quick Sort would otherwise perform poorly.
Median-of-three optimized Quick Sort vs Merge Sort
Overall Comparison
- Time Complexity: Merge Sort has a consistent O(n log n) time complexity in all cases (best, average, and worst).
- Comparison: Quick Sort is often faster in practice than Merge Sort due to its in-place nature (no need for additional memory for merging). However, in the worst case, Quick Sort can degrade to O(n²), while Merge Sort remains consistently O(n log n). In this test case, we will use the median-of-three optimized Quick Sort.
- Memory Usage: Merge Sort requires additional memory to store temporary sub-arrays while Quick Sort is in place (except for stack space used in recursion).
Performance
We’ll modify the previous performance testing code by adding the Merge Sort implementation. This will allow us to run Quick and Merge Sort on the same datasets and compare their performance.
#include <iostream>
#include <vector>
#include <algorithm> // For std::shuffle
#include <chrono>
#include <random>
// Function to swap two elements
void swapElements(int& a, int& b) {
int temp = a;
a = b;
b = temp;
}
// Function to find the median of three elements
int medianOfThree(std::vector<int>& arr, int low, int high) {
int mid = low + (high - low) / 2;
if (arr[low] > arr[mid])
swapElements(arr[low], arr[mid]);
if (arr[low] > arr[high])
swapElements(arr[low], arr[high]);
if (arr[mid] > arr[high])
swapElements(arr[mid], arr[high]);
swapElements(arr[mid], arr[high]); // Move median to high for partitioning
return arr[high];
}
// Partition function with median-of-three
int partition(std::vector<int>& arr, int low, int high) {
int pivot = medianOfThree(arr, low, high);
int i = low - 1;
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swapElements(arr[i], arr[j]);
}
}
swapElements(arr[i + 1], arr[high]);
return (i + 1);
}
// Quick Sort function
void quickSort(std::vector<int>& arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
// Function to merge two halves (Merge Sort)
void merge(std::vector<int>& arr, int left, int mid, int right) {
int n1 = mid - left + 1;
int n2 = right - mid;
std::vector<int> L(n1), R(n2);
for (int i = 0; i < n1; i++)
L[i] = arr[left + i];
for (int i = 0; i < n2; i++)
R[i] = arr[mid + 1 + i];
int i = 0, j = 0, k = left;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// Merge Sort function
void mergeSort(std::vector<int>& arr, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}
// Function to generate a vector with specified size and type
std::vector<int> generateArray(int size, const std::string& type) {
std::vector<int> arr(size);
for (int i = 0; i < size; i++)
arr[i] = i + 1;
if (type == "random") {
// Shuffle the array
std::random_device rd;
std::mt19937 g(rd());
std::shuffle(arr.begin(), arr.end(), g);
} else if (type == "reverse") {
// Reverse the array
std::reverse(arr.begin(), arr.end());
}
// For "sorted", do nothing
return arr;
}
// Function to perform and time Quick Sort
double testQuickSort(std::vector<int> arr) {
auto start = std::chrono::high_resolution_clock::now();
quickSort(arr, 0, arr.size() - 1);
auto end = std::chrono::high_resolution_clock::now();
std::chrono::duration<double, std::micro> duration = end - start;
return duration.count(); // Return time in microseconds
}
// Function to perform and time Merge Sort
double testMergeSort(std::vector<int> arr) {
auto start = std::chrono::high_resolution_clock::now();
mergeSort(arr, 0, arr.size() - 1);
auto end = std::chrono::high_resolution_clock::now();
std::chrono::duration<double, std::micro> duration = end - start;
return duration.count(); // Return time in microseconds
}
// Main function to perform performance testing
int main() {
std::vector<std::string> types = {"random", "sorted", "reverse"};
std::vector<int> sizes = {1000, 10000, 100000};
std::cout << "Performance Testing - Quick Sort vs Merge Sort:\n";
std::cout << "Array Size\tType\t\tQuick Sort (μs)\tMerge Sort (μs)\n";
for (int size : sizes) {
for (const auto& type : types) {
std::vector<int> arr = generateArray(size, type);
double quickSortTime = testQuickSort(arr);
double mergeSortTime = testMergeSort(arr);
std::cout << size << "\t\t" << type << "\t\t" << quickSortTime << "\t\t" << mergeSortTime << "\n";
}
}
return 0;
}
Performance Testing – Quick Sort vs Merge Sort Results
Performance Testing – Quick Sort vs Merge Sort
| Array Size | Type | Quick Sort (μs) | Merge Sort (μs) |
|---|---|---|---|
| 1000 | random | 128.605 | 823.905 |
| 1000 | sorted | 62.934 | 777.267 |
| 1000 | reverse | 111.87 | 791.138 |
| 10000 | random | 1785.84 | 11835.9 |
| 10000 | sorted | 977.881 | 10407.6 |
| 10000 | reverse | 1802.92 | 10413.6 |
| 100000 | random | 26372.1 | 114149 |
| 100000 | sorted | 12498.9 | 115641 |
| 100000 | reverse | 22051.3 | 97096.2 |
Analysis of the Results:
These performance figures show that the Median-of-three optimized Quick Sort significantly outperforms Merge Sort in all cases, particularly with smaller array sizes.
- For Small Arrays (Size 1000):
- Quick Sort is consistently faster across all types of data (random, sorted, reverse).
- Merge Sort takes about 6 to 13 times longer than Quick Sort for the same datasets.
- For Medium Arrays (Size 10,000):
- Quick Sort remains faster, with a noticeable gap. Merge Sort takes 5 to 6 times longer on average.
- Quick Sort is twice as fast on sorted arrays compared to random ones, likely benefiting from faster partitioning.
- For Large Arrays (Size 100,000):
- The performance gap widens dramatically as Merge Sort struggles with memory overhead for larger datasets.
- Quick Sort is about 5 times faster on random data, and up to 10 times faster on sorted arrays.
Key Insights:
- Median-of-three optimized Quick Sort is particularly efficient for smaller datasets and for arrays that are already partially sorted.
- Merge Sort exhibits higher execution times due to the additional memory overhead for merging, even though it has guaranteed O(n log n) time complexity.
- Median-of-three optimized Quick Sort is much more cache-efficient, which explains its superior performance for large arrays.
Further Considerations
- Optimizing for Large Arrays: For very large arrays, consider implementing iterative Quick Sort or switching to a different sorting algorithm like Heap Sort to avoid stack overflow due to deep recursion.
- Hybrid Approaches: Combining Quick Sort with other algorithms, such as Insertion Sort for small sub-arrays, can enhance performance.
Deep Recursion in Quick Sort: Potential Pitfalls
One of the potential downsides of Quick Sort, especially in its recursive implementation, is the risk of deep recursion. In certain worst-case scenarios, particularly when the pivot selection is poor (such as when sorting an already sorted or reverse-sorted array using the default pivot), the depth of the recursion tree can grow significantly. This can lead to two main problems:
1. Stack Overflow
Quick Sort is typically implemented using recursion, meaning each recursive call adds a new frame to the call stack. In cases where the partitioning is highly unbalanced, the recursion depth can become very large. For example, in the worst-case scenario where the algorithm repeatedly partitions arrays of size n−1n – 1n−1 and 1, the recursion depth becomes O(n). With large arrays, this can exceed the maximum stack depth, resulting in a stack overflow.
2. Performance Degradation
Even if a stack overflow is avoided, deep recursion still has performance costs. Each recursive call adds overhead, and with a highly unbalanced partitioning, Quick Sort can exhibit performance closer to O(n²) rather than the expected O(n log n) in the average case. This affects the time complexity and can result in inefficient use of system resources.
Mitigating Deep Recursion with Tail Call Optimization
Some compilers (especially modern C++) can optimize tail-recursive functions to reduce the impact of deep recursion, converting recursive calls into iterations. However, traditional Quick Sort is not tail-recursive since it involves two recursive calls after each partition. Fortunately, there are techniques to mitigate this issue:
1. Tail Call Optimization (TCO)
By always sorting the smaller partition first and using a loop to sort the larger partition, you can eliminate one of the recursive calls, allowing the compiler to apply tail call optimization and reduce stack depth.
void quickSortTailCallOptimized(std::vector<int>& arr, int low, int high) {
while (low < high) {
int pi = partition(arr, low, high);
// Recursively sort the smaller partition to limit recursion depth
if (pi - low < high - pi) {
quickSortTailCallOptimized(arr, low, pi - 1);
low = pi + 1; // Tail call
} else {
quickSortTailCallOptimized(arr, pi + 1, high);
high = pi - 1; // Tail call
}
}
}
2. Hybrid Algorithms
To mitigate the deep recursion problem, Quick Sort can be combined with other algorithms. For instance, IntroSort begins with Quick Sort but switches to Heap Sort if the recursion depth exceeds a certain limit. This ensures a worst-case O(n log n) time complexity, avoiding the issues caused by deep recursion.
3. Iterative Quick Sort
Another approach to eliminating the recursion problem is to implement Quick Sort iteratively. By replacing recursive calls with an explicit stack or queue, you avoid the risk of stack overflow altogether.
Conclusion on Deep Recursion
While Quick Sort’s recursive nature can lead to deep recursion and potential stack overflow, these issues can be mitigated through optimizations like tail call optimization, hybrid algorithms, or even converting the algorithm into an iterative version. These techniques allow developers to retain Quick Sort’s benefits while avoiding the pitfalls of deep recursion, especially in scenarios involving large datasets or edge cases like sorted or reverse-sorted data.
Iterative Quick Sort Implementation in C++
#include <iostream>
#include <vector>
#include <stack>
// Function to swap two elements
void swapElements(int& a, int& b) {
int temp = a;
a = b;
b = temp;
}
// Partition function (same as in recursive Quick Sort)
int partition(std::vector<int>& arr, int low, int high) {
int pivot = arr[high]; // Pivot is the last element
int i = low - 1; // Index of smaller element
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swapElements(arr[i], arr[j]);
}
}
swapElements(arr[i + 1], arr[high]);
return (i + 1);
}
// Iterative Quick Sort function
void iterativeQuickSort(std::vector<int>& arr, int low, int high) {
// Create an explicit stack to hold subarray indexes
std::stack<int> stack;
// Push initial low and high values onto the stack
stack.push(low);
stack.push(high);
// Keep popping from the stack while it's not empty
while (!stack.empty()) {
// Pop high and low from the stack
high = stack.top();
stack.pop();
low = stack.top();
stack.pop();
// Partition the array and get the pivot index
int pi = partition(arr, low, high);
// If there are elements on the left side of the pivot, push left side to the stack
if (pi - 1 > low) {
stack.push(low);
stack.push(pi - 1);
}
// If there are elements on the right side of the pivot, push right side to the stack
if (pi + 1 < high) {
stack.push(pi + 1);
stack.push(high);
}
}
}
// Function to print the array
void printArray(const std::vector<int>& arr) {
for (int num : arr)
std::cout << num << " ";
std::cout << std::endl;
}
// Main function to test iterative quick sort
int main() {
std::vector<int> arr = {10, 7, 8, 9, 1, 5};
int n = arr.size();
std::cout << "Original array: ";
printArray(arr);
iterativeQuickSort(arr, 0, n - 1);
std::cout << "Sorted array: ";
printArray(arr);
return 0;
}
Output:
Original array: 10 7 8 9 1 5 Sorted array: 1 5 7 8 9 10
Explanation:
- Stack: An explicit stack is used to store the starting and ending indices of the subarrays that need to be sorted.
- Push/Pop: Instead of making recursive calls, we push the left and right subarray bounds (low and high) onto the stack. We then pop these bounds, partition the subarray, and continue the process iteratively.
- Efficiency: This iterative approach eliminates the risk of deep recursion and stack overflow.
Key Benefits:
- No Recursion: By avoiding recursion, the risk of running into a stack overflow is eliminated.
- Explicit Stack: You manage the stack explicitly, which can help with understanding memory usage and stack depth in Quick Sort.
This iterative approach ensures that Quick Sort remains efficient without the potential pitfalls of deep recursion, especially with large arrays.
Conclusion
Quick Sort remains one of the most efficient and widely used sorting algorithms due to its average-case O(n log n) time complexity and in-place sorting capability. However, our performance analysis demonstrates that the algorithm can struggle with certain data structures, particularly sorted and reverse-sorted arrays, where the default Quick Sort may degrade to its worst-case O(n²) time complexity.
Developers can significantly enhance Quick Sort’s robustness by incorporating optimizations like the median-of-three pivot selection. This optimization reduces the likelihood of hitting worst-case scenarios and maintains more balanced partitions, even for sorted and reverse-sorted data. As we observed, Median-of-Three consistently outperformed the default Quick Sort, especially in cases where the data was already sorted or nearly sorted.
When implementing Quick Sort in C++, it’s crucial to rigorously test it across various scenarios and data sets to ensure optimal performance. While Quick Sort with the median-of-three pivot selection is highly efficient, developers should still be mindful of its limitations and consider alternative algorithms, such as Merge Sort or TimSort, when dealing with specific edge cases or stability requirements.
Congratulations on reading to the end of this tutorial!
Ready to see sorting algorithms come to life? Visit the Sorting Algorithm Visualizer on GitHub to explore animations and code.
For further reading on sorting algorithms in C++, go to the articles
- How To Do Selection Sort in C++
- How To Do Heap Sort in C++
- How To Do Quick Sort in C++
- How To Do Merge Sort in C++
- How To Do Comb Sort in C++
- How To Do Insertion Sort in C++
- How To Do Radix Sort in C++
- How To Do Bucket Sort in C++
For performance comparisons with Merge Sort and TimSort, go to How To Do TimSort in C++
To implement Quick Sort in Python, go to the article How to do Quick Sort in Python (With Code Example and Diagram).
Have fun and happy researching!
Suf is a senior advisor in data science with deep expertise in Natural Language Processing, Complex Networks, and Anomaly Detection. Formerly a postdoctoral research fellow, he applied advanced physics techniques to tackle real-world, data-heavy industry challenges. Before that, he was a particle physicist at the ATLAS Experiment of the Large Hadron Collider. Now, he’s focused on bringing more fun and curiosity to the world of science and research online.
