Results
Understanding Roulette: A Complete Guide
Roulette is a classic casino game that comes in two main variants: European (37 numbers) and American (38 numbers). The key difference? American roulette adds a double zero (00), which increases the house edge from 2.7% to 5.26%. Each number is associated with either red, black, or green (for 0 and 00), creating a visual and statistical distinction. From a probability perspective, the additional zero shifts the likelihood of winning bets slightly in favor of the house, making the American version statistically less favorable for players. Understanding this subtle probability difference is crucial for making informed bets and maximizing returns over time.
European Roulette Wheel:
37 numbers (0-36)Single zero (0)
House Edge: 2.7%
Better odds for players
American Roulette Wheel
38 numbers (0-36, 00)Double zero (00)
House Edge: 5.26%
Higher house advantage
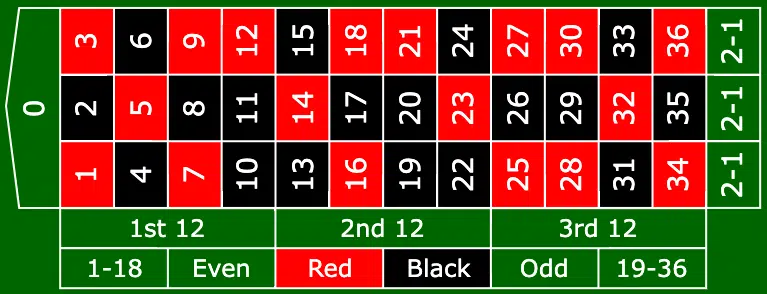
European Roulette Table
37 numbers (0-36)Single zero (0)
House Edge: 2.7%
Better odds for players
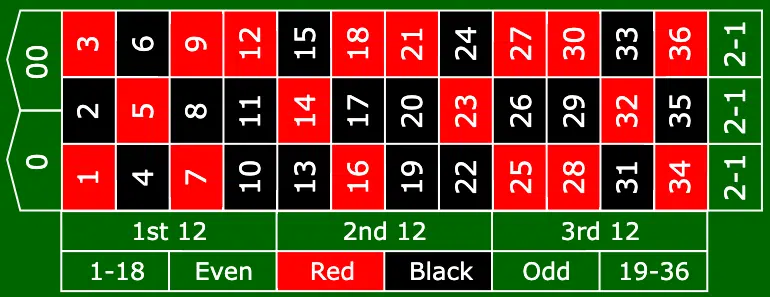
American Roulette Table
38 numbers (0-36, 00)Double zero (00)
House Edge: 5.26%
Higher house advantage
Complete Roulette Odds Comparison
| Bet Type | Numbers Covered | Probability | Payout | House Edge |
|---|---|---|---|---|
| Red/Black | 18 | 48.65% (18/37) | 1:1 | -2.70% |
| Even/Odd | 18 | 48.65% (18/37) | 1:1 | -2.70% |
| 1-18/19-36 | 18 | 48.65% (18/37) | 1:1 | -2.70% |
| Dozens | 12 | 32.43% (12/37) | 2:1 | -2.70% |
| Column | 12 | 32.43% (12/37) | 2:1 | -2.70% |
| Double Street | 6 | 16.22% (6/37) | 5:1 | -2.70% |
| Corner | 4 | 10.81% (4/37) | 8:1 | -2.70% |
| Street | 3 | 8.11% (3/37) | 11:1 | -2.70% |
| Split | 2 | 5.41% (2/37) | 17:1 | -2.70% |
| Straight | 1 | 2.70% (1/37) | 35:1 | -2.70% |
| Bet Type | Numbers Covered | Probability | Payout | House Edge |
|---|---|---|---|---|
| Red/Black | 18 | 47.37% (18/38) | 1:1 | -5.26% |
| Even/Odd | 18 | 47.37% (18/38) | 1:1 | -5.26% |
| 1-18/19-36 | 18 | 47.37% (18/38) | 1:1 | -5.26% |
| Dozens | 12 | 31.58% (12/38) | 2:1 | -5.26% |
| Column | 12 | 31.58% (12/38) | 2:1 | -5.26% |
| Double Street | 6 | 15.79% (6/38) | 5:1 | -5.26% |
| Corner | 4 | 10.53% (4/38) | 8:1 | -5.26% |
| Street | 3 | 7.89% (3/38) | 11:1 | -5.26% |
| Split | 2 | 5.26% (2/38) | 17:1 | -5.26% |
| Straight | 1 | 2.63% (1/38) | 35:1 | -5.26% |
Frequently Asked Questions (FAQs)
How do you calculate odds in roulette?
To calculate the odds of a bet in roulette, divide the number of winning outcomes by the total number of possible outcomes. For example, in European roulette:
- Straight Up Bet (Single Number): \( \frac{1}{37} \) or approximately \( 2.7\% \).
- Red/Black Bet: \( \frac{18}{37} \) or approximately \( 48.6\% \).
In American roulette, the calculation is similar but with 38 total numbers, reducing the odds slightly due to the additional double zero (\( 00 \)).
What is the house edge in roulette?
The house edge represents the casino’s statistical advantage. It is calculated as:
\[ \text{House Edge} = 1 – (\text{Winning Probability} \times \text{Payout Ratio}) \]The payout ratio is the multiplier applied to your bet if you win. It reflects the reward for a successful bet relative to the bet amount. For example:
- Straight Up Bet: Payout ratio is \( 35:1 \), meaning you receive 35 times your bet amount in winnings.
- Red/Black Bet: Payout ratio is \( 1:1 \), meaning you receive 1 times your bet amount in winnings.
The payout ratio formula can be expressed as:
\[ \text{Payout Ratio} = \frac{\text{Number of Total Numbers}}{\text{Number of Winning Numbers}} – 1 \]For European roulette, the house edge is approximately \( 2.7\% \). For American roulette, with the extra double zero (\( 00 \)), the house edge increases to \( 5.26\% \).
What is the expected value (EV) in roulette?
The expected value (EV) helps you understand how much money you can expect to win or lose on average if you place the same bet many times. It’s like figuring out whether the game is in your favor or the casino’s.
Imagine you’re flipping a coin, but instead of it being fair, it’s slightly rigged against you. The EV tells you how much you’re likely to lose each time you flip the coin. In roulette, the EV works the same way, but the “rigging” comes from the house edge.
The formula for EV is:
\[ EV = (\text{Winning Probability} \times \text{Payout}) – (\text{Losing Probability} \times \text{Bet Amount}) \]Let’s break it down with a Straight Up bet in European roulette (betting on a single number):
- Winning Probability: \( \frac{1}{37} \) (because there’s 1 winning number out of 37).
- Payout: \( 35:1 \) (if you win, you get 35 times your bet).
- Losing Probability: \( \frac{36}{37} \) (because there are 36 ways to lose).
Plugging these into the formula:
\[ EV = \left( \frac{1}{37} \times 35 \right) – \left( \frac{36}{37} \times 1 \right) \]This gives:
\[ EV = 0.945 – 0.973 = -0.027 \]So, on average, you lose 2.7% of your bet amount every time you make this bet. For example, if you bet \$100, you’d lose about \$2.70 on average over many bets.
A negative EV means the game is designed to favor the casino (this is called the house edge). While you might win some bets, the casino is statistically guaranteed to win more over time.
What are the payouts for different roulette bets?
Here are the payouts for the most common roulette bets:
- Straight Up (Single Number): \( 35:1 \)
- Split (Two Numbers): \( 17:1 \)
- Street (Three Numbers): \( 11:1 \)
- Corner (Four Numbers): \( 8:1 \)
- Six Line (Six Numbers): \( 5:1 \)
- Column/Dozens (12 Numbers): \( 2:1 \)
- Red/Black, Even/Odd, High/Low (18 Numbers): \( 1:1 \)
What is the difference between European and American roulette?
The primary difference is the total number of outcomes:
- European Roulette: 37 numbers (\( 0-36 \)) with a single zero (\( 0 \)). House Edge: \( 2.7\% \).
- American Roulette: 38 numbers (\( 0-36 \) and \( 00 \)) with an additional double zero (\( 00 \)). House Edge: \( 5.26\% \).
The extra \( 00 \) in American roulette increases the house edge, making it less favorable for players compared to the European version.
What is the difference between inside bets and outside bets?
Inside bets are placed on specific numbers or groups of numbers on the roulette table, such as straight-up bets, split bets, street bets, corner bets, and six-line bets. These bets offer higher payouts but have lower probabilities of winning.
Outside bets are placed on larger categories of numbers, such as red/black, even/odd, high/low, and dozens. These bets have lower payouts but higher probabilities of winning.
What does Red/Black mean in roulette?
A Red/Black bet is placed on whether the ball will land on a red or black number. There are 18 red and 18 black numbers, excluding the green zero(s). The probability of winning is:
\[ \text{Winning Probability} = \frac{18}{37} \approx 48.65\% \]This bet pays 1:1 and has a house edge of \( -2.70\% \) in European roulette.
What does Even/Odd mean in roulette?
A Even/Odd bet is placed on whether the ball will land on an even or odd number. There are 18 even and 18 odd numbers, excluding the zero(s). The probability of winning is:
\[ \text{Winning Probability} = \frac{18}{37} \approx 48.65\% \]This bet pays 1:1 and has a house edge of \( -2.70\% \).
What does 1-18/19-36 mean in roulette?
A 1-18/19-36 bet, also called High/Low, is placed on whether the ball will land on a low number (1-18) or a high number (19-36). The probability of winning is:
\[ \text{Winning Probability} = \frac{18}{37} \approx 48.65\% \]This bet pays 1:1 and has a house edge of \( -2.70\% \).
What does Dozens mean in roulette?
A Dozens bet is placed on one of three groups of 12 numbers: 1-12, 13-24, or 25-36. The probability of winning is:
\[ \text{Winning Probability} = \frac{12}{37} \approx 32.43\% \]This bet pays 2:1 and has a house edge of \( -2.70\% \).
What does Column mean in roulette?
A Column bet is placed on one of three vertical columns of numbers on the roulette table. Each column contains 12 numbers. The probability of winning is:
\[ \text{Winning Probability} = \frac{12}{37} \approx 32.43\% \]This bet pays 2:1 and has a house edge of \( -2.70\% \).
What does Double Street mean in roulette?
A Double Street bet, also called a Six Line bet, is placed on two adjacent rows of three numbers (six numbers in total). The probability of winning is:
\[ \text{Winning Probability} = \frac{6}{37} \approx 16.22\% \]This bet pays 5:1 and has a house edge of \( -2.70\% \).
What does Corner mean in roulette?
A Corner bet, also called a Square bet, is placed on four numbers that form a square on the table layout. The probability of winning is:
\[ \text{Winning Probability} = \frac{4}{37} \approx 10.81\% \]This bet pays 8:1 and has a house edge of \( -2.70\% \).
What does Street mean in roulette?
A Street bet is placed on a row of three numbers (e.g., 1-2-3). The probability of winning is:
\[ \text{Winning Probability} = \frac{3}{37} \approx 8.11\% \]This bet pays 11:1 and has a house edge of \( -2.70\% \).
What does Split mean in roulette?
A Split bet is placed on two adjacent numbers (e.g., 1 and 2). The probability of winning is:
\[ \text{Winning Probability} = \frac{2}{37} \approx 5.41\% \]This bet pays 17:1 and has a house edge of \( -2.70\% \).
What does Straight mean in roulette?
A Straight Up bet is placed on a single number (e.g., 7). The probability of winning is:
\[ \text{Winning Probability} = \frac{1}{37} \approx 2.70\% \]This bet pays 35:1 and has a house edge of \( -2.70\% \).
Attribution
If you found this guide and tools helpful, feel free to link back to this page for attribution and share it with others!
Feel free to use these formats to reference our tools in your articles, blogs, or websites.
Further Reading
If you’re interested in exploring more about roulette, its mathematical principles, and probability concepts, check out the following resources:
- Wikipedia: Roulette – A comprehensive overview of the game, its history, and rules.
- The Research Scientist Pod Calculators – Dive into our suite of probability calculators, including:
- Union and Intersection Probability Calculator – Calculate the probabilities of combined events.
- Probability of at Least One Success Calculator – Find the probability of success in repeated trials.
- Markov Chain Calculator – Analyze state transitions using Markov chains.
Suf is a senior advisor in data science with deep expertise in Natural Language Processing, Complex Networks, and Anomaly Detection. Formerly a postdoctoral research fellow, he applied advanced physics techniques to tackle real-world, data-heavy industry challenges. Before that, he was a particle physicist at the ATLAS Experiment of the Large Hadron Collider. Now, he’s focused on bringing more fun and curiosity to the world of science and research online.