When conducting multiple statistical tests, the chance of obtaining false-positive results increases significantly. The Bonferroni correction is a simple yet powerful method to control this familywise error rate. In this guide, we’ll walk through implementing this correction in R, complete with practical examples and visualizations.
Table of Contents
Understanding Bonferroni Correction
The Bonferroni correction helps us maintain control over Type I errors (false positives) when performing multiple statistical tests. It’s particularly useful in scenarios where we’re comparing multiple groups or testing multiple hypotheses simultaneously. While it’s considered conservative, its simplicity and effectiveness make it a popular choice in many fields, from biology to psychology.
The Bonferroni Formula
The Bonferroni correction adjusts the significance level (\(\alpha\)) for each individual test by dividing the desired overall \(\alpha\) level by the number of comparisons being made. The formula is straightforward:
\[ \alpha_{\text{adjusted}} = \frac{\alpha}{n} \]
Where:
- \(\alpha\) is the original significance level (typically 0.05)
- \(n\) is the number of comparisons being made
- \(\alpha_{\text{adjusted}}\) is the new significance threshold for each individual test
Let’s understand this with a practical example: When comparing 4 groups, we need \(\binom{4}{2} = 6\) pairwise comparisons. If we start with an overall significance level of \(\alpha = 0.05\), each individual test would use an adjusted threshold of:
\[ \alpha_{\text{adjusted}} = \frac{0.05}{6} \approx 0.0083 \]
This stricter threshold helps maintain the familywise error rate at our desired level of 5% across all comparisons.
Creating Example Dataset
Let’s create a sample dataset to demonstrate the Bonferroni correction in action. We’ll simulate test scores from four different study methods:
# Set seed for reproducibility
set.seed(123)
# Create data frame with test scores from four study methods
data <- data.frame(
score = c(
rnorm(20, mean = 75, sd = 5), # Method A
rnorm(20, mean = 78, sd = 5), # Method B
rnorm(20, mean = 82, sd = 5), # Method C
rnorm(20, mean = 76, sd = 5) # Method D
),
method = factor(rep(c("A", "B", "C", "D"), each = 20))
)
head(data)1 72.19762 A
2 73.84911 A
3 82.79354 A
4 75.35254 A
5 75.64644 A
6 83.57532 A
Visualizing Groups
Before diving into the statistical analysis, it's always good practice to visualize our data. We'll create a boxplot using ggplot2 to see the distribution of scores across different study methods:
# Load required library
library(ggplot2)
# Create boxplot with centered title
ggplot(data, aes(x = method, y = score)) +
geom_boxplot(fill = "lightblue", alpha = 0.7) +
geom_jitter(width = 0.2, alpha = 0.5) +
theme_minimal() +
theme(
# Center the plot title
plot.title = element_text(hjust = 0.5)
) +
labs(
title = "Test Scores by Study Method",
x = "Study Method",
y = "Score"
)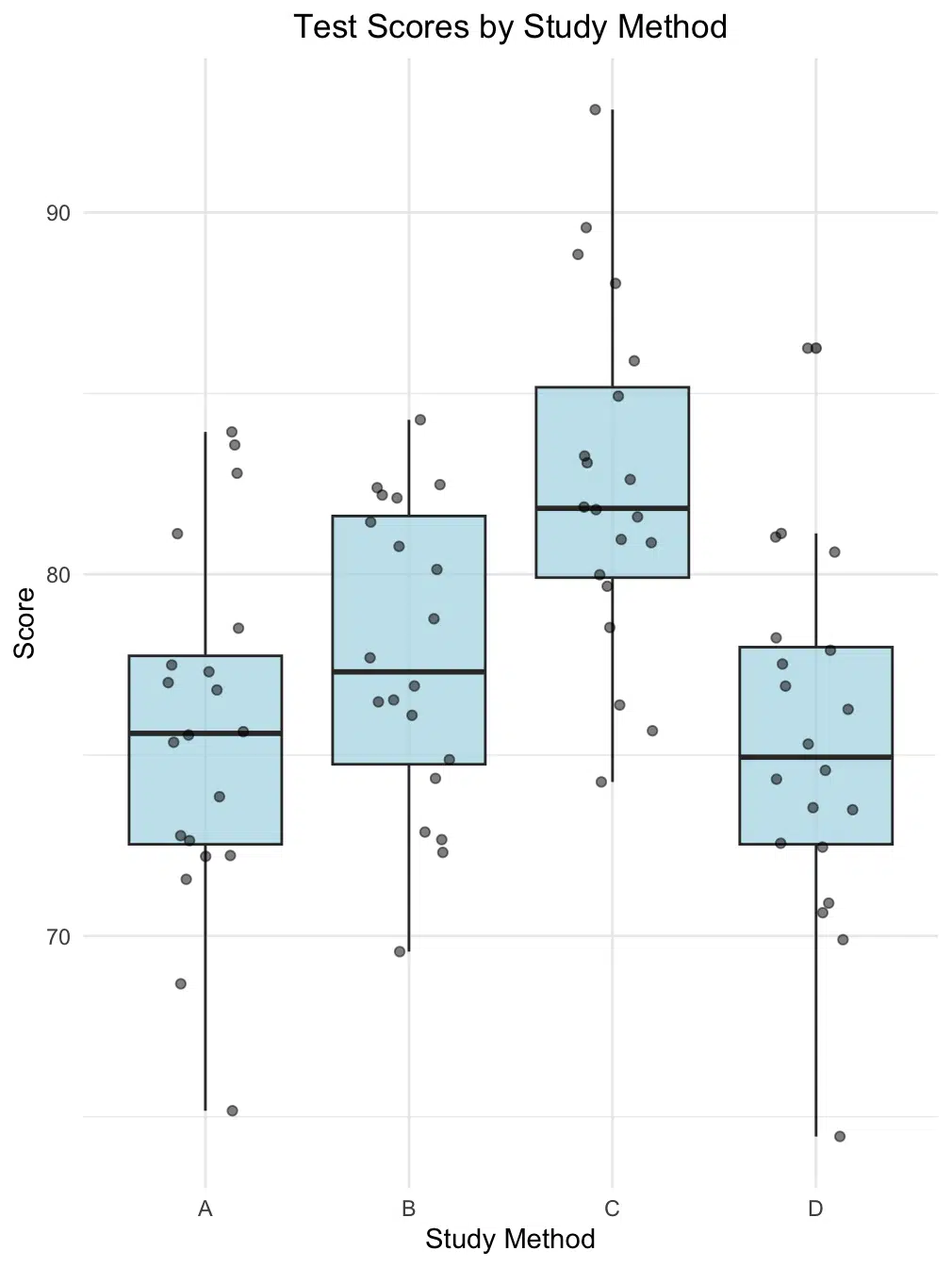
This visualization helps us identify several key patterns in our study method comparison. The box plots reveal the central tendency and spread of scores for each method, with Method C showing notably higher median scores. The overlaid individual data points help us understand the underlying distribution and identify any potential outliers. We can observe that while Method C appears to perform best overall, there is some overlap in score distributions between methods, highlighting the importance of our subsequent statistical analysis using Bonferroni correction. For a deeper understanding of boxplot interpretation or to create your own visualizations, you can explore our interactive box plot maker, which allows you to create and customize similar visualizations for your own data analysis needs.
Performing One-way ANOVA
Before conducting pairwise comparisons, we should first perform a one-way ANOVA to test if there are any significant differences between groups:
# Perform one-way ANOVA
anova_result <- aov(score ~ method, data = data)
summary(anova_result)Let's analyze the ANOVA results from our study methods comparison in detail:
method 3 650.5 216.83 9.917 1.36e-05 ***
Residuals 76 1661.7 21.86
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Breaking down the key components:
The method row shows 3 degrees of freedom (comparing 4 groups means 4-1 = 3 df), with a Sum of Squares of 650.5 and Mean Square of 216.83, indicating substantial variation between study methods.
The Residuals row with 76 degrees of freedom (from 20 students × 4 groups - 4) and Mean Square of 21.86 represents the natural variation within each study method.
The F-value of 9.917 (calculated as 216.83/21.86) reveals that the variation between methods is approximately 10 times larger than what we'd expect by chance, given the within-method variation.
The extremely small p-value (1.36e-05) indicates that these differences between study methods would be very rare if all methods were equally effective. This strong evidence justifies proceeding with pairwise comparisons using Bonferroni correction to identify specifically which methods differ from each other.
Pairwise Tests with Bonferroni Correction
Now we'll perform pairwise t-tests with Bonferroni correction to identify which specific groups differ from each other:
# Perform pairwise t-tests with Bonferroni correction
pairwise_result <- pairwise.t.test(
data$score,
data$method,
p.adjust.method = "bonferroni"
)
print(pairwise_result)The pairwise t-test results with Bonferroni correction reveal some fascinating patterns in our study method effectiveness. Let's break down these comparisons systematically:
data: data$score and data$method
A B C
B 1.000 - -
C 9.4e-05 0.011 -
D 1.000 0.703 4.3e-05
P value adjustment method: bonferroni
Looking at these results, Method C stands out dramatically from the others. Let's interpret each comparison:
Method C Comparisons:
- C vs. A: p = 9.4e-05 (highly significant)
- C vs. B: p = 0.011 (significant)
- C vs. D: p = 4.3e-05 (highly significant)
These extremely small p-values, even after Bonferroni correction, indicate that Method C consistently outperforms all other methods.
In contrast, the other methods show no significant differences between them:
- A vs. B: p = 1.000
- A vs. D: p = 1.000
- B vs. D: p = 0.703
These high p-values (close to or equal to 1) suggest that Methods A, B, and D produce similar results. Remember that these p-values have been adjusted using the Bonferroni correction, making them more conservative than unadjusted p-values to protect against Type I errors across multiple comparisons.
From a practical standpoint, these results suggest that if you're choosing between these study methods, Method C would be the recommended approach, as it demonstrates statistically superior performance compared to all alternatives. The other methods, while potentially useful, don't show meaningful differences in effectiveness from each other.
💡 Important Considerations:
- The Bonferroni correction is conservative, meaning it might miss some true differences (Type II errors)
- For a large number of comparisons, consider alternative methods like Holm's or Benjamini-Hochberg
- The correction assumes independence between tests
Conclusion
Understanding and properly implementing multiple comparison corrections is crucial for maintaining statistical rigor in your analyses. Throughout this guide, we've explored how the Bonferroni correction helps control the familywise error rate when conducting multiple statistical tests, providing a straightforward yet powerful method to avoid spurious significant results.
We've seen how to apply this correction in practice using R, starting from data preparation through visualization and finally to statistical testing. The example of comparing study methods demonstrated not only the technical implementation but also the practical interpretation of results. While our example showed significant differences between some study methods (particularly Method C compared to others), the Bonferroni correction helped ensure these differences weren't just statistical artifacts from multiple testing.
Remember that while the Bonferroni correction is one of the most widely used methods for controlling familywise error rate, it's important to consider your specific research context. For studies with a large number of comparisons, you might want to explore other methods like Holm's sequential procedure or the less conservative Benjamini-Hochberg method, which controls the false discovery rate instead. The key is balancing the risk of Type I errors (false positives) against the power to detect true differences in your data.
Moving forward with your own analyses, consider incorporating these practices:
- Always visualize your data before conducting statistical tests to understand the underlying patterns
- Consider the number of comparisons you'll be making early in your research design
- Document your choice of correction method and justify it based on your research goals
- Report both uncorrected and corrected p-values for transparency
- Interpret results in the context of your field and research questions
By following these guidelines and understanding the principles behind multiple comparison corrections, you'll be better equipped to conduct robust statistical analyses that stand up to scientific scrutiny. The Bonferroni correction, while simple in concept, remains a valuable tool in the modern statistician's toolkit, helping ensure that our discoveries represent genuine effects rather than statistical artifacts.
Further Reading
-
Interactive ANOVA Calculator
Our user-friendly ANOVA calculator allows you to perform Analysis of Variance calculations without writing code. Perfect for quickly testing group differences and validating your R analysis results, this tool provides both numerical outputs and visual representations of your data.
-
Bonferroni Correction Calculator
Complement your understanding by using our interactive Bonferroni correction calculator. This tool helps you quickly compute adjusted p-values for multiple comparisons, making it easier to understand how the correction affects your significance thresholds and interpret your results accurately.
-
R Documentation: p.adjust
The official R documentation for p-value adjustments provides detailed information about implementing different correction methods, including Bonferroni, Holm, and Benjamini-Hochberg procedures. This resource is essential for understanding the technical aspects of multiple comparison corrections in R.
Attribution and Citation
If you found this guide and tools helpful, feel free to link back to this page or cite it in your work!
Suf is a senior advisor in data science with deep expertise in Natural Language Processing, Complex Networks, and Anomaly Detection. Formerly a postdoctoral research fellow, he applied advanced physics techniques to tackle real-world, data-heavy industry challenges. Before that, he was a particle physicist at the ATLAS Experiment of the Large Hadron Collider. Now, he’s focused on bringing more fun and curiosity to the world of science and research online.

