How to Calculate Percentile Cutoff for Normal Distribution in R with Practical Examples

In statistics, calculating percentile cutoffs within a normal distribution can be extremely useful for defining thresholds for data analysis. This guide explains how to calculate percentile cutoffs in R, interpret them, and apply them to real-life use cases.

Introduction to Percentile Cutoffs

Percentile cutoffs indicate values where a certain proportion of the data falls below or above. For example, the 90th percentile represents the value below which 90% of data points lie, assuming a normal distribution. Percentile cutoffs are used in fields like finance, quality control, and academic assessments to set thresholds.

Understanding Percentiles in a Normal Distribution

In a normal distribution, percentile cutoffs are calculated based on the mean \( \mu \) and standard deviation \( \sigma \) of the dataset. For a normal distribution, the probability density function is given by:

\[ f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(x – \mu)^2}{2 \sigma^2}} \]

Using the cumulative distribution function (CDF), we can calculate percentiles by finding the point at which the desired proportion of the distribution falls to the left.

Calculating Percentile Cutoffs in R

In R, the qnorm function allows us to determine the value at any specified percentile within a normal distribution. This value, often referred to as the percentile cutoff, tells us the threshold below which a certain percentage of data falls. Let’s calculate the 90th percentile cutoff for a normal distribution with a mean of 100 and a standard deviation of 15:

# Define parameters
mean_value <- 100   # Mean of the distribution
sd_value <- 15      # Standard deviation of the distribution
percentile <- 0.90  # Desired percentile (90th percentile)

# Calculate the cutoff value
cutoff <- qnorm(percentile, mean = mean_value, sd = sd_value)
cutoff

[1] 119.2233

Using these parameters, the qnorm function calculates the value at which 90% of the data falls below. For a mean of 100 and a standard deviation of 15, this 90th percentile cutoff is approximately 119.22. This means that 90% of observations in this distribution are expected to fall below 119.22.

Understanding the Formula

The calculation of the percentile cutoff relies on the following quantile function:

\[ X = \mu + Z \times \sigma \]

where:

• \( X \) is the percentile cutoff value we’re calculating,
• \( \mu \) is the mean of the distribution,
• \( Z \) is the z-score corresponding to the specified percentile, and
• \( \sigma \) is the standard deviation.

In our example, the 90th percentile cutoff is calculated by finding the z-score for 0.90 (about 1.28) and applying it to the formula. The qnorm function does this calculation directly by translating the percentile input into the corresponding z-score and scaling it by the specified mean and standard deviation.

Practical Use Cases

Percentile cutoffs have many practical applications, including:

• Quality Control: In manufacturing, setting a cutoff at the 90th or 95th percentile can help identify outliers or items requiring additional inspection if they fall outside this threshold.
• Finance: In finance, percentiles can be used to calculate Value at Risk (VaR), where the cutoff represents the value below which a certain percentage of potential losses will occur.
• Health and Medicine: In health statistics, percentiles are used to define thresholds like BMI or blood pressure categories, where values above a certain percentile might indicate elevated risk.

Percentile cutoffs offer a powerful way to quantify relative position within a distribution, allowing for informed decision-making based on where data points fall within the expected range.

Real-Life Use Cases for Percentiles

Percentile cutoffs have various real-world applications across industries:

• Quality Control: In manufacturing, the 95th percentile can set a threshold for product dimensions, ensuring only a small percentage fall outside specifications.
• Finance: The 99th percentile in financial risk management can define extreme market movements for stress testing.
• Healthcare: Percentiles are used to compare patient test results against normal ranges. The 5th and 95th percentiles can indicate if values are significantly low or high.
• Education: Percentile scores in tests are used to rank students. For example, a 90th percentile score might indicate that a student scored higher than 90% of peers.

Visualizing the Percentile Cutoff

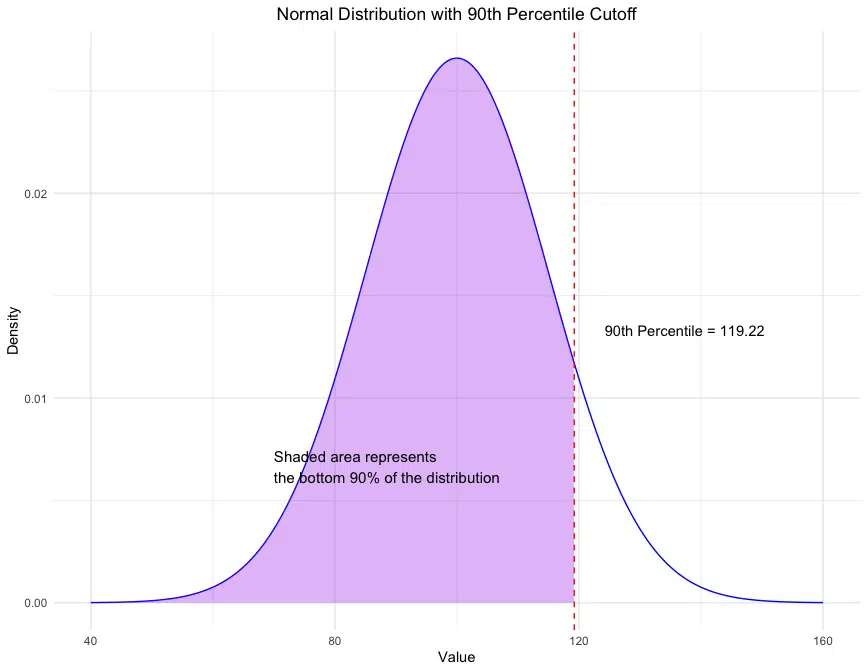
Visualizing the cutoff helps illustrate its position within the distribution. Below, we plot a normal distribution and highlight the area below the 90th percentile cutoff using R and ggplot2:

# Load ggplot2 for plotting
library(ggplot2)

# Define parameters
mean_value <- 100   # Mean of the distribution
sd_value <- 15      # Standard deviation of the distribution
percentile <- 0.90  # Desired percentile (90th percentile)

# Calculate the cutoff value
cutoff <- qnorm(percentile, mean = mean_value, sd = sd_value)

# Generate data for normal distribution
x <- seq(mean_value - 4 * sd_value, mean_value + 4 * sd_value, length = 1000)
y <- dnorm(x, mean = mean_value, sd = sd_value)
data <- data.frame(x = x, y = y)

# Plot the distribution and highlight the cutoff
ggplot(data, aes(x = x, y = y)) +
  geom_line(color = "blue") +

  # Shade area representing data below the 90th percentile cutoff
  geom_area(data = subset(data, x <= cutoff), fill = "purple", alpha = 0.3) +

  # Add a vertical line at the cutoff value
  geom_vline(xintercept = cutoff, color = "red", linetype = "dashed") +

  # Labels and title
  labs(title = "Normal Distribution with 90th Percentile Cutoff",
       x = "Value",
       y = "Density") +

  # Annotate the shaded area with text
  annotate("text", x = mean_value - 2 * sd_value, y = max(y)/4,
           label = "Shaded area represents\nthe bottom 90% of the distribution",
           color = "black", size = 4, hjust = 0) +

  # Annotate the cutoff value
  annotate("text", x = cutoff + 5, y = max(y)/2,
           label = paste("90th Percentile =", round(cutoff, 2)),
           color = "black", hjust = 0) +

  # Theme adjustments
  theme_minimal() +
  theme(plot.title = element_text(hjust = 0.5),
        plot.subtitle = element_text(hjust = 0.5))

This plot highlights the portion of the normal distribution that falls below the 90th percentile cutoff, illustrating the area where 90% of data points are expected to lie. The dashed vertical line marks the cutoff value, and the shaded purple region represents the cumulative proportion up to the 90th percentile.

Example Calculations

Here are a few common percentile calculations using the same distribution parameters:

• 50th Percentile (Median):

  qnorm(0.50, mean = mean_value, sd = sd_value)

• 95th Percentile:

  qnorm(0.95, mean = mean_value, sd = sd_value)

• 99th Percentile:

  qnorm(0.99, mean = mean_value, sd = sd_value)

These calculations provide threshold values at each specified percentile within the distribution, allowing for further statistical analysis or decision-making.

Assumptions and Limitations

Using percentiles in a normal distribution has certain assumptions and limitations:

• Assumption of Normality: These calculations assume that the data follows a normal distribution. If the data is skewed, using non-parametric percentile methods or transforming the data may be better suited.
• Sample Size: Small sample sizes may not accurately reflect the overall distribution, making percentile calculations less reliable.
• Outliers: Extreme outliers can distort the distribution, particularly when calculating high percentiles. Outlier analysis or robust statistical methods can help address this issue.

Conclusion

Calculating percentile cutoffs in R using the qnorm function is straightforward and provides valuable insights into data distribution. These cutoffs have practical applications across numerous fields, from finance to healthcare, allowing analysts to set thresholds and make data-driven decisions based on the distribution of values. By understanding and applying percentile cutoffs, we can gain a deeper understanding of variability within a dataset and make more informed decisions.

With this guide, you can calculate and interpret percentile cutoffs for normal distributions in your own data, helping you analyze and interpret patterns in diverse contexts.

Try the Percentile Cutoff for Normal Distribution Calculator

To calculate the percentile cutoff for your data, check out our Percentile Cutoff for Normal Distribution Calculator on the Research Scientist Pod.

Have fun and happy researching!