Fisher’s Exact Test in R: Independence Test for a Small Sample

Introduction

Fisher’s exact test is a statistical significance test used to determine if there are nonrandom associations between two categorical variables. Unlike the chi-square test of independence, which may not perform well with small samples or low expected frequencies, Fisher’s exact test is designed to provide precise p-values without relying on large-sample approximations, making it more reliable when expected frequencies fall below 5. It’s widely used in genetics, epidemiology, and clinical trials, where sample sizes are often limited.

Theoretical Foundation

The Hypergeometric Distribution

Fisher’s exact test is based on the hypergeometric distribution, which models the probability of obtaining specific combinations in a contingency table while keeping the marginal totals fixed. It’s called an “exact” test because it calculates the exact probability of observing the given data configuration under the null hypothesis rather than relying on approximations.

The probability of observing a particular table configuration is given by:

# Probability of a specific table configuration
p = (choose(R1, a) * choose(R2, c)) / choose(n, m)

# Where:
# R1, R2 = row totals
# a, c = cell values
# n = total sample size
# m = column total

Hypotheses

In Fisher’s exact test, we test:

• H₀ (Null hypothesis): There is no association between the two categorical variables (they are independent).
• H₁ (Alternative hypothesis): There is an association between the two categorical variables (they are dependent).

This means that under the null hypothesis, the proportion of outcomes within each category of the treatment variable should be the same, suggesting no effect of treatment on response.

One-sided vs. Two-sided Tests

Fisher’s exact test can be performed as either:

• Two-sided test: Tests for any association between variables
• One-sided test: Tests for association in a specific direction

The choice depends on your research question and prior hypotheses.

When to Use Fisher’s Exact Test

Decision Flowchart

Use this guide to decide between Fisher’s exact test and the chi-square test:

1. Total sample size < 20: Use Fisher’s exact test
2. Sample size 20-40 with any expected frequencies < 5: Use Fisher’s exact test
3. Sample size > 40:
   • All expected frequencies ≥ 5: Either test is appropriate
   • Any expected frequency < 5: Use Fisher’s exact test

Practical Example: Clinical Trial Analysis

Let’s examine a dataset from a clinical trial comparing two treatments. We’ll use R for our analysis.

Data Setup

In this clinical trial, two treatments (Drug A and Drug B) were administered to different groups of patients. Each patient’s response to treatment was recorded as either “Success” or “Failure.”

# Set random seed for reproducibility
set.seed(123)

# Create the dataset
treatment_data <- data.frame(
    Treatment = c(rep("Drug A", 12), rep("Drug B", 12)),
    Response = c("Success", "Success", "Success", "Success", "Success", "Failure",
                "Failure", "Failure", "Failure", "Failure", "Failure", "Failure",
                "Success", "Success", "Success", "Success", "Success", "Success",
                "Success", "Success", "Failure", "Failure", "Failure", "Failure")
)

# Create a robust analysis function
analyze_fisher_test <- function(data, treatment_col, response_col, conf.level = 0.95) {
    # Input validation
    if(!all(c(treatment_col, response_col) %in% names(data))) {
        stop("Specified columns not found in data")
    }
    
    # Create contingency table
    cont_table <- table(data[[treatment_col]], data[[response_col]])
    
    # Calculate expected frequencies
    expected <- chisq.test(cont_table)$expected
    
    # Perform Fisher's exact test
    fisher_result <- fisher.test(cont_table, conf.level = conf.level)
    
    return(list(
        contingency_table = cont_table,
        expected_frequencies = expected,
        test_result = fisher_result
    ))
}

# Perform analysis
results <- analyze_fisher_test(treatment_data, "Treatment", "Response")

In this section, we prepared the data for our Fisher’s exact test and built a robust analysis function. Let’s break down some important components of this code:

Setting the Random Seed for Reproducibility

# Set random seed for reproducibility
set.seed(123)

Using set.seed(123) ensures that any random operations within our R code will produce the same results each time the code is run. Setting a seed value makes the dataset generation predictable, which is essential for reproducibility. This is especially valuable in clinical or statistical analysis, where consistent results are needed for peer review or repeated studies.

Creating the Dataset

We simulate a clinical trial dataset to compare two treatments, “Drug A” and “Drug B,” and their outcomes as either “Success” or “Failure.” By defining the dataset manually, we have complete control over its structure, allowing us to illustrate Fisher’s exact test with specific values in mind:

treatment_data <- data.frame(
    Treatment = c(rep("Drug A", 12), rep("Drug B", 12)),
    Response = c("Success", "Success", "Success", "Success", "Success", "Failure",
                 "Failure", "Failure", "Failure", "Failure", "Failure", "Failure",
                 "Success", "Success", "Success", "Success", "Success", "Success",
                 "Success", "Success", "Failure", "Failure", "Failure", "Failure")
)

Building the Analysis Function

The analyze_fisher_test function encapsulates the steps needed to run Fisher’s exact test. This modular approach allows us to easily repeat the analysis on other datasets by passing different variables. The function includes:

• Input Validation: Checks that the specified treatment and response columns exist in the dataset.
• Contingency Table Creation: Generates a table of observed frequencies between treatment types and responses.
• Expected Frequency Calculation: Although Fisher’s exact test doesn’t rely on expected frequencies, calculating them can give insight into our expected distribution under the null hypothesis.
• Fisher’s Exact Test Execution: Runs Fisher’s exact test on the contingency table and returns the result.

Performing the Analysis

Finally, we call our analyze_fisher_test function outputs the contingency table, expected frequencies, and Fisher’s exact test results. This approach ensures a smooth, reusable process for conducting Fisher’s exact test on any dataset with a similar structure:

# Perform analysis
results <- analyze_fisher_test(treatment_data, "Treatment", "Response")

With the data structured and the function in place, we’re ready to interpret the test’s output to assess the association between treatment type and response outcome. This setup allows for easy adjustments if new data becomes available or we want to examine additional treatment variables.

Observed Frequencies

To better understand the observed frequencies, we can format the table using knitr :

This table suggests that there might be a slight difference in response rates between the two drugs, but Fisher’s exact test will help determine if this difference is statistically significant.

# Display the contingency table with better formatting
install.packages('knitr') # install knitr if not already installed
library(knitr)
kable(results$contingency_table)

|       | Failure| Success|
|:------|-------:|-------:|
|Drug A |       7|       5|
|Drug B |       4|       8|

This table suggests that there might be a slight difference in response rates between the two drugs, but Fisher’s exact test will help determine if this difference is statistically significant.

Expected Frequencies

Calculating expected frequencies can be helpful for visual comparisons and for understanding the distribution under the null hypothesis, even though Fisher’s exact test does not rely on them.

print(round(results$expected_frequencies, 2))

Expected frequencies under the null hypothesis:

   Failure Success
  Drug A     5.5     6.5
  Drug B     5.5     6.5

The expected frequencies show the distribution if there were no true association between treatment and response outcome.

Fisher’s Exact Test in R

To test our hypothesis, we use Fisher’s exact test:

# Perform Fisher's exact test
print(results$test_result)

Results:

	Fisher's Exact Test for Count Data

data:  contingency_table
p-value = 0.4136
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
  0.4098304 20.2574967
sample estimates:
odds ratio 
   2.67751 

In this case:

• p-value: The p-value of 0.4136 indicates that we do not have enough evidence to reject the null hypothesis at the standard 5% significance level.
• Odds ratio: The estimated odds ratio of 2.6775 suggests that the odds of a “Success” response may be higher with Drug B compared to Drug A. However, the wide confidence interval (0.4098 to 20.2575) indicates significant uncertainty due to the small sample size.

Interpretation of Results

With a p-value of 0.4136 (> 0.05), we fail to reject the null hypothesis, suggesting insufficient evidence to conclude an association between treatment type and response outcome. This wide confidence interval for the odds ratio further emphasizes the uncertainty in our estimate, reflecting the small sample size and variability in the data.

Although the odds ratio suggests a potential trend, the wide confidence interval and non-significant p-value highlight that this trend is not statistically significant, and caution is needed in interpreting any practical significance.

Combination of Plot and Statistical Test

A visual representation can help understand the association between treatment and response outcome. Here, we create a mosaic plot to illustrate the distribution visually. Mosaic plots are especially useful in categorical data analysis, allowing quick visual insight into the proportions and possible associations between variables. Variations in height between the bars signal differences in proportions, which can help visualize potential associations.”

# Create mosaic plot
install.packages('ggmosaic')
library(ggplot2)
library(ggmosaic)

ggplot(treatment_data) +
  geom_mosaic(aes(x = product(Treatment), fill = Response)) +
  labs(title = "Treatment Response by Drug Type",
       subtitle = paste("Fisher's Exact Test p-value =", 
                       round(fisher_test$p.value, 4))) +
  theme_minimal()

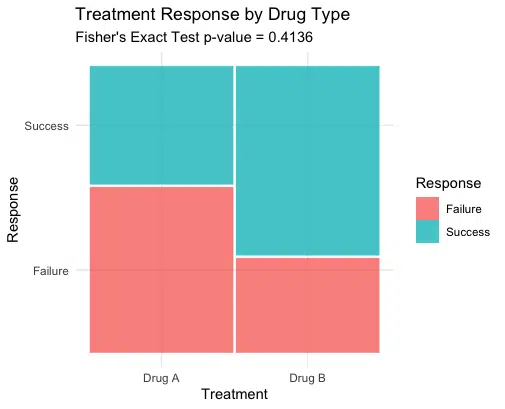
The mosaic plot visually summarises the relationship between treatment and response outcome. Differences in bar height can visually highlight proportions within each treatment group, aiding in interpreting test results.

Alternative Approaches

Chi-square Test Comparison

# Compare with chi-square test
chisq_result <- chisq.test(results$contingency_table)
print(paste("Chi-square p-value:", round(chisq_result$p.value, 4)))
print(paste("Fisher's exact p-value:", round(results$test_result$p.value, 4)))

Barnard’s Exact Test

Barnard’s test can be more powerful than Fisher’s exact test but is computationally intensive:

# Example using the Barnard package
# install.packages("Barnard")
library(Barnard)
barnard_test <- barnard.test(results$contingency_table)

Considerations and Common Pitfalls

1. Fisher’s exact test is designed for small samples and provides exact p-values without requiring large-sample approximations.
2. It avoids assumptions of the chi-square test, which requires large samples and expected frequencies > 5.
3. Insightful visualization: Mosaic plots or bar charts can visually aid the interpretation of categorical associations.
4. Interpret results cautiously: A non-significant result does not confirm independence but lacks sufficient evidence to conclude dependence.
5. Multiple Testing: When performing multiple Fisher’s exact tests, consider adjusting p-values using Bonferroni or False Discovery Rate (FDR) methods.
6. Sample Size Planning: Use power analysis to determine appropriate sample sizes for future studies.

Conclusion

Fisher’s exact test is a powerful tool for analyzing categorical data, particularly with small sample sizes. Its exact calculation of p-values makes it more reliable than chi-square tests in many situations. However, understanding its assumptions, limitations, and alternatives is crucial for practical application.

If you want to explore further, try our Fisher’s exact test calculator!

Have fun and happy researching!