How to Calculate Jaccard Similarity in R

The Jaccard similarity compares two sets of data to determine how similar they are. The value of the Jaccard similarity can be between 0 and 1, where the close the number is to 1 the more similar the two sets of data are.

This tutorial will go through how to calculate the Jaccard similarity using R with code examples.

---

Jaccard Similarity Formula

The Jaccard Similarity is a term coined by Paul Jaccard, defined as the size of the intersection divided by the size of the union of two sets. In simple terms, we can determine the Jaccard Similarity as the number of objects the two sets have in common divided by the total number of objects. If two datasets share the same members, the Similarity term will be 1. Conversely, if the two sets have no members in common, then the term will be 0.

Jaccard Similarity in R

We can define a similarity function which takes two vectors as input.

jacc <- function(x, y) {
    intersection = length(intersect(x, y))
    union = length(x) + length(y) - intersection
    return (intersection/union)
}

The Jaccard Similarity (J) is (the count of common elements in both sets) / ( the count of elements of the first set plus the count of elements in the second set minus the common elements in both sets)

Jaccard Similarity in R For Numeric Sets

Consider an example with two numeric vectors. We will call the user-defined function as follows:

x <- c(2, 3, 5, 6, 7, 11, 19, 21, 7, 4)
y <- c(19, 11, 4, 8, 22, 1, 3, 10, 17, 21)

jacc(x,y)

[1] 0.3333333

Jaccard Similarity in R For Character Vectors

We can also use the function for sets containing strings. Consider an example of two character vectors. We will call the user-defined function as follows:

x <- c('london', 'paris', 'tokyo', 'berlin', 'accra')
y <- c('accra', 'cairo', 'geneva', 'tokyo', 'lusaka')

jacc(x, y)

[1] 0.25

The Jaccard Distance

The Jaccard distance measures the dissimilarity between sets, is complementary to the Jaccard Similarity, and is obtained by subtracting the Jaccard coefficient from 1, or equivalently by dividing the difference of the size of the union and the intersection of two sets by the size of the union:

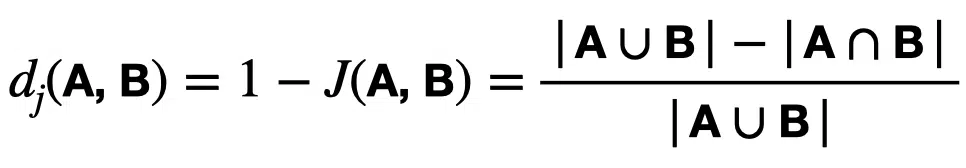
The distance is a metric on the collection of all finite sets. We can use the distance to calculate an n $latex \times$ n matrix for clustering and multidimensional scaling of n sample sets.

Jaccard Distance In R for Numeric Vectors

We can use the previously defined function to determine the Jaccard distance between two numeric sets, which is 1 – Jaccard similarity. Consider the following example with two numeric vectors:

x <- c(2, 3, 5, 6, 7, 11, 19, 21, 7, 4)
y <- c(19, 11, 4, 8, 22, 1, 3, 10, 17, 21)

jaccard_distance <- 1 - jacc(x,y)

jaccard_distance

[1] 0.6666667

Jaccard Distance In R for Character Vectors

We can use the previously defined function to determine the Jaccard distance between two character sets, which is 1 – Jaccard similarity. Consider the following example with two character vectors:

x <- c('london', 'paris', 'tokyo', 'berlin', 'accra')
y <- c('accra', 'cairo', 'geneva', 'tokyo', 'lusaka')

jaccard_distance <- 1 - jacc(x, y)
jaccard_distance

[1] 0.75

Jaccard Similarity Matrix in R

We can calculate a Jaccard similarity matrix using the vegdist() function from the vegan package. Consider the following example of a data frame consisting of two numeric vectors, we will pass the data frame to the vegdist() method and set the method to “jaccard“.

install.packages("vegan")

library(vegan)

x <- c(2, 3, 5, 6, 7, 11, 19, 21, 7, 4)

y <- c(19, 11, 4, 8, 22, 1, 3, 10, 17, 21)

df <- data.frame(x, y)

vegdist(df, method="jaccard")

Let’s run the code to see the result:

          1         2         3         4         5         6         7         8         9
2  0.4090909                                                                                
3  0.7500000 0.5625000                                                                      
4  0.6000000 0.3529412 0.3571429                                                            
5  0.2758621 0.5172414 0.6896552 0.5172414                                                  
6  0.9000000 0.8181818 0.6000000 0.6315789 0.7575758                                        
7  0.8684211 0.8000000 0.6521739 0.6666667 0.7560976 0.4545455                              
8  0.7000000 0.5937500 0.7096774 0.5483871 0.6046512 0.6129032 0.2903226                    
9  0.2692308 0.4166667 0.6250000 0.4166667 0.1724138 0.7142857 0.7222222 0.5526316          
10 0.1600000 0.4400000 0.6923077 0.5555556 0.1379310 0.8437500 0.8250000 0.6666667 0.2500000

Summary

Congratulations on reading to the end of this tutorial. Jaccard Similarity provides a simple and intuitive method of finding the similarity between objects.

For further reading on how to calculate the Jaccard similarity in Python, go to the article:

• Jaccard Similarity

Have fun and happy researching!