How to do Matrix Multiplication in R

To perform element-by-element multiplication between two matrices X and Y, you must use the * operator as follows:

X * Y

If you want to perform matrix multiplication between two matrices X and Y, you must use the %*% operator as follows:

X * Y

This tutorial will go through how to multiply matrices in R using * and %*% with the help of code examples.

---

Element by Element Multiplication Using *

Consider the following two matrices. Both matrices have two rows and two columns.

x = matrix(c(2,4,6,8), ncol=2, nrow=2)
y = matrix(c(3,6,9,12), ncol=2, nrow=2)

x 

y

   [,1] [,2]
[1,]    2    6
[2,]    4    8

   [,1] [,2]
[1,]    3    9
[2,]    6   12

The numbers in square brackets indicate the row and column numbers. If the number is before the comma, it is the row number. If the number is after the column number.

Using the * operator performs element by element multiplication between two matrices. Let’s look at the code:

prod <- x * y

prod

Let’s run the code to see the result:

 [,1] [,2]
[1,]    6   54
[2,]   24   96

We can break down the element-by-element calculations as follows:

• [1, 1] : 2 * 3 = 6
• [1, 2] : 6 * 9 = 54
• [2, 1] : 4 * 6 = 24
• [2, 2] : 8 * 12 = 96

Matrix Multiplication using %*%

We can perform matrix multiplication between two matrices using the %*% operator. Let’s look at the code.

x = matrix(c(2,4,6,8), ncol=2, nrow=2)
y = matrix(c(3,6,9,12), ncol=2, nrow=2)

prod <- x %*% y

prod

Let’s run the code to get the result:

     [,1] [,2]
[1,]   42   90
[2,]   60  132

We can break down the exact calculation as follows:

• Position [1, 1] : 2 * 3 + 6 * 6 = 42
• Position [1, 2] : 2 * 9 + 6 * 12 = 90
• Position [2, 1] : 4 * 3 + 8 * 6 = 60
• Position [2, 2] : 4 * 9 + 8 * 12 = 132

Matrix Multiplication Explained

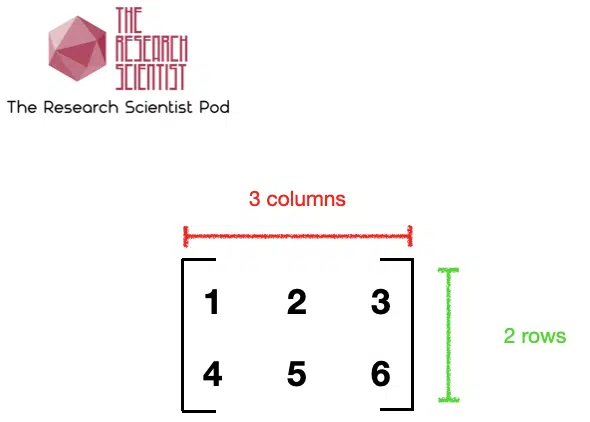
A matrix is a rectangular arrangement of numbers into rows and columns, and we refer to each number as a matrix element or entry in a matrix.

For example, the matrix below has two rows and three columns. The element in the second row in the first column of the matrix is 4.

The number of columns in the first matrix must equal the number of rows in the second matrix to perform matrix multiplication. The resultant matrix will have the number of rows of the first and the number of columns of the second matrix. Below is an example of matrix multiplication.

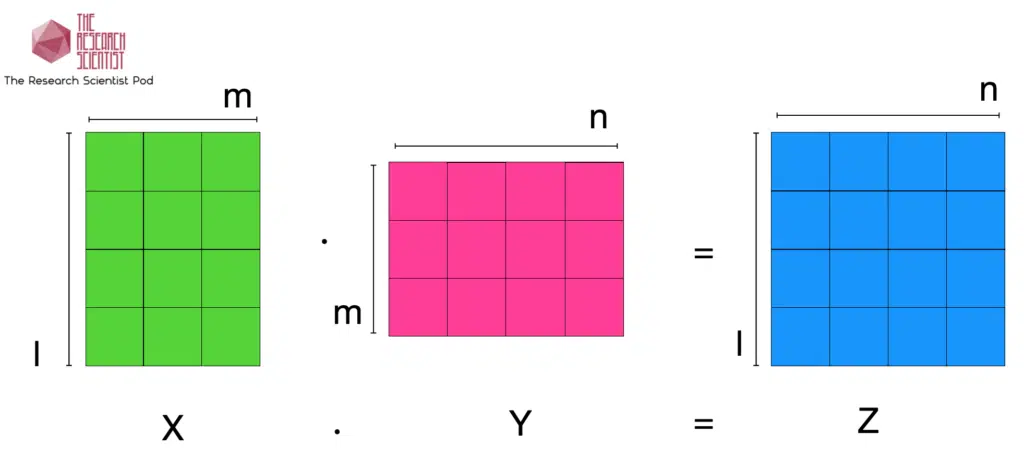
Let’s look at matrix multiplication between a 2×3 and a 3×2 matrix. The result will be a 2×2 matrix, and the green highlight shows how we perform a row by column multiplication.

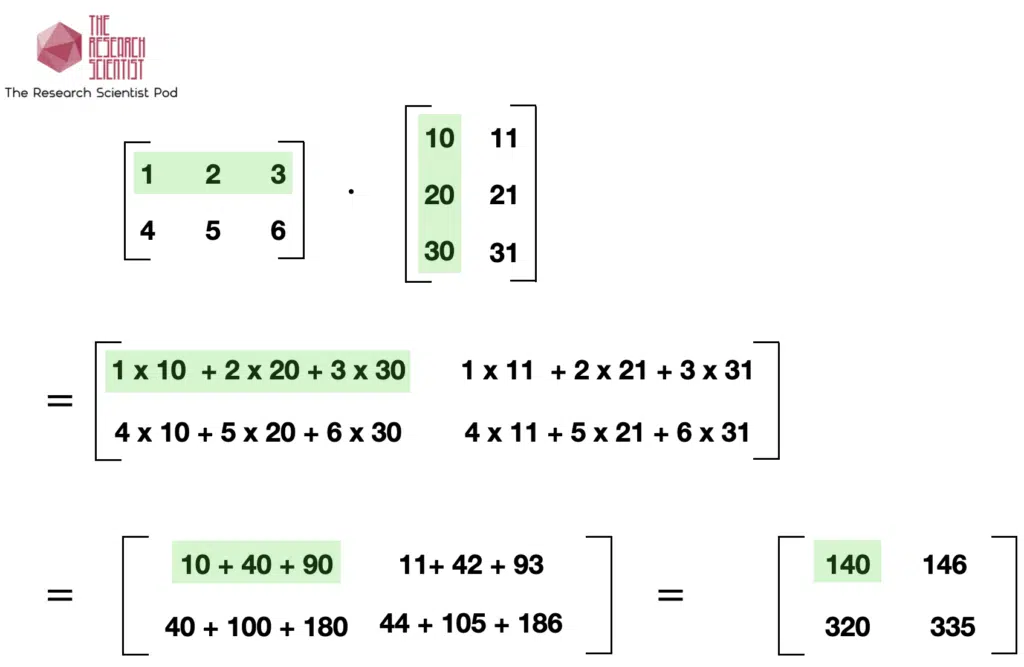
Summary

Congratulation on reading to the end of this tutorial! For further reading on how to multiply matrices in other programming languages, go to the articles:

• How to Multiply Two Matrices in Python

For further reading on matrix multiplication in R, go to the article:

• How to Solve R Error: Multiplication requires numeric/complex matrix/vector arguments

Go to the online courses page on R to learn more about coding in R for data science and machine learning.

Have fun and happy researching!