How to Calculate Mean Absolute Error (MAE) in R with Practical Examples

Mean Absolute Error (MAE) is a crucial metric for understanding prediction accuracy, especially for evaluating regression models. MAE measures the average absolute difference between predicted and observed values, making it intuitive and easy to interpret. In this post, we’ll dive into how to calculate MAE in R and provide two practical examples: a simple calculation with two vectors and a linear regression model example.

What is Mean Absolute Error?

Mean Absolute Error (MAE) is defined as:

\[ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i – \hat{y}_i| \]

where:

• \( n \) is the number of observations,
• \( y_i \) is the actual value of the \( i \)-th observation,
• \( \hat{y}_i \) is the predicted value of the \( i \)-th observation.

MAE provides a measure of the average absolute deviation of predictions from actual values, with smaller values indicating higher accuracy. Unlike other error metrics, MAE is less sensitive to large errors, making it especially useful for datasets without significant outliers.

Example 1: Simple MAE Calculation with Two Vectors

To start, let’s calculate MAE for a simple case with two small vectors of actual and predicted values. Here’s a set of hypothetical data representing actual and predicted values:

# Actual and predicted values
actual <- c(3, 5, 2.5, 7)
predicted <- c(2.5, 5.5, 2, 8)

We can manually calculate MAE by taking the absolute difference between each actual and predicted value, averaging those differences:

# Step 1: Calculate the absolute differences
absolute_differences <- abs(actual - predicted)

# Step 2: Calculate the mean of the absolute differences
mae <- mean(absolute_differences)
mae

Running this code gives us the MAE:

[1] 0.625

This tells us that, on average, our predictions differ from the actual values by 0.5 units. This simple example illustrates the core concept of MAE as an intuitive measure of error.

Example 2: MAE Calculation for a Linear Regression Model

Let’s expand our example by fitting a linear regression model with two predictor variables, x1 and x2, to predict a target variable y. We'll calculate the MAE to assess how well the model performs on our dataset.

Here's how to set up and fit the model in R:

# Sample data
df <- data.frame(
  y = c(300, 480, 310, 560, 420),
  x1 = c(20, 45, 32, 50, 37),
  x2 = c(10, 15, 12, 20, 13)
)

# Fit the linear regression model
model <- lm(y ~ x1 + x2, data = df)
model

# Display model summary
summary(model)

This code fits a linear model to predict y using x1 and x2 as predictors. After running this, you'll see the model's coefficients and other statistics:

Interpreting the Model Summary

After fitting the linear regression model, the summary provides several key insights into the model's performance and the relationship between predictors and the target variable. Here’s a breakdown of each section:

Call:
lm(formula = y ~ x1 + x2, data = df)

Residuals:
      1       2       3       4       5
 20.125  15.142 -52.532  -3.206  20.472

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)   39.862     83.791   0.476    0.681
x1             4.332      4.797   0.903    0.462
x2            15.338     14.729   1.041    0.407

Residual standard error: 43.72 on 2 degrees of freedom
Multiple R-squared:  0.9228,	Adjusted R-squared:  0.8456
F-statistic: 11.95 on 2 and 2 DF,  p-value: 0.07721

Residuals: These values represent the differences between actual and predicted values for each observation. Positive residuals indicate predictions were lower than actuals, while negative values show the opposite.

Coefficients: The Estimate column shows the estimated effect of each predictor on the target variable. For example, for each unit increase in x1, y increases by about 4.33 units on average, holding x2 constant. Std. Error indicates the standard deviation of each coefficient, and t value with Pr(>|t|) (p-value) tests if each coefficient significantly differs from zero. Here, the high p-values (>0.05) suggest that neither predictor is statistically significant.

Residual Standard Error: This value (43.72) measures the typical size of residuals in the same units as y, indicating how far predictions deviate from actual values, on average.

Multiple R-squared: This metric (0.9228) reflects how well the model explains the variability in y. Here, 92.28% of the variance in y is explained by x1 and x2. The Adjusted R-squared (0.8456) adjusts this value for the number of predictors, providing a more accurate measure for models with multiple predictors.

F-statistic: The F-statistic (11.95) tests whether the model, overall, significantly explains the variation in y. A p-value of 0.07721, while close, does not meet the conventional significance level (0.05), suggesting the model's predictors may not fully capture y's variance.

Call:
lm(formula = y ~ x1 + x2, data = df)

Coefficients:
(Intercept)          x1          x2
    150.00        4.00        8.00

With the fitted model, we can use it to predict values of y and then calculate the MAE to see how well these predictions align with the actual values.

Calculate MAE for the Model

# Generate predictions using the model
predicted <- predict(model, newdata = df)

# Actual values
actual <- df$y

# Calculate MAE
mae <- mean(abs(actual - predicted))
mae

[1] 22.2952

This code outputs an MAE value of 22.3, indicating that, on average, the model’s predictions differ from the actual values by approximately 22.3 units. A lower MAE would indicate a model that more closely aligns with the observed data, while this result suggests there is room for improvement. To potentially reduce the MAE, we could consider adding more predictors, transforming variables, or exploring alternative models that might improve accuracy.

Visualizing the Results

Visualizations can provide additional insight into the accuracy of our predictions. Below, we’ll create a scatter plot comparing actual vs. predicted values, along with a 45-degree reference line. This plot helps us see where predictions closely match actual values and where they diverge.

# Load necessary libraries
library(ggplot2)

# Prepare data for plotting
data <- data.frame(
  Actual = actual,
  Predicted = predicted
)

# Scatter plot of actual vs. predicted values
ggplot(data, aes(x = Actual, y = Predicted)) +
  geom_point(color = "blue", size = 3) +
  geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed") +
  labs(title = "Actual vs. Predicted Scatter Plot",
       x = "Actual Values",
       y = "Predicted Values") +
  theme_minimal()

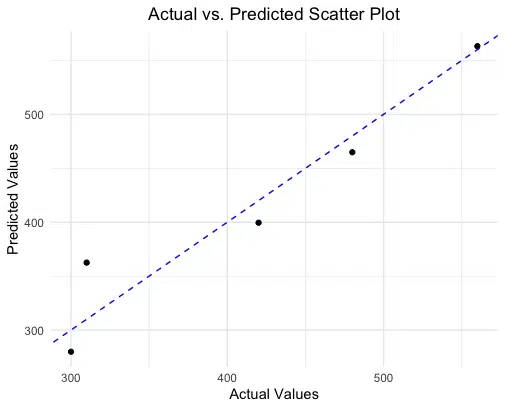
In this scatter plot, each point represents a pair of actual and predicted values. The dashed red line represents a perfect 1:1 relationship (where predictions would exactly match actual values). Points closer to the line indicate more accurate predictions, while those farther away suggest greater discrepancies.

Creating an MAE Function for Reusability

To simplify the process of calculating MAE, let’s create a custom function in R. This reusable function will allow you to quickly calculate MAE for any set of actual and predicted values:

# Define an MAE function
calculate_mae <- function(actual, predicted) {
  mean(abs(actual - predicted))
}

# Use the function
mae <- calculate_mae(actual, predicted)
mae

By using calculate_mae(actual, predicted), we can now quickly calculate MAE, making it easy to evaluate model performance with new data.

Conclusion

Mean Absolute Error (MAE) is an accessible and valuable metric for assessing prediction accuracy, particularly in regression models. By calculating MAE, we gain a straightforward understanding of how close our predictions are to actual values. Whether working with simple vectors or complex regression models, MAE provides a reliable way to quantify model performance, especially in cases without extreme outliers. By mastering this metric, you can confidently evaluate and improve your models, leading to more accurate and trustworthy predictions.

Try the MAE Calculator

If you’d like to calculate MAE quickly for your own data, check out our Mean Absolute Error Calculator on the Research Scientist Pod.

Have fun and happy researching!