How to Perform the Two-Sample t-Test (Pooled Variance) in R with Example

Introduction to the Two-Sample t-Test

The two-sample t-test (with pooled variance) is a statistical method used to determine if there is a significant difference between the means of two independent samples. It’s commonly applied when comparing groups under two different conditions or from two separate populations.

Formulae for the Two-Sample t-Test

The two-sample t-test (pooled variance) uses the following formula:

The t-value is calculated as:

\[ t = \frac{\bar{x}_1 – \bar{x}_2}{\sqrt{S_p^2 \left( \frac{1}{n_1} + \frac{1}{n_2} \right)}} \]

where:

• \(\bar{x}_1\) and \(\bar{x}_2\) are the sample means of group 1 and group 2, respectively.
• \(n_1\) and \(n_2\) are the sample sizes of group 1 and group 2, respectively.

The pooled variance \(S_p^2\) is calculated as:

\[ S_p^2 = \frac{(n_1 – 1)s_1^2 + (n_2 – 1)s_2^2}{n_1 + n_2 – 2} \]

• \(s_1^2\) and \(s_2^2\) are the variances of group 1 and group 2, respectively.

When to Use a Two-Sample t-Test

This test is suitable when:

• We have two independent samples of quantitative data.
• The variances in the two samples are assumed to be equal (homogeneity of variance).
• The data in each group is approximately normally distributed.

Performing a Two-Sample t-Test in R

In R, you can use the t.test() function to perform a two-sample t-test with equal variances by setting var.equal = TRUE. Here’s an example:

t.test(sample1, sample2, var.equal = TRUE)

Practical Example

Suppose we have two independent samples representing the test scores of two different classes:

# Test scores of two classes
class1_scores <- c(85, 78, 82, 90, 88, 76, 80, 84, 79, 81)
class2_scores <- c(75, 80, 78, 85, 77, 82, 79, 83, 76, 81)

# Perform the two-sample t-test
result <- t.test(class1_scores, class2_scores, var.equal = TRUE)
result

Interpreting Results

The output from R’s t.test() provides several values that help us understand the results:

• t-value: This is the calculated t-statistic, which indicates how far apart the two sample means are, relative to the variability in the data. A higher absolute t-value suggests a larger difference between means.
• Degrees of Freedom (df): The degrees of freedom for the test, calculated as n1 + n2 - 2 for the two-sample t-test. This value affects the critical t-value used to determine significance.
• p-value: This is the probability of observing a t-statistic as extreme as the one calculated if the null hypothesis (no difference in means) is true. A p-value below 0.05 (or your chosen significance level) suggests that the difference in means is statistically significant.
• Confidence Interval: The 95% confidence interval provides a range within which the true difference in means is likely to fall. If this interval includes 0, it suggests that the difference between group means may not be statistically significant.
• Sample Estimates: These are the means of each group, which help you see the actual average values for comparison.

Example Output Interpretation

    Two Sample t-test

    data:  class1_scores and class2_scores
    t = 1.5574, df = 18, p-value = 0.1368
    alternative hypothesis: true difference in means is not equal to 0
    95 percent confidence interval:
     -0.9422715  6.3422715
    sample estimates:
    mean of x mean of y
         82.3      79.6

Here’s how to interpret this output:

• t-value (1.5574): The t-value shows a moderate difference between the group means, but it is not strong enough to be statistically significant at the 0.05 level.
• p-value (0.1368): Since the p-value is greater than 0.05, we fail to reject the null hypothesis. This means we do not have enough evidence to conclude that there is a statistically significant difference between the two group means.
• Confidence Interval (-0.94, 6.34): The interval includes 0, which aligns with the p-value, indicating that the difference between means may not be significant. The interval suggests that the true difference in means could plausibly range from slightly negative to positive.
• Mean of Group 1 (82.3) and Mean of Group 2 (79.6): The sample means give a descriptive comparison, showing that Group 1 has a slightly higher average, though this difference is not statistically significant.

In summary, this test suggests no statistically significant difference between the means of the two classes, meaning any observed difference could be due to chance or sample variability.

Visualizing the T-Distribution and P-Value

To help interpret the results of the t-test, we can visualize the calculated t-value on a t-distribution plot. In this two-tailed test, the plot shows the probability of observing a t-value as extreme as ours (1.5574) in both tails of the distribution, representing our two-tailed p-value.

The following plot highlights the t-distribution with 18 degrees of freedom, where:

• Blue line: Represents the t-distribution curve, showing the probability density of t-values.
• Purple shaded areas: Correspond to the regions in both tails beyond our calculated t-value, representing the probability of obtaining a t-value as extreme or more extreme.
• Red dashed lines: Mark the calculated t-value (±1.5574), allowing us to see how far it is from the center of the distribution.

This visual can help clarify why, in this case, we fail to reject the null hypothesis: our t-value does not fall within the critical regions for statistical significance (e.g., beyond ±2.101 for α = 0.05 with 18 degrees of freedom).

# R code to generate the plot
library(ggplot2)

# Define parameters
df <- 18  # degrees of freedom
t_value <- 1.5574  # calculated t-value
p_value_two_tailed <- 2 * pt(abs(t_value), df = df, lower.tail = FALSE)

# Generate data
x <- seq(-4, 4, length = 1000)
y <- dt(x, df)

# Create the plot
ggplot(data.frame(x, y), aes(x, y)) +
  geom_line(color = "blue") +
  geom_area(data = subset(data.frame(x, y), x >= t_value), aes(x, y), fill = "purple", alpha = 0.5) +
  geom_area(data = subset(data.frame(x, y), x <= -t_value), aes(x, y), fill = "purple", alpha = 0.5) +
  geom_vline(xintercept = c(t_value, -t_value), color = "red", linetype = "dashed") +
  labs(title = "Two-Tailed Test: t-Score and P-Value",
       x = "t-Score",
       y = "Density") +
  annotate("text", x = 0, y = 0.2, label = paste("p-value =", round(p_value_two_tailed, 4)), color = "purple") +
  theme_minimal() +
  theme(plot.title = element_text(hjust = 0.5))

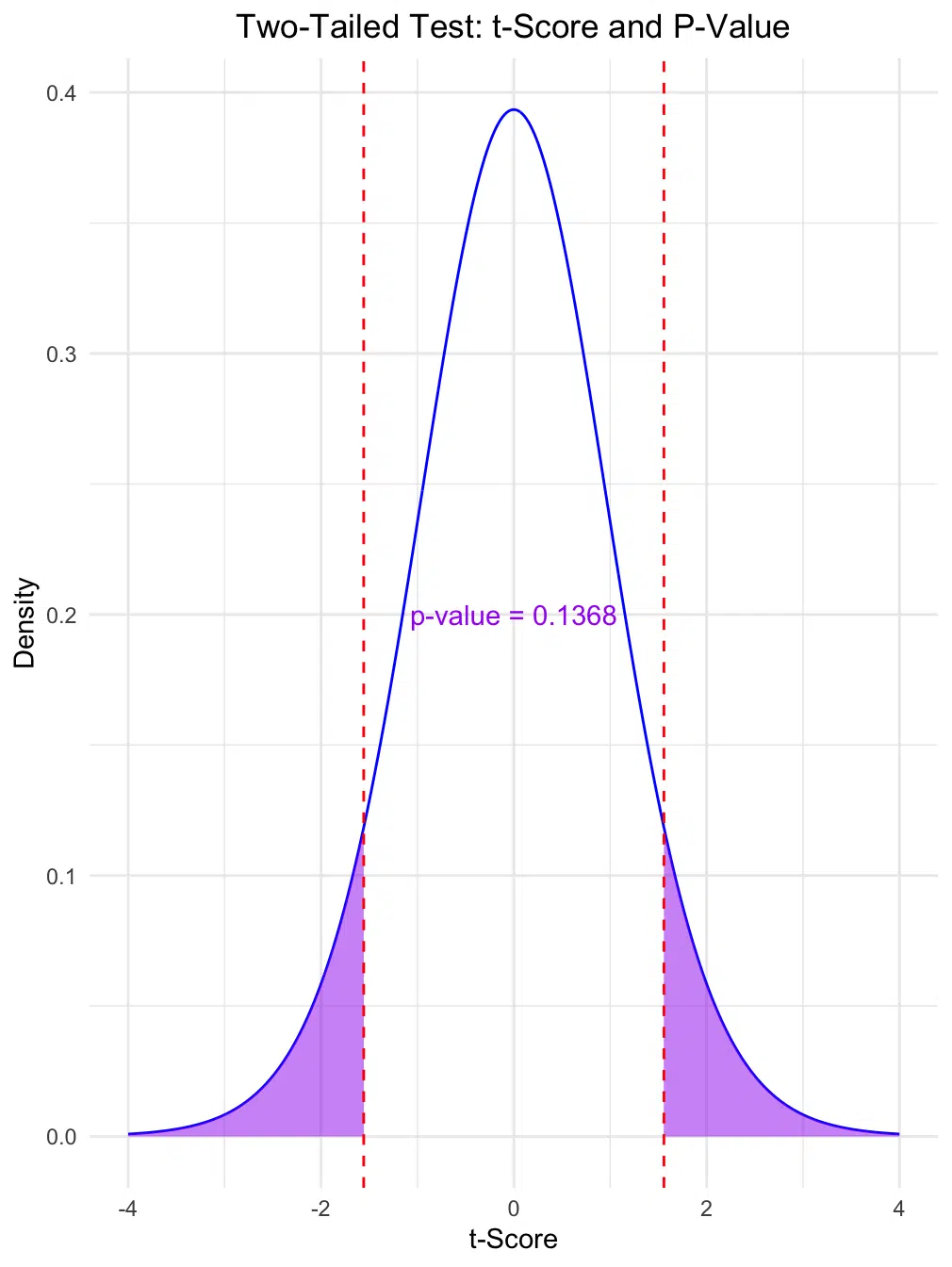
From this plot, we can visually confirm the result of our two-sample t-test: the calculated t-value does not fall within the critical regions for a significant difference. This additional visual is especially useful for interpreting results and understanding why we fail to reject the null hypothesis in this example.

Assumptions and Limitations

Assumptions

• Normality: Each group’s data should be approximately normally distributed, especially important for small samples (less than 30 observations).
• Independence: Observations in each group must be independent of each other.
• Equal Variance (Homogeneity of Variance): The two samples should have similar variances, which can be assessed with a test like Levene's test.

Limitations

• Violation of Equal Variance: When variances are not equal, using a two-sample t-test with pooled variance can lead to inaccurate results. Use Welch's t-test if variances are unequal.
• Sensitivity to Outliers: Outliers in the data can impact the mean and variance, potentially skewing results. Consider transforming data or using robust methods if outliers are present.
• Sample Size Requirements: For small sample sizes, the assumption of normality is crucial. With larger samples, the t-test is more robust to non-normality due to the central limit theorem.

Conclusion

The two-sample t-test with pooled variance is a useful tool for comparing the means of two independent samples under the assumption of equal variance. It provides a straightforward way to assess if a significant difference exists between two group means. R’s t.test() function makes it easy to implement this test and interpret the results for data-driven decision-making.

To calculate the two-sample t-test for your data, check out our Two-Sample t-Test Calculator on Research Scientist Pod.