How to Find the Factorial of a Number in Python

The factorial of a positive integer n is the multiplication operation of all integers smaller than or equal to n. The notation of the factorial is the exclamation mark, n!. For example, the factorial of 5 is:

5! = 5 * 4 * 3 * 2 * 1 = 120

This tutorial will go through how to calculate the factorial of a number in Python recursively, iteratively and using the math.factorial() function.

---

Finding the Factorial of a Number Using Recursive Function

Recursion is when a function refers to itself to solve a problem. In every function call, the problem becomes smaller until the call reaches a base case, after which it will return the result to each intermediate call until it returns the final result to the first call.

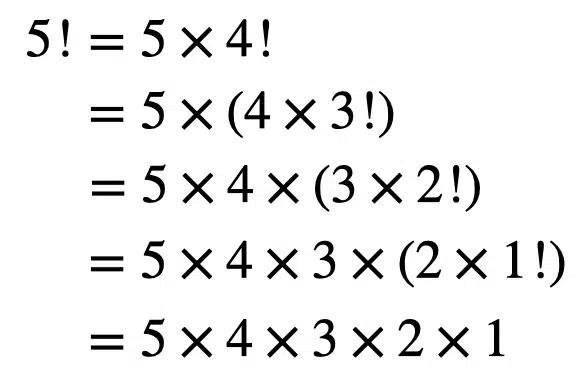
Let’s look at the example of calculating the factorial of 5. 5! breaks down to 5 * 4!. The 4! breaks down to 4 * 3!, 3! breaks down to 3 * 2! and so on. When the function reaches the base case of 1!, the function will return the result to the caller. Let’s look at how to implement the recursive solution in Python:

def factorial(n):

    if (n == 1 or n == 0):

        return 1

    else:

        return n * factorial(n-1)

In the above function, we use recursion to get the factorial of a number. The function takes the parameter n. If the number is 0 or 1, the function will return the value of 1. Otherwise, it will recursively call the factorial function with the value (n – 1) and multiply it by n.

Let’s test the recursive function with the number 5.

number = 5

print(f'Factorial of {number} is {factorial(number)}')

Factorial of 5 is 120

Finding the Factorial of a Number Using Iterative Function

def factorial(n):

    if n ≺ 0:

        print('Illegal value for calculating the factorial. The Number must be >= 0')

        return 0

    elif n == 0 or n == 1:

        return 1

    else:

        fact = 1

        while(n > 1):

            fact *= n

            n -= 1

        return fact

In the above code, we ask for a number as input. If the number is 0 or 1, the function returns 1. Otherwise, we initialize the result, fact to 1, then start a while loop where we multiply the fact by the target number. At the end of each iteration, we reduce the target number by one. The loop will end once the target number reaches 1, then the function returns the result.

Let’s run the code to get the result:

number = 5

print(f'Factorial of {number} is {factorial(number)}')

Factorial of 5 is 120

Finding the Factorial of a Number Using math.factorial()

We can use the math module, which provides the factorial() method to calculate the factorial of a number. Let’s look at an example:

import math 

def factorial(n):

    return(math.factorial(n))

In the above code, we define a function that calls the factorial function. Let’s pass a number to the function and print the factorial to the console:

number = 5

print(f'Factorial of {number} is {factorial(number)}')

Factorial of 5 is 120

Summary

Congratulations on reading to the end of this tutorial! You have gone through how to calculate the factorial of a number in Python iteratively, recursively, and with math.factorial(). The factorial concept has applications in many mathematical concepts such as permutations, probability, and series. The factorial is a function that multiplies a number by every number below it until 1. Learning how to implement the factorial is particularly helpful for understanding how recursion works in Python.

For further reading on recursive functions, go to the article: How to Write the Fibonacci Sequence in Python.

Go to the online courses page on Python to learn more about coding in Python for data science and machine learning.

Have fun and happy researching!