SST, SSR, and SSE Calculations in Python: A Comprehensive Guide

by | Python, Statistics

Introduction

Understanding how well a regression model fits data requires analyzing different components of variance. This guide shows how to implement these calculations in Python, providing both theoretical background and practical implementation.

Table of Contents

Mathematical Foundations

Total Sum of Squares (SST)

SST measures the total variation in the dependent variable (y) around its mean. It represents the total amount of variability in the data:

Formula:

\[ SST = \sum(y_i – \bar{y})^2 \]

Where:

  • \( y_i \) = each observed value
  • \( \bar{y} \) = the mean of all observed values

This value is always positive because it sums the squared differences between the observed values and their mean.

Regression Sum of Squares (SSR)

SSR quantifies the variation explained by the regression model:

Formula:

\[ SSR = \sum(\hat{y}_i – \bar{y})^2 \]

Where:

  • \( \hat{y}_i \) = each predicted value
  • \( \bar{y} \) = the mean of the observed values

A higher SSR indicates that the regression model explains a large proportion of the variability in the data.

Error Sum of Squares (SSE)

SSE measures the unexplained variation:

Formula:

\[ SSE = \sum(y_i – \hat{y}_i)^2 \]

Where:

  • \( y_i \) = each observed value
  • \( \hat{y}_i \) = each predicted value

Lower SSE indicates better model fit.

The Fundamental Relationship

\[ SST = SSR + SSE \]

This relationship shows how total variation splits between explained and unexplained components.

Coefficient of Determination (R²)

\[ R^2 = \frac{SSR}{SST} = 1 – \frac{SSE}{SST} \]

Interpretation:

  • \( R^2 = 1 \): Perfect model fit
  • \( R^2 = 0 \): Model explains no variance
  • Higher \( R^2 \) indicates better fit

Prerequisites and Setup

setup.py
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# Sample data
hours = np.array([2, 4, 6, 8, 10])
scores = np.array([65, 75, 85, 90, 95])

# Reshape for sklearn
X = hours.reshape(-1, 1)
y = scores

Python Implementation

Calculating SST (Total Sum of Squares)

Total Sum of Squares (SST) measures the overall variability of the dependent variable (y) around its mean. It captures the total deviation of the observed values from the mean of the dataset. SST is an essential component in regression analysis as it provides a baseline measure of variance that helps evaluate how well a model explains the data.

The formula for SST is:

\[ SST = \sum (y_i – \bar{y})^2 \]

Where:

  • \( y_i \) = each observed value
  • \( \bar{y} \) = the mean of all observed values

To calculate SST:

  1. Compute the mean of the dependent variable, \( \bar{y} \).
  2. For each observed value, calculate the difference between the value and the mean.
  3. Square each difference to eliminate negative values and emphasize larger deviations.
  4. Sum all the squared differences to obtain SST.

Here’s the Python implementation of SST calculation:

calculate_sst.py
def calculate_sst(y):
    """Calculate Total Sum of Squares (SST)"""
    y_mean = np.mean(y)
    sst = np.sum((y - y_mean) ** 2)

    # Print intermediate steps for better understanding
    print(f"Mean (\u0305y): {y_mean:.2f}")
    for i, yi in enumerate(y):
        diff = yi - y_mean
        print(f"Point {i+1}: ({yi:.2f} - {y_mean:.2f})² = {diff**2:.2f}")
    print(f"SST = {sst:.2f}")

    return sst

# Example Usage
y = np.array([65, 75, 85, 90, 95])  # Sample data
sst = calculate_sst(y)
Mean (ȳ): 82.00
Point 1: (65.00 – 82.00)² = 289.00
Point 2: (75.00 – 82.00)² = 49.00
Point 3: (85.00 – 82.00)² = 9.00
Point 4: (90.00 – 82.00)² = 64.00
Point 5: (95.00 – 82.00)² = 169.00
SST = 580.00

This step-by-step calculation ensures transparency and makes it easier to debug potential errors in your regression analysis.

Pro Tip: The SST value remains constant for a given dataset, regardless of the model you apply. It acts as a reference point for evaluating the model’s performance.

Calculating SSR (Regression Sum of Squares)

Regression Sum of Squares (SSR) quantifies the variation in the dependent variable (y) that is explained by the regression model. It measures how well the model’s predictions (ŷ) align with the overall trend of the data.

The formula for SSR is:

\[ SSR = \sum (\hat{y}_i – \bar{y})^2 \]

Where:

  • \( \hat{y}_i \) = each predicted value
  • \( \bar{y} \) = the mean of all observed values

To calculate SSR:

  1. Compute the mean of the observed values, \( \bar{y} \).
  2. For each predicted value, calculate the difference between the value and the mean.
  3. Square each difference to eliminate negative values and emphasize larger deviations.
  4. Sum all the squared differences to obtain SSR.

Here’s the Python implementation of SSR calculation:

calculate_ssr.py
def calculate_ssr(y, y_pred):
    """Calculate Regression Sum of Squares (SSR)"""
    y_mean = np.mean(y)
    ssr = np.sum((y_pred - y_mean) ** 2)

    # Print intermediate steps for better understanding
    print(f"Mean (\u0305y): {y_mean:.2f}")
    for i, yp in enumerate(y_pred):
        diff = yp - y_mean
        print(f"Point {i+1}: ({yp:.2f} - {y_mean:.2f})² = {diff**2:.2f}")
    print(f"SSR = {ssr:.2f}")

    return ssr

# Example Usage
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)
ssr = calculate_ssr(y, y_pred)
Mean (̅y): 82.00
Point 1: (67.00 – 82.00)² = 225.00
Point 2: (74.50 – 82.00)² = 56.25
Point 3: (82.00 – 82.00)² = 0.00
Point 4: (89.50 – 82.00)² = 56.25
Point 5: (97.00 – 82.00)² = 225.00
SSR = 562.50

By calculating SSR, we can determine how much of the variation in the data is explained by the regression model, which is critical for evaluating its performance.

Pro Tip: A higher SSR value relative to SST indicates that the model explains a significant portion of the variability in the data.

Calculating SSE (Error Sum of Squares)

Error Sum of Squares (SSE) represents the variation in the dependent variable (y) that is not explained by the regression model. It measures the discrepancy between the observed data points and the predicted values (ŷ).

The formula for SSE is:

\[ SSE = \sum (y_i – \hat{y}_i)^2 \]

Where:

  • \( y_i \) = each observed value
  • \( \hat{y}_i \) = each predicted value

To calculate SSE:

  1. For each observed value, calculate the difference between the value and the corresponding predicted value.
  2. Square each difference to eliminate negative values and emphasize larger deviations.
  3. Sum all the squared differences to obtain SSE.

Here’s the Python implementation of SSE calculation:

calculate_sse.py
def calculate_sse(y, y_pred):
    """Calculate Error Sum of Squares (SSE)"""
    sse = np.sum((y - y_pred) ** 2)

    # Print intermediate steps for better understanding
    for i, (yi, yp) in enumerate(zip(y, y_pred)):
        diff = yi - yp
        print(f"Point {i+1}: ({yi:.2f} - {yp:.2f})² = {diff**2:.2f}")
    print(f"SSE = {sse:.2f}")

    return sse

# Example Usage
y = np.array([65, 75, 85, 90, 95])  # Observed data
sse = calculate_sse(y, y_pred) # Using y_pred from model.predict(X)
Point 1: (65.00 – 67.00)² = 4.00
Point 2: (75.00 – 74.50)² = 0.25
Point 3: (85.00 – 82.00)² = 9.00
Point 4: (90.00 – 89.50)² = 0.25
Point 5: (95.00 – 97.00)² = 4.00
SSE = 17.50

By calculating SSE, we can assess the amount of error or unexplained variance in the regression model, which helps evaluate its accuracy.

Pro Tip: A lower SSE value indicates a better model fit, as it means the predictions closely align with the actual data points.

Implementation Tips:

  • Always reshape your X data for sklearn using reshape(-1, 1) for single features
  • Use NumPy’s efficient array operations for calculations
  • Verify the SST = SSR + SSE relationship to validate calculations
  • Remember to handle potential numerical precision issues in floating-point calculations

Visualization

To better understand the components of regression analysis, let’s visualize the data points, regression line, and the components SST, SSR, and SSE. We will write a Python script to plot the three subplots showing each component with the observed data, the fitted line and the mean.

visualize_regression.py
import numpy as np
import matplotlib.pyplot as plt

def plot_regression_components(X, y, y_pred):
    """Visualize regression components (SST, SSR, SSE) in separate subplots"""
    y_mean = np.mean(y)
    fig, axs = plt.subplots(3, 1, figsize=(12, 18), sharex=True)

    # Subplot 1: SSR
    axs[0].scatter(X, y, color='blue', label='Actual Data')
    axs[0].plot(X, y_pred, color='red', label='Regression Line')
    axs[0].axhline(y=y_mean, color='green', linestyle='--', label='Mean Line')
    for xi, y_pred_i in zip(X.flatten(), y_pred):
        axs[0].plot([xi, xi], [y_mean, y_pred_i], linestyle='-.', color='r', alpha=0.7)
    axs[0].set_title('Regression Sum of Squares (SSR)')
    axs[0].set_ylabel('Test Scores')
    axs[0].legend()
    axs[0].grid(alpha=0.3)

    # Subplot 2: SSE
    axs[1].scatter(X, y, color='blue', label='Actual Data')
    axs[1].plot(X, y_pred, color='red', label='Regression Line')
    for xi, (yi, y_pred_i) in zip(X.flatten(), zip(y, y_pred)):
        axs[1].plot([xi, xi], [y_pred_i, yi], linestyle='-', color='b', alpha=0.7)
    axs[1].axhline(y=y_mean, color='green', linestyle='--', label='Mean Line')
    axs[1].set_title('Error Sum of Squares (SSE)')
    axs[1].set_ylabel('Test Scores')
    axs[1].legend()
    axs[1].grid(alpha=0.3)

    # Subplot 3: SST
    axs[2].scatter(X, y, color='blue', label='Actual Data')
    axs[2].plot(X, y_pred, color='red', label='Regression Line')
    axs[2].axhline(y=y_mean, color='green', linestyle='--', label='Mean Line')
    for xi, yi in zip(X.flatten(), y):
        axs[2].plot([xi, xi], [y_mean, yi], linestyle=':', color='g', alpha=0.7)
    axs[2].set_title('Total Sum of Squares (SST)')
    axs[2].set_xlabel('Study Hours')
    axs[2].set_ylabel('Test Scores')
    axs[2].legend()
    axs[2].grid(alpha=0.3)

    plt.tight_layout()
    plt.show()

# Example Usage
X = np.array([2, 4, 6, 8, 10]).reshape(-1, 1)
y = np.array([65, 75, 85, 90, 95])
y_pred = model.predict(X)
plot_regression_components(X, y, y_pred)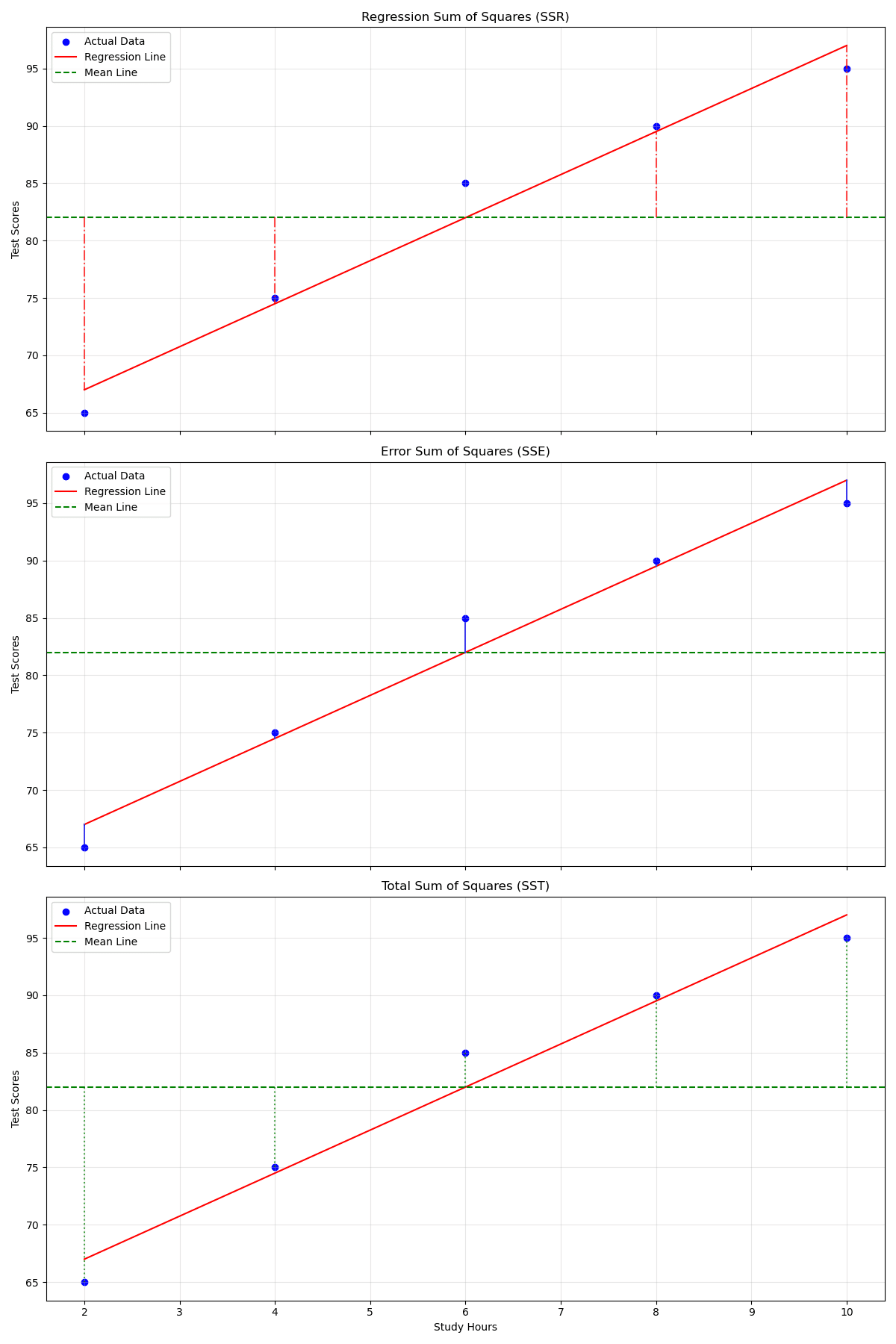
Three subplots visualizing SST, SSR, and SSE in regression analysis. The first subplot shows SSR with vertical lines connecting the predicted values to the mean of observed data, representing the explained variation. The second subplot highlights SSE with vertical lines showing residuals, or differences between observed and predicted values. The third subplot illustrates SST, showing the total variability of observed data around the mean, with vertical lines connecting observed values to the mean. The mean line is displayed consistently across all subplots, and the regression line is included in the SST and SSR plots for context.
Figure: Visualization of SST, SSR, and SSE in regression analysis, highlighting their relationships and contributions to total variability.

The updated figure consists of three subplots that highlight the relationships between SST, SSR, and SSE:

  • Regression Sum of Squares (SSR): The first subplot shows how the regression line captures the explained variation in the data. Vertical lines represent the differences between the predicted values and the mean of the observed data.
  • Error Sum of Squares (SSE): The second subplot visualizes the residuals or errors, which are the differences between the observed data and the predicted values. Vertical lines illustrate these discrepancies.
  • Total Sum of Squares (SST): The final subplot demonstrates the total variability of the observed data around the mean. The regression line is included for context, and vertical lines represent the differences between the observed values and the mean.

Together, these plots emphasize the fundamental relationship:

\[ SST = SSR + SSE \]

This equation illustrates how the total variability (SST) is partitioned into the variability explained by the model (SSR) and the unexplained variability (SSE). Observing these components separately provides insight into the regression model’s performance and fit quality.

Complete Python Implementation

This section provides the full implementation for calculating the regression components: Total Sum of Squares (SST), Regression Sum of Squares (SSR), and Error Sum of Squares (SSE). By combining these calculations with a visualization, we can thoroughly analyze the regression model’s performance and fit. The code also verifies the fundamental relationship \( SST = SSR + SSE \) and calculates the coefficient of determination \( R^2 \), which measures the proportion of variance explained by the model.

complete_analysis.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

def plot_regression_components(X, y, y_pred):
    """Visualize regression components (SST, SSR, SSE) in separate subplots"""
    y_mean = np.mean(y)
    fig, axs = plt.subplots(3, 1, figsize=(12, 18), sharex=True)

    # Subplot 1: SSR
    axs[0].scatter(X, y, color='blue', label='Actual Data')
    axs[0].plot(X, y_pred, color='red', label='Regression Line')
    axs[0].axhline(y=y_mean, color='green', linestyle='--', label='Mean Line')
    for xi, y_pred_i in zip(X.flatten(), y_pred):
        axs[0].plot([xi, xi], [y_mean, y_pred_i], linestyle='-.', color='r', alpha=0.7)
    axs[0].set_title('Regression Sum of Squares (SSR)')
    axs[0].set_ylabel('Test Scores')
    axs[0].legend()
    axs[0].grid(alpha=0.3)

    # Subplot 2: SSE
    axs[1].scatter(X, y, color='blue', label='Actual Data')
    axs[1].plot(X, y_pred, color='red', label='Regression Line')
    for xi, (yi, y_pred_i) in zip(X.flatten(), zip(y, y_pred)):
        axs[1].plot([xi, xi], [y_pred_i, yi], linestyle='-', color='b', alpha=0.7)
    axs[1].axhline(y=y_mean, color='green', linestyle='--', label='Mean Line')
    axs[1].set_title('Error Sum of Squares (SSE)')
    axs[1].set_ylabel('Test Scores')
    axs[1].legend()
    axs[1].grid(alpha=0.3)

    # Subplot 3: SST
    axs[2].scatter(X, y, color='blue', label='Actual Data')
    axs[2].plot(X, y_pred, color='red', label='Regression Line')
    axs[2].axhline(y=y_mean, color='green', linestyle='--', label='Mean Line')
    for xi, yi in zip(X.flatten(), y):
        axs[2].plot([xi, xi], [y_mean, yi], linestyle=':', color='g', alpha=0.7)
    axs[2].set_title('Total Sum of Squares (SST)')
    axs[2].set_xlabel('Study Hours')
    axs[2].set_ylabel('Test Scores')
    axs[2].legend()
    axs[2].grid(alpha=0.3)

    plt.tight_layout()
    plt.show()

# Data setup
hours = np.array([2, 4, 6, 8, 10])  # Independent variable
scores = np.array([65, 75, 85, 90, 95])  # Dependent variable
X = hours.reshape(-1, 1)
y = scores

# Fit the Linear Regression model
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)  # Predicted values

# Calculate the mean of y
y_mean = np.mean(y)

# Calculate Sum of Squares components
sst = np.sum((y - y_mean) ** 2)  # Total Sum of Squares
ssr = np.sum((y_pred - y_mean) ** 2)  # Regression Sum of Squares
sse = np.sum((y - y_pred) ** 2)  # Error Sum of Squares

# Print model parameters and summary
print(f"Model Parameters:")
print(f"Intercept (β₀): {model.intercept_:.2f}")
print(f"Slope (β₁): {model.coef_[0]:.2f}")
print(f"\nSum of Squares Components:")
print(f"SST (Total Variance): {sst:.2f}")
print(f"SSR (Explained Variance): {ssr:.2f}")
print(f"SSE (Unexplained Variance): {sse:.2f}")
print(f"R² (Coefficient of Determination): {ssr / sst:.4f}")

# Call the function to visualize components
plot_regression_components(X, y, y_pred)

Code Output:

Model Parameters:
Intercept (β₀): 59.50
Slope (β₁): 3.75

Sum of Squares Components:
SST (Total Variance): 580.00
SSR (Explained Variance): 562.50
SSE (Unexplained Variance): 17.50
R² (Coefficient of Determination): 0.9698

Summary

  • The model explains 96.98% of the variance (R² = 0.9698): This indicates that the regression model captures almost all of the variability in the dependent variable (test scores) based on the independent variable (study hours). An \(R^2\) value close to 1 suggests a strong model fit, meaning the model effectively predicts the observed data.
  • Total variance (SST) = 580.00: SST represents the total variability in the dataset, calculated as the sum of squared differences between each observed value and the mean. This provides a baseline measure of the total spread of the data points.
  • Explained variance (SSR) = 562.50: SSR quantifies the variability explained by the regression model. It shows how well the regression line accounts for the differences between the predicted values and the mean. A high SSR value relative to SST indicates a good model fit.
  • Unexplained variance (SSE) = 17.50: SSE captures the residual or unexplained variability, calculated as the sum of squared differences between the observed values and the predicted values. A low SSE value indicates minimal error, meaning the model predictions are close to the actual observations.
  • The relationship SST = SSR + SSE is verified: 580.00 = 562.50 + 17.50: This fundamental equation confirms that the total variability (SST) is partitioned into two components: the explained variability (SSR) and the unexplained variability (SSE). It validates the correctness of the calculations and ensures the model follows the principles of linear regression analysis.

These results demonstrate the effectiveness of the regression model in explaining the variance in the dataset, highlighting its predictive accuracy and low error rate. The high \(R^2\) value and low SSE together suggest that study hours are a strong predictor of test scores within this dataset.

Implementation Tips:

  • Always reshape your X data for sklearn using reshape(-1, 1) for single features: Scikit-learn requires the independent variable \(X\) to have a 2-dimensional shape, even for a single feature. Using reshape(-1, 1) transforms a 1D array into the required format where rows represent samples and columns represent features.
    • Why It’s Important: Without reshaping, sklearn’s methods (like LinearRegression) will raise an error because they expect \(X\) to be a 2D array.
    • Practical Tip: If \(X\) is already multidimensional, you can verify its shape using X.shape before applying transformations.
    • Example: A 1D array like [2, 4, 6] becomes [[2], [4], [6]] after reshaping, making it compatible with sklearn models.
  • Use NumPy’s efficient array operations to calculate variance components: NumPy provides optimized functions for numerical operations, such as summing arrays and calculating means, that are faster and less error-prone than manual loops.
    • Why NumPy: It leverages vectorized computations, reducing overhead and ensuring consistency across calculations like SST, SSR, and SSE.
    • Example: Instead of summing squared differences in a loop, use np.sum((y - y_mean) ** 2) for SST, which is both concise and efficient.
    • Best Practices: Utilize NumPy’s built-in functions, like np.mean and np.sum, to avoid potential errors and simplify your code.
  • Verify the relationship SST = SSR + SSE to ensure the correctness of your calculations: This fundamental equation splits the total variance into explained and unexplained components, serving as a checkpoint for regression analysis.
    • Why It’s Important: Ensuring this relationship holds validates that your calculations for SST, SSR, and SSE are correct and consistent.
    • Practical Tip: If the equation doesn’t balance, review intermediate steps like the computation of \(y_{mean}\), \(y_{pred}\), or the squared differences to identify discrepancies.
    • Example: For \( SST = 580.00 \), \( SSR = 562.50 \), and \( SSE = 17.50 \), the sum \( SSR + SSE \) should equal \( SST \) (580.00).
  • Address potential floating-point precision issues in larger datasets: Floating-point arithmetic can introduce small errors when working with large datasets or extreme values, such as summing very large and very small numbers (subtractive cancellation) or performing calculations that cause underflow or overflow. These errors may accumulate, affecting results like SST, SSR, SSE, and \(R^2\).
    • Mitigation Strategies:
      • Use libraries like NumPy for efficient and precise numerical computations.
      • Normalize or scale data to reduce extreme magnitudes.
      • Opt for higher precision data types (e.g., float64) when needed.
    • Importance: Precision is critical in fields like finance, science, and machine learning, where small errors can significantly impact outcomes.

Implementation with Statsmodels OLS

The statsmodels library is a powerful tool for performing regression analysis in Python. Unlike scikit-learn, which focuses on predictive modeling, statsmodels provides detailed statistical summaries, making it ideal for understanding the underlying relationships in your data. One significant advantage of statsmodels is that it does not require reshaping the independent variable \(X\) into a 2D array, simplifying the workflow for regression analysis. In this section, we demonstrate how to use statsmodels to perform ordinary least squares (OLS) regression and extract detailed metrics like SST, SSR, SSE, and \(R^2\>.

Statsmodels provides comprehensive statistics for regression analysis, including detailed sum of squares components, standard errors, confidence intervals, and hypothesis tests. For more information, visit the official Statsmodels documentation.
statsmodels_implementation.py
import statsmodels.api as sm
import numpy as np

# Define data
hours = np.array([2, 4, 6, 8, 10])  # Independent variable
scores = np.array([65, 75, 85, 90, 95])  # Dependent variable
X = hours  # No need to reshape
y = scores

# Add constant for intercept
X_with_const = sm.add_constant(X)

# Fit the model
model_sm = sm.OLS(y, X_with_const).fit()

# Get sum of squares components
sst_sm = model_sm.centered_tss  # Total sum of squares
ssr_sm = model_sm.ess  # Explained sum of squares (Regression)
sse_sm = model_sm.ssr  # Sum of squared residuals (Error)
r2_sm = model_sm.rsquared

print("Statsmodels Results:")
print(f"SST: {sst_sm:.2f}")
print(f"SSR: {ssr_sm:.2f}")
print(f"SSE: {sse_sm:.2f}")
print(f"R²: {r2_sm:.4f}")

# Print detailed summary
print("\nDetailed Model Summary:")
print(model_sm.summary().tables[1])

Statsmodels Output:

Statsmodels Results:
SST: 580.00
SSR: 562.50
SSE: 17.50
R²: 0.9698

Detailed Model Summary:
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         59.5000      2.533     23.489      0.000      51.439      67.561
x1             3.7500      0.382      9.820      0.002       2.535       4.965
==============================================================================

Explanation of Metrics:

  • SST (Total Sum of Squares): The total variation in the dependent variable around its mean (580.00).
  • SSR (Regression Sum of Squares): The variation explained by the regression model (562.50).
  • SSE (Error Sum of Squares): The residual variation not explained by the model (17.50).
  • R² (Coefficient of Determination): Measures the proportion of variance explained by the model, showing a good fit (0.9698).

The detailed model summary provides additional information, such as:

  • Coefficients: The intercept (59.50) and slope (3.75) of the regression line, indicating the relationship between study hours and test scores.
  • Standard Errors: Quantify the uncertainty of the coefficients.
  • t-Statistic and P-Value: Test the statistical significance of the coefficients, confirming that both the intercept and slope are highly significant (P < 0.05).
  • Confidence Intervals: Provide a range within which the true coefficient values are likely to fall, with 95% confidence.

Advantages of Statsmodels OLS:

  • Comprehensive Diagnostics: Provides detailed statistical tests, such as t-tests and F-tests, to assess the significance and goodness-of-fit of the model.
  • Standard Errors and Confidence Intervals: Helps evaluate the reliability of the regression coefficients.
  • Detailed Model Summaries: Offers an extensive breakdown of regression results, including p-values and R-squared values.
  • No Need to Reshape \(X\): Unlike scikit-learn, statsmodels can handle 1D independent variables directly, simplifying the workflow.

Conclusion

In this comprehensive guide, we explored the concepts and calculations behind Total Sum of Squares (SST), Regression Sum of Squares (SSR), and Error Sum of Squares (SSE) in the context of regression analysis. We implemented these calculations in Python using both scikit-learn and statsmodels, providing not only a practical approach but also statistical insights to validate the regression model’s performance.

Understanding these metrics is crucial for evaluating how well a regression model explains the variability in your data. The relationship \( SST = SSR + SSE \) serves as a foundational check for verifying the correctness of calculations, while \(R^2\) offers an intuitive measure of the model’s fit. Through visualizations and step-by-step implementations, this guide has equipped you with the tools needed to interpret and analyze regression results effectively.

Key Takeaways:

  • SST, SSR, and SSE are essential components of regression analysis that quantify variance and error.
  • The relationship \( SST = SSR + SSE \) validates your calculations and the model’s logical consistency.
  • Visualizing these components helps illustrate the contributions of the model to explaining variability in the data.
  • scikit-learn is ideal for quick regression tasks, while statsmodels offers in-depth statistical insights.

If you’re interested in diving deeper into linear regression or exploring our regression tools, check out the Further Reading section.

Have fun and happy researching!

Further Reading

Expand your knowledge with these additional resources. Whether you’re looking for interactive tools or in-depth guides, these links will help you dive deeper into the concepts covered in this guide.

Attribution and Citation

If you found this guide and tools helpful, feel free to link back to this page or cite it in your work!

Buy Me a Coffee ✨

© 2024 The Research Scientist Pod. All rights reserved.