Implied volatility tells us the expected volatility of a stock over an option’s lifetime. Implied volatility is directly influenced by the supply and demand of the options and the market’s expectation of the direction of the price of the underlying security. As expectations rise or the demand for an option increases, implied volatility will increase. As implied volatility increases, the option price increases.
On the other hand, as the market’s expectations decrease or the demand for an option falls, implied volatility will also fall. As implied volatility decreases, the option price decreases.
This tutorial will go through an option’s implied volatility and how to calculate it with Python. We will consider root-finding methods to calculate implied volatility: Newton-Raphson, Interval Bisection, and Brute Force.
Table of contents
What is Implied Volatility?
Before going through implied volatility, you should have gone through the Black-Scholes formula and the Options Greeks.
We can use the Black-Scholes Formula to price a European option. We need five variables: stock price, exercise price, time to expiration, risk-free interest rate, and standard deviation of log returns or volatility. Let’s look at a diagram describing a European call option.
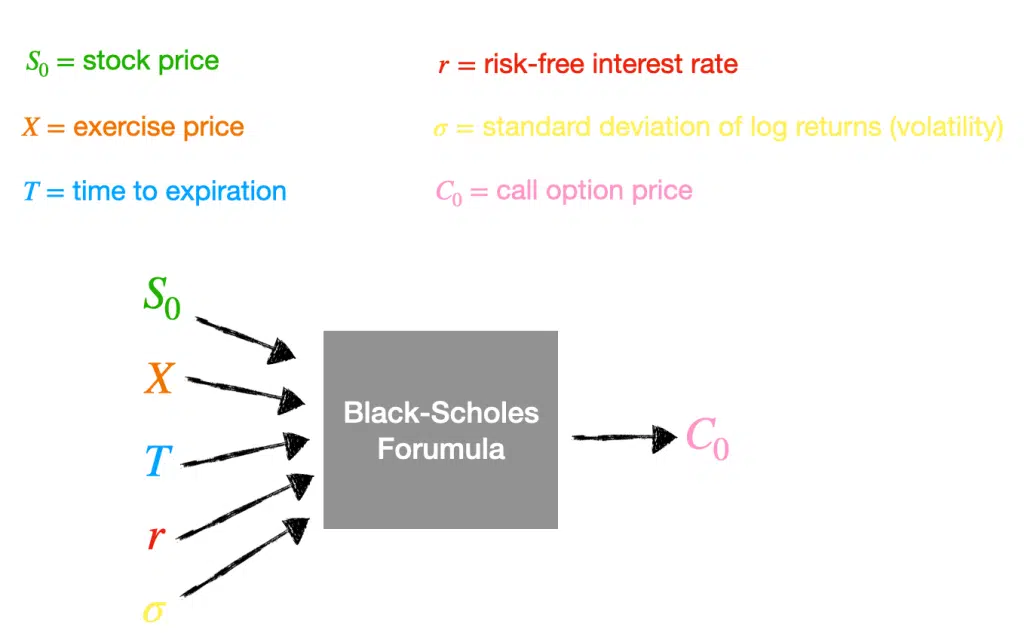
The first four variables are easy to find. We can easily find the stock price. The exercise price is part of the contract. We can approximate the risk-free interest rate by assuming it equals the interest rate on a three-month government Treasury bill. The time to expiration we can calculate using today’s date and when the contract will expire. However, volatility is tricky; it is not a constant value.
We can estimate the volatility of an option by looking at the history of the standard deviation of log returns.
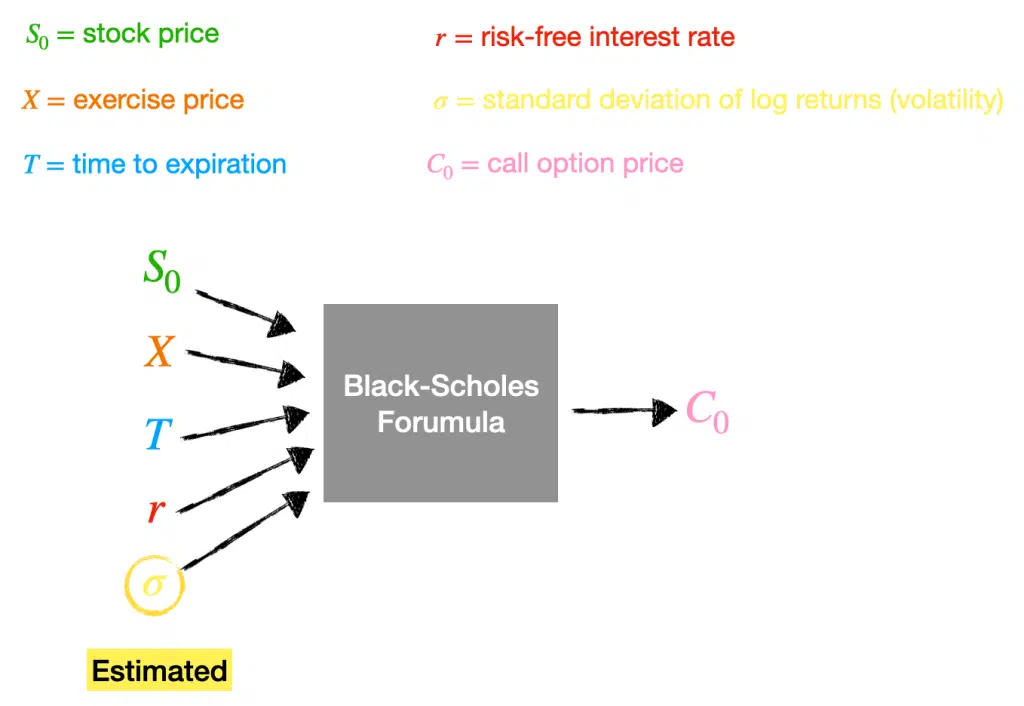
Any volatility value is an estimate, and there is an assumption that this variable will be constant over the option’s lifetime.
However, options are traded constantly, and we can look up the market price for a call option for a given stock price, exercise price, risk-free interest rate and time to expiration.
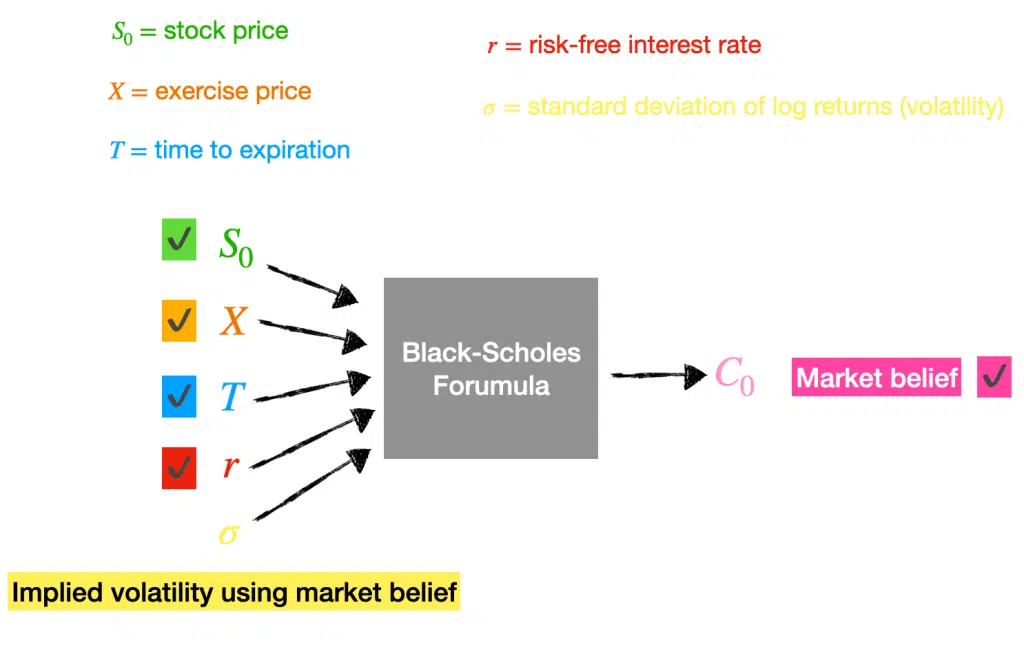
Suppose we know the market price or what the market believes the option price should be based on transactions and known variables. In that case, we can work backwards through Black-Scholes to determine the market estimate for the volatility or implied volatility.
If the market gets more unpredictable, the market will pay more for a given option, driving the implied volatility up. We can aggregate the implied volatility across multiple securities to find implied volatility for given markets at a time.
Remember, the implied volatility depends on an option’s market price, not the other way around.
Let’s look at the Black-Scholes formula for pricing a European call option:
$$C= S_{0}N(d_{1})~- Xe^{-r\tau}N(d_{2}) $$
where,
$$d_{1} = \frac{\text{ln}\frac{S_{0}}{X} + (r + \sigma^{2}/2)*\tau}{\sigma\sqrt{\tau}}, \qquad d_{2} = \frac{\text{ln}\frac{S_{0}}{X} + (r – \sigma^{2}/2)*\tau}{\sigma\sqrt{\tau}} = d_{1} – \sigma\sqrt{\tau}$$
- S: current underlying price
- K: strike price of option
- r: risk-free interest rate
- T: time until option expiration
- $\sigma: ~\text{annual volatility of underlying security’s returns}$
- N(x): cumulative distribution function for a standard normal distribution
Let’s say we want to find the implied volatility for an option with a current price for the underlying at \$100 for the right to buy the stock a year from the current date for \$125. The call option costs \$25, and the risk-free interest rate is 5%. If we put all of these values in the Black-Scholes formula, we will get the following:
$$25= 100 * N(\frac{\text{ln}\frac{100}{125} + (0.05 + \sigma^{2}/2)*1}{\sigma\sqrt{1}})~- 125e^{-0.05*1}N(\frac{\text{ln}\frac{100}{125} + (0.05 – \sigma^{2}/2)*1}{\sigma\sqrt{1}} $$
The unknown value in this equation is the volatility. We need to solve for volatility in the equation to return a call price of $18. We can solve this equation using iterative methods.
Now let’s look at the iterative methods to find the implied volatility in Python.
Implied volatility using Newton Raphson Method
The first method we will look at is the Newton-Raphson method. The Newton-Raphson method is a way to quickly find an approximation for the root of a real-valued function. The method considers that a straight-line tangent can approximate a continuous and differentiable function.
Newton Raphson Algorithm
- $\text{Define a continuous, differentiable function}~ f(x)$
- $\text{Take an initial guess for the root}~ x = x_{0},~\text{approximate the root guess with}~ x_{1} = \frac{f(x_{0})}{f'(x_{0})}.$
- $\text{Iterate as follows:}~ x_{n+1} = x_{n} – \frac{f(x_{n})}{f'(x_{n})}$
- $\text{Break if}~ |f(x_{n})| < \epsilon.~ \text{Where}~ \epsilon ~\text{is the tolerance for error}.$
When we apply the Newton-Raphson Algorithm to solve for implied volatility, we get the following:
- $\text{Our continuous, differentiable function is: }~f(\sigma) = V_{BS_{\sigma}} – V_{market}$
- $\text{Our initial guess is}~\sigma_{0} = 0.30$
- $\text{Iterate as follows:}~ \sigma_{n+1} = \sigma_{n} – \frac{V_{BS_{\sigma}} – V_{market}}{\frac{\partial V_{BS_{\sigma}}}{\partial \sigma}}$
- $\text{Break if}~ |V_{BS_{\sigma}} – V_{market}| < \epsilon,~ \text{return}~ \sigma_{n}.$
The Newton-Raphson algorithm converges fast.
Python Code for Newton-Raphson
First, we will define the cumulative distribution function and probability density function for a standard normal distribution.
import numpy as np from scipy.stats import norm N_prime = norm.pdf N = norm.cdf
Next, we will define the Black-Scholes function:
def black_scholes_func(S, K, T, r, sigma, cp):
'''
:param S: Asset price
:param K: Strike price
:param T: Time to maturity
:param r: risk-free rate (treasury bills)
:param sigma: volatility
:param cp: Call or Put
:return: call price
'''
# Black-Scholes Formula
d1 = (np.log(S / K) + (r + sigma ** 2 / 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
# Define
if cp:
price = S * N(d1) - N(d2)* K * np.exp(-r * T)
else:
price = K * np.exp(-r * T) * N(-1 * d2) - S*N(-1 * d1)
return price
Next, we will define the function for calculating the vega of an option:
def vega(S, K, T, r, sigma):
'''
:param S: Asset price
:param K: Strike price
:param T: Time to Maturity
:param r: risk-free rate (treasury bills)
:param sigma: volatility
:return: vega (partial derivative of value of option with respect to volatility)
'''
### calculating d1 from black scholes
d1 = (np.log(S / K) + (r + sigma ** 2 / 2) * T) / sigma * np.sqrt(T)
vega = S * np.sqrt(T) * N_prime(d1)
return vega
Now we can put it all together and find the implied volatility using the Newton-Raphson algorithm:
def implied_volatility_nr(C, S, K, T, r, cp, tol=0.0001,
max_iterations=100):
'''
:param C: Observed call price
:param S: Asset price
:param K: Strike Price
:param T: Time to Maturity
:param r: riskfree rate
:param tol: error tolerance in result
:param max_iterations: max iterations to update vol
:return: implied volatility in percent
'''
### assigning initial volatility estimate for input in Newton_rap procedure
sigma = 0.3
for i in range(max_iterations):
### calculate difference between blackscholes price and market price with
market_price = black_scholes_func(S, K, T, r, sigma, cp)
### iteratively updated volality estimate
diff = market_price - C
###break if difference is less than specified tolerance level
if abs(diff) < tol:
print(f'found on {i}th iteration')
print(f'difference is equal to {diff}')
break
print(diff)
### use newton rapshon to update the estimate
sigma = sigma - diff / vega(S, K, T, r, sigma)
return sigma
Let’s test the code for a call option
if __name__ == '__main__':
# Define option variables
obs_price = 25
S= 100
K=125
T=1
r=0.05
# Calculate implied volatility
imp_vol = implied_volatility_nr(obs_price, S, K, T, r, True)
print(f'Implied volatility using Newton Rapshon is: {imp_vol:.2f}%')
-19.308475812418376 1.5034061340488947 -0.004331994117166005 found on 3th iteration difference is equal to -3.2861052545740677e-08 Implied volatility using Newton Rapshon is: 79.18%
We found the implied volatility for the call option to be 79.18%.
If we plug the implied volatility value back into the Black-Scholes formula, we will get the market price for the call option:
if __name__ == '__main__':
# Define option variables
obs_price = 25
S= 100
K=125
T=1
r=0.05
# Calculate implied volatility
imp_vol_nr = implied_volatility_nr(obs_price, S, K, T, r, True)
price = black_scholes_func(S, K, T, r, imp_vol_nr/100, True)
print(f'option price using implied volatility from Newton-Raphson method is: ${price:.2f}'
Option price using implied volatility from Newton-Raphson method is: $25.00
Let’s test the code for the put option:
if __name__ == '__main__':
obs_price = 25
S= 100
K=125
T=1
r=0.05
# Put Implied volatility back into Black-Scholes
imp_vol = implied_volatility_nr(obs_price, S, K, T, r, False)
print(f'Implied volatility using Newton Rapshon is: {imp_vol:.2f}%')
-0.40479774982912886 0.0022461796047537064 found on 2th iteration difference is equal to 6.290173359957407e-08 Implied volatility using Newton Rapshon is: 31.11%
We found the implied volatility for the put option to be 31.11%.
If we plug the implied volatility value back into the Black-Scholes formula, we will get the market price for the put option:
if __name__ == '__main__':
obs_price = 25
S= 100
K=125
T=1
r=0.05
# Put Implied volatility back into Black-Scholes
imp_vol_nr = implied_volatility_nr(obs_price, S, K, T, r, True)
price = black_scholes_func(S, K, T, r, imp_vol_nr/100, True)
print(f'Option price using implied volatility from Newton-Raphson method is: ${price:.2f}'
Option price using implied volatility from Newton-Raphson method is: $25.00
Implied Volatility Using Interval Bisection Method
The second method we will look at is the Interval Bisection method. The interval bisection method does not require numerical derivatives to calculate the implied volatility.
Interval Bisection Algorithm
- $\text{Choose} ~\sigma_{a} ~\text{and} ~\sigma_{b} \text{with} ~\sigma_{a} < \sigma_{b} ~\text{and} ~\sigma_{b} – \sigma_{a} > \epsilon$
- $\text{Set}~ \sigma_{mid} := \frac{(\sigma_{a} + \sigma_{b})}{2}~ \text{and evaluate}~ BS_{\sigma_{mid}}$
- $\text{If}~ (BS_{\sigma_{mid}} – BS_{market}) > 0 ~\text{then}~ \sigma_{b} = \sigma_{mid}. ~\text{Otherwise reset}~ \sigma_{a} = \sigma_{mid}$
- $\text{If}~ \sigma_{b} – \sigma_{a} < \epsilon~ \text{then stop. Use}~ \frac{(\sigma_{a} + \sigma_{b})}{2} ~\text{as the approximation to the root of function. Otherwise return to Step 2.}$
Python code for Interval Bisection
Let’s look at the function to implement the interval bisection method:
def interval_bisection(c_market,a, b, epsilon, S, K, T, r, cp):
'''
:param c_market: Market price
:param a: Lower volatility bound
:param b: Upper volatility bound
:epsilon: Tolerance
:param S: Asset price
:param K: Strike Price
:param T: Time to Maturity
:param r: riskfree rate
:param cp: Call/Put
'''
x = (a + b ) * 0.5
maxiter = 100
while (b - a > epsilon):
x = (a+b)*0.5
price = black_scholes_func(S, K, T, r, x, cp)
if price - c_market > 0:
b = (a +b)/2
else:
a = (a + b)/2
return x* 100
Let’s apply the interval bisection method to a call option.
if __name__ == '__main__':
obs_price = 25
S= 100
K=125
T=1
r=0.05
a = 0.005
b = 1.15
epsilon = 0.0001
imp_vol = interval_bisection(obs_price, a, b, epsilon, S, K, T, r, True)
print(f'Implied volatility using Interval Bisection is: {imp_vol:.2f}%')
Implied volatility using Interval Bisection is: 79.18%
The implied volatility is 79.18%, the same value found using the Newton-Raphson method.
If we plug the implied volatility value back into the Black-Scholes formula, we will get the market price for the call option:
if __name__ == '__main__':
obs_price = 25
S= 100
K=125
T=1
r=0.05
a = 0.005
b = 1.15
epsilon = 0.0001
imp_vol_ib = interval_bisection(obs_price, a, b, epsilon, S, K, T, r, True)
price = black_scholes_func(S, K, T, r, imp_vol_ib/100, True)
print(f'Option price using implied volatility from Interval Bisection method is: ${price:.2f}')
Call price using implied volatility from Interval Bisection method method is: $25.00
Let’s apply the interval bisection method for a put option.
if __name__ == '__main__':
obs_price = 25
S= 100
K=125
T=1
r=0.05
a = 0.005
b = 1.15
epsilon = 0.0001
imp_vol = interval_bisection(obs_price, a, b, epsilon, S, K, T, r, False)
print(f'Implied volatility using Interval Bisection is: {imp_vol:.2f}%')
Implied volatility using Interval Bisection is: 31.10%
We can see the implied volatility is 31.10%, which is the same value found using the Newton-Raphson method.
If we plug the implied volatility value back into the Black-Scholes formula, we will get the market price for the call option:
if __name__ == '__main__':
obs_price = 25
S= 100
K=125
T=1
r=0.05
a = 0.005
b = 1.15
epsilon = 0.0001
# Put Implied volatility back into Black-Scholes
imp_vol_ib = interval_bisection(obs_price, a, b, epsilon, S, K, T, r, False)
price = black_scholes_func(S, K, T, r, imp_vol_ib/100, False)
print(f'Put price using implied volatility from Interval Bisection method is: ${price:.2f}')
Put price using implied volatility from Interval Bisection method method is: $25.00
Implied Volatility Using Brute Force Method
The brute force method iterates through possible volatility candidates and finds the value that minimizes the absolute difference between the market price and the calculated Black-Scholes price or the root of the function.
Brute Force Algorithm
- $\text{Define threshold}~\epsilon~\text{for when to accept the solution, e.g. when calculated price and actual market price within 1 cent}$
- $\text{Define step variable to adjust the}~ \sigma ~\text{value}$
- $\text{Take an initial guess for}~ \sigma$
- $\text{If} ~BS_{market} – BS_{\sigma} > \epsilon~\text{ then}~ \sigma = \sigma + \text{step}.$
- $\text{Else if} ~BS_{market} – BS_{\sigma} < 0 ~\text{and}~ | BS_{market} – BS_{\sigma}| > \epsilon~\text{, then}~ \sigma = \sigma – \text{step}.$
- $\text{Else if} ~|BS_{market} – BS_{\sigma}| < \epsilon\text{, then}~ \text{choose} ~\sigma~ \text{as root of function}.$
Python Code for Brute Force
Let’s look at the code for the brute force method:
def brute_force(c_market, S, K, T, r, cp):
'''
:param c_market: Market price
:param S: Asset price
:param K: Strike Price
:param T: Time to Maturity
:param r: riskfree rate
:param cp: Call/Put
'''
_sigma = 0.5
one_cent = 0.0001
step = 0.0001
for i in range(10000):
price = black_scholes_func(S, K, T, r, _sigma, cp)
diff = c_market - price
if diff > one_cent:
_sigma = _sigma + step
elif diff < 0 and abs(diff) > one_cent:
_sigma = _sigma - step
elif abs(diff) < one_cent:
return _sigma * 100
return _sigma * 100
Let’s apply the brute force method to the call option:
if __name__ == '__main__':
obs_price = 25
S= 100
K=125
T=1
r=0.05
# Calculate Implied Volatility using Brute force
imp_vol_bf = brute_force(obs_price, S, K, T, r, True)
print(f'Implied volatility using Brute Force is: {imp_vol_bf:.2f}%')
Implied volatility using Brute Force is: 79.18%
The implied volatility is 79.18%, the same as the values found by the Newton-Raphson and Interval Bisection methods.
If we plug the implied volatility value back into the Black-Scholes formula, we will get the market price for the call option:
if __name__ == '__main__':
obs_price = 25
S= 100
K=125
T=1
r=0.05
# Put Implied volatility back into Black-Scholes
imp_vol_bf = brute_force(obs_price, S, K, T, r, True)
price = black_scholes_func(S, K, T, r, imp_vol_bf/100, True)
print(f'Option price using implied volatility from brute force method is: ${price:.2f}')
Option price using implied volatility from brute force method is: $25.00
Let’s apply the brute force method to the put option:
if __name__ == '__main__':
obs_price = 25
S= 100
K=125
T=1
r=0.05
# Calculate Implied Volatility using Brute force
imp_vol_bf = brute_force(obs_price, S, K, T, r, False)
print(f'Implied volatility using Brute Force is: {imp_vol_bf:.2f}%')
Implied volatility using Newton Rapshon is: 31.10%
The implied volatility is 31.10%, the same as the values found by the Newton-Raphson and Interval Bisection methods.
If we plug the implied volatility value back into the Black-Scholes formula, we will get the market price for the put option:
if __name__ == '__main__':
obs_price = 25
S= 100
K=125
T=1
r=0.05
# Put Implied volatility back into Black-Scholes
imp_vol_bf = brute_force(obs_price, S, K, T, r, False)
call_price = black_scholes_func(S, K, T, r, imp_vol_bf/100, False)
print(f'Call price using implied volatility from brute force method is: ${call_price:.2f}')
Call price using implied volatility from brute force method is: $25.00
The brute force method is the slowest method out of the three.
If you want to learn how to calculate implied volatility in Python and C++, go to the articles:
Summary
Congratulations on reading to the end of this tutorial!
Go to the online courses page on Python to learn more about coding in Python for data science and machine learning.
For further reading on the Options Greeks, go to the article:
You can use our free Black-Scholes option pricing calculator to estimate the fair value of a European call or put option.
You can use our free Implied Volatility calculator to estimate the Implied Volatility of a priced option.
Have fun, and happy researching!
Suf is a senior advisor in data science with deep expertise in Natural Language Processing, Complex Networks, and Anomaly Detection. Formerly a postdoctoral research fellow, he applied advanced physics techniques to tackle real-world, data-heavy industry challenges. Before that, he was a particle physicist at the ATLAS Experiment of the Large Hadron Collider. Now, he’s focused on bringing more fun and curiosity to the world of science and research online.

