How to Calculate Mean Absolute Deviation (MAD) in R with Practical Examples

Mean Absolute Deviation (MAD) is a metric used to measure the spread or variability in a dataset. MAD represents the average absolute deviation of each data point from the mean of the dataset, making it easy to interpret. In this post, we’ll explore how to calculate MAD in R, using examples with vectors and data frames. We’ll also create a custom MAD function for reusability and discuss visualization techniques.

What is Mean Absolute Deviation (MAD)?

Mean Absolute Deviation (MAD) is defined as:

\[ \text{MAD} = \frac{1}{n} \sum_{i=1}^{n} |x_i – \bar{x}| \]

where:

• \( n \) is the number of observations,
• \( x_i \) is the value of the \( i \)-th observation,
• \( \bar{x} \) is the mean of all observations.

MAD is a straightforward measure of spread, providing insights into how much values in a dataset differ from the average. It’s especially helpful when comparing distributions, as it is not affected by outliers as strongly as other metrics like standard deviation.

Example 1: Calculating MAD for a Simple Vector

Let’s start with a simple example to calculate MAD for a vector of numbers. Consider the following hypothetical data representing observations of a variable:

# Sample data
data <- c(10, 12, 23, 23, 16, 18, 12, 10, 15, 17)

To calculate MAD, we’ll first find the mean, compute the absolute deviations from the mean, and then average these deviations.

# Step 1: Calculate the mean of the data
mean_data <- mean(data)

# Step 2: Calculate the absolute deviations from the mean
absolute_deviations <- abs(data - mean_data)

# Step 3: Calculate the mean of the absolute deviations
mad <- mean(absolute_deviations)
mad

Running this code gives us the MAD value:

[1] 3.8

This MAD value of 3.8 indicates that, on average, the data points deviate by 3.8 units from the mean. This provides an intuitive sense of the variability in our data.

Example 2: MAD Calculation for a Data Frame Column

Now, let’s calculate MAD for a column in a data frame. Suppose we have the following dataset:

# Sample data frame
df <- data.frame(
  observation = 1:10,
  value = c(10, 12, 23, 23, 16, 18, 12, 10, 15, 17)
)

# Display the data frame
print(df)

   observation value
1            1    10
2            2    12
3            3    23
4            4    23
5            5    16
6            6    18
7            7    12
8            8    10
9            9    15
10          10    17

We’ll calculate MAD for the value column using similar steps as before:

# Calculate the mean of the 'value' column
mean_value <- mean(df$value)

# Calculate the absolute deviations from the mean
absolute_deviations <- abs(df$value - mean_value)

# Calculate the mean of the absolute deviations
mad_value <- mean(absolute_deviations)
mad_value

This outputs the MAD for the value column:

[1] 3.8

Similar to our vector example, the MAD value here tells us the average deviation from the mean for observations in the value column.

Visualizing Mean Absolute Deviation

Visualizations are helpful to understand how data points are distributed around the mean. We can create a plot of the data points with a reference line at the mean, as well as dashed lines indicating ± the Mean Absolute Deviation (MAD).

# Load necessary libraries
library(ggplot2)

# Calculate mean and MAD
mean_value <- mean(df$value)
mad_value <- mean(abs(df$value - mean_value))

# Plot with mean and MAD lines
ggplot(df, aes(x = observation, y = value)) +
  geom_point(color = "blue", size = 3) +
  geom_hline(aes(yintercept = mean_value, color = "Mean"), linetype = "solid", size = 1) +
  geom_hline(aes(yintercept = mean_value + mad_value, color = "Mean ± MAD"), linetype = "dashed") +
  geom_hline(aes(yintercept = mean_value - mad_value, color = "Mean ± MAD"), linetype = "dashed") +
  scale_color_manual(values = c("Mean" = "red", "Mean ± MAD" = "purple")) +
  labs(title = "Data Points with Mean and Mean Absolute Deviation",
       x = "Observation",
       y = "Value",
       color = "Legend") +
  theme_minimal() +
  theme(plot.title = element_text(hjust = 0.5))

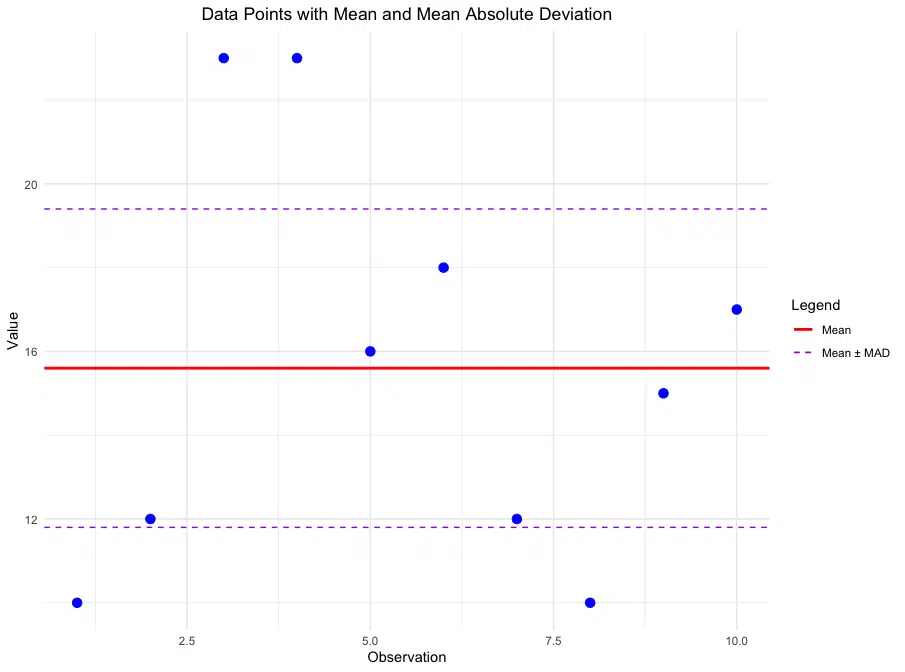
In this plot:

• The solid red line represents the mean of the dataset.
• The dashed purple lines represent the mean ± the Mean Absolute Deviation (MAD), showing the range around the mean within which most data points are expected to lie, on average. This range provides an intuitive view of the typical spread of values, indicating how much data points tend to deviate from the mean without overemphasizing outliers.

Creating a Custom MAD Function in R

To streamline the calculation of MAD, let’s create a custom function that can be applied to any vector of values. This function will help make MAD calculation quick and reusable.

# Define a custom MAD function
calculate_mad <- function(x) {
  mean_absolute_deviation <- mean(abs(x - mean(x)))
  return(mean_absolute_deviation)
}

# Test the function
mad_result <- calculate_mad(df$value)
mad_result

Using calculate_mad() on our data frame column provides the MAD value, making it easy to reuse on any data vector.

[1] 3.8

Assumptions and Limitations

When using Mean Absolute Deviation (MAD) as a measure of spread in R, it’s important to understand the assumptions behind this metric, as well as its limitations. Here’s a breakdown of key points to consider when interpreting MAD in data analysis:

Assumptions

• Non-Sensitivity to Extreme Values: MAD is typically used when the goal is to measure variability in a way that is less sensitive to outliers. Unlike standard deviation, which squares differences and amplifies the effect of large deviations, MAD treats all deviations equally by taking the absolute value. This makes it suitable for datasets where outliers might distort other measures of spread.
• Data Representing a Single Population: The MAD calculation assumes that all data points come from a single population. If data points represent different groups or categories, the MAD may not accurately reflect the spread within each group. In such cases, it’s better to calculate MAD for each group separately.
• Symmetric Deviations Around the Mean: MAD assumes that deviations around the mean are somewhat symmetric. If the data distribution is heavily skewed, the MAD might not be as informative, as it does not account for directional skew. For heavily skewed data, other spread measures like the median absolute deviation (MAD based on the median) may be more appropriate.

Limitations

• Ignores the Direction of Deviations: Since MAD uses the absolute values of deviations, it doesn’t indicate whether data points are consistently above or below the mean. This lack of directional information may limit its interpretability in cases where understanding whether deviations are positive or negative is important.
• Limited Sensitivity to Outliers: While the insensitivity to outliers can be beneficial, it also limits MAD’s ability to capture large deviations from the mean, which may be meaningful in some analyses. For datasets where outliers are important or highly relevant, MAD may not provide a complete picture of variability.
• Not Ideal for Normally Distributed Data: MAD is generally not the best choice when the data follows a normal distribution. In such cases, standard deviation is often preferred, as it aligns with properties of the normal distribution, providing a more informative measure of spread.
• Comparability with Other Metrics: MAD is less commonly used than standard deviation and may not be directly comparable to other measures of spread. For example, in models that rely on the variance of data (such as linear regression), standard deviation is more commonly applied. MAD may not provide insights that are directly useful in contexts that rely on variance-based measures.
• Assumes Mean as the Central Tendency: MAD, as calculated here, assumes that the mean is the measure of central tendency. If a dataset has significant skew, it may be more appropriate to calculate the median absolute deviation (MAD about the median) to reflect spread around the median, which is often a better representation of central tendency for skewed data.

Practical Considerations

While MAD is an intuitive and useful measure for certain datasets, it’s best suited for:

• Situations where outliers should not disproportionately affect the measure of spread.
• Data distributions that do not follow a normal pattern, where absolute deviations offer clearer insights than squared deviations.

For a robust analysis, consider pairing MAD with other metrics, such as standard deviation or median absolute deviation, to gain a more comprehensive view of data spread and variability.

Conclusion

Mean Absolute Deviation (MAD) is a valuable measure of variability, offering insight into the average deviation of observations from the mean. By calculating MAD in R, we can effectively understand data spread, which can help with model evaluation and data analysis.

This post covered the fundamentals of MAD, illustrated its calculation with practical examples, and provided a reusable function for future analysis. By integrating MAD into your data analysis workflow, you gain a reliable, intuitive measure for assessing the dispersion in datasets.

Try the Mean Absolute Deviation Calculator

If you’d like to calculate Mean Absolute Deviation Calculator quickly for your own data, check out our Mean Absolute Deviation Calculator on the Research Scientist Pod.

Have fun and happy researching!