How to Calculate Median Absolute Deviation (MAD) in R with Practical Examples

Median Absolute Deviation (MAD) is a robust measure of variability that is less influenced by outliers compared to other metrics like standard deviation or mean absolute deviation. MAD measures the median distance of data points from the median of the dataset, making it highly useful for skewed or non-normal data distributions. This guide will explain how to calculate MAD in R, use practical examples, and leverage R’s built-in mad() function.

What is Median Absolute Deviation (MAD)?

Median Absolute Deviation (MAD) is defined as:

\[ \text{MAD} = \text{median}(|x_i – \tilde{x}|) \]

where:

• \( x_i \) is the value of the \( i \)-th observation,
• \( \tilde{x} \) is the median of all observations.

This metric provides an idea of how much each data point deviates from the median. Because it uses the median rather than the mean, it is more resistant to the effects of outliers and is particularly helpful for datasets with skewed distributions.

Example 1: Calculating MAD for a Simple Vector

Let’s start with a simple example to calculate MAD for a vector of numbers. Consider the following hypothetical data representing observations of a variable:

# Sample data
data <- c(10, 12, 23, 23, 16, 18, 12, 10, 15, 17)

To calculate MAD, we’ll first find the median, compute the absolute deviations from the median, and then take the median of those deviations.

# Step 1: Calculate the median of the data
median_data <- median(data)

# Step 2: Calculate the absolute deviations from the median
absolute_deviations <- abs(data - median_data)

# Step 3: Calculate the median of the absolute deviations
mad <- median(absolute_deviations)
mad

Running this code gives us the MAD value:

[1] 3.5

This MAD value of 3.5 tells us that the typical distance of each data point from the median is 3.5 units. This provides an intuitive sense of the spread of values around the median.

Example 2: MAD Calculation for a Data Frame Column

Now, let’s calculate MAD for a column in a data frame. Suppose we have the following dataset:

# Sample data frame
df <- data.frame(
  observation = 1:10,
  value = c(10, 12, 23, 23, 16, 18, 12, 10, 15, 17)
)

# Display the data frame
print(df)

   observation value
1            1    10
2            2    12
3            3    23
4            4    23
5            5    16
6            6    18
7            7    12
8            8    10
9            9    15
10          10    17

We’ll calculate MAD for the value column using similar steps as before:

# Calculate the median of the 'value' column
median_value <- median(df$value)

# Calculate the absolute deviations from the median
absolute_deviations <- abs(df$value - median_value)

# Calculate the median of the absolute deviations
mad_value <- median(absolute_deviations)
mad_value

This outputs the MAD for the value column:

[1] 3.5

As with our vector example, the MAD value indicates the typical deviation of each data point from the median for observations in the value column.

Visualizing Median Absolute Deviation

Visualizing MAD can help us see how data points are distributed around the median. We can create a plot of the data points with a reference line at the median, as well as dashed lines indicating ± the Median Absolute Deviation (MAD).

# Load necessary libraries
library(ggplot2)

# Calculate median and MAD
median_value <- median(df$value)
mad_value <- median(abs(df$value - median_value))

# Plot with median and MAD lines
ggplot(df, aes(x = observation, y = value)) +
  geom_point(color = "blue", size = 3) +
  geom_hline(aes(yintercept = median_value, color = "Median"), linetype = "solid", size = 1) +
  geom_hline(aes(yintercept = median_value + mad_value, color = "Median ± MAD"), linetype = "dashed") +
  geom_hline(aes(yintercept = median_value - mad_value, color = "Median ± MAD"), linetype = "dashed") +
  scale_color_manual(values = c("Median" = "red", "Median ± MAD" = "purple")) +
  labs(title = "Data Points with Median and Median Absolute Deviation",
       x = "Observation",
       y = "Value",
       color = "Legend") +
  theme_minimal() +
  theme(plot.title = element_text(hjust = 0.5))

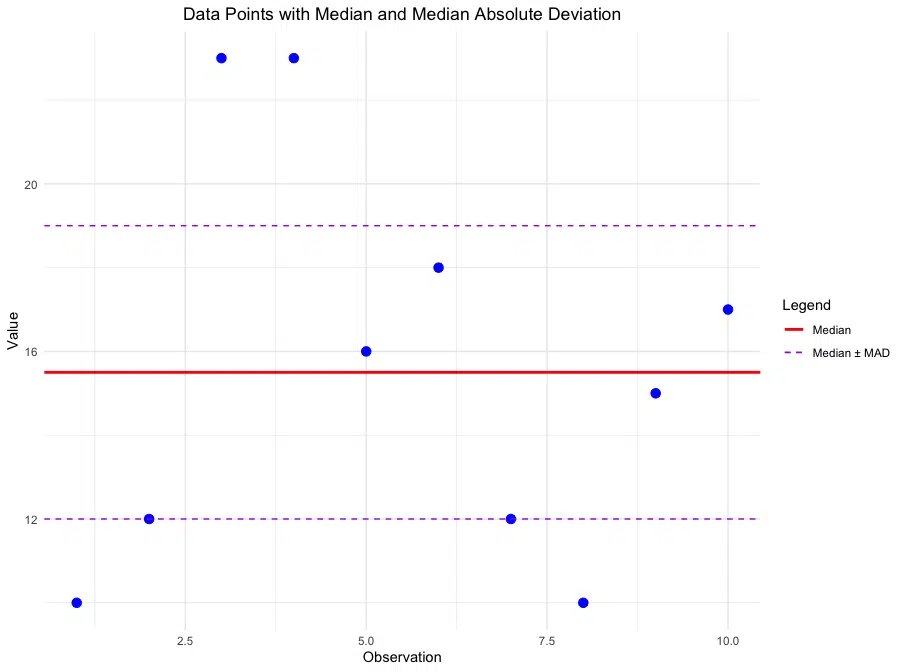
In this plot:

• The solid red line represents the median of the dataset.
• The dashed purple lines represent the median ± the Median Absolute Deviation (MAD), showing the range around the median within which most data points are expected to lie, on average. This range provides an intuitive view of the data's typical spread around the central value, offering a robust measure of variability that is less affected by outliers and skewed data than metrics based on the mean.

Using R’s Built-in mad() Function

R provides a convenient built-in function, mad(), to calculate the median absolute deviation. By default, this function calculates MAD about the median with a scaling constant, making it a quick and efficient way to measure variability.

# Using R's built-in mad() function
mad_value_builtin <- mad(df$value)
mad_value_builtin

[1] 5.1891

This output gives the MAD for the value column, scaled by a factor of 1.4826 (default in R) to make it comparable to the standard deviation in normally distributed data. You can adjust this by setting constant = 1 if you want the exact median absolute deviation without scaling.

# Using R's built-in mad() function with constant = 1
mad_value_builtin <- mad(df$value, constant=1)
mad_value_builtin

[1] 3.5

Assumptions and Limitations

When using Median Absolute Deviation (MAD), it’s important to understand its assumptions and limitations:

Assumptions

• Robustness to Outliers: MAD is chosen for its resistance to outliers. Unlike the mean, which can be skewed by extreme values, the median focuses on the central tendency of the data.
• Single-Population Representation: MAD assumes all data points are from a single population. If data points represent different groups, calculate MAD separately for each group.

Limitations

• Directional Information Lost: Like the mean absolute deviation, MAD does not show whether deviations are positive or negative, which may limit interpretability in some cases.
• Not Comparable to Variance-Based Metrics: MAD is not directly comparable to variance or standard deviation, particularly without scaling.

Conclusion

Median Absolute Deviation (MAD) is a useful, robust measure of variability, ideal for skewed or outlier-prone datasets. By leveraging R’s mad() function, you can efficiently calculate MAD and gain insights into data spread around the median.

Have fun and happy researching!

Try the Median Absolute Deviation Calculator

If you’d like to calculate Median Absolute Deviation Calculator quickly for your own data, check out our Median Absolute Deviation Calculator on the Research Scientist Pod.

Have fun and happy researching!