How to Calculate the Manhattan Distance in Python

Distances measures are essential tools for machine learning. A distance measure is a score that summarises how different two objects are in the problem domain. Usually, we calculate distance measures on rows of data, like strings representing text documents. Specific algorithms use distance measures, such as K-means, which uses a distance metric to assign data points to centroids. We will introduce and explore the Manhattan distance, also known as the Taxicab distance or the City Block distance.

What is the Manhattan Distance?

The Manhattan distance calculates the distance between two real-valued vectors in a grid-like path. You can visualize this grid-like chessboard or the plan view of city blocks. The Taxicab alias refers to the behaviour of a taxicab going to a destination; it would take the shortest path between city blocks, which are coordinates on the grid. Let’s take a simple example of a plane with two data points p_1 at Cartesian coordinates x_1, y_1 and p_2 at Cartesian coordinates x_2, y_2:

The Manhattan distance for the two-coordinate system is:

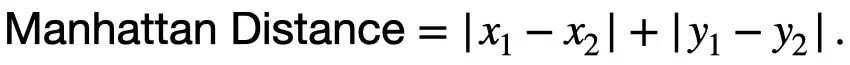
In an N-dimensional space, we can represent two points p_1 and p_2 as x_1, x_2, …, x_N and y_1, y_2, …, y_N. Then, the Manhattan distance between p_1 and p_2 is:

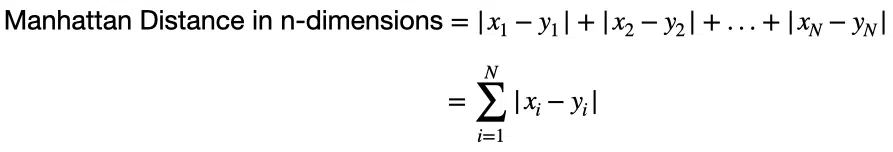
In other words, the Manhattan distance is the sum of absolute differences between points across all dimensions.

Difference Between Manhattan and Euclidean Distance

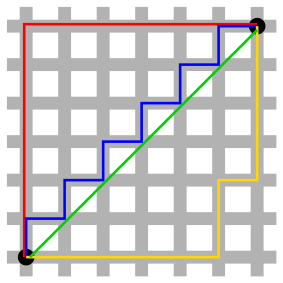
The axial constraints are the difference between the Manhattan and Euclidean distances.

Euclidean distance is the shortest path between two points, the green line as shown in the figure above.

Manhattan distance determines the shortest path parallel to the coordinate axes system, which in the figure above is Cartesian. Therefore, the path calculated may not be the straight line as with Euclidean distance.

Manhattan Distance is the sum of all the differences between the two points indicated by the red, yellow and blue paths in the figure above, each with the same shortest path. In Euclidean geometry, the green line is the unique shortest path between the two points.

As the Manhattan distance only moves along the axes, it has to move further than the Euclidean distance. Therefore the Manhattan distance is never shorter than the Euclidean distance between two points.

Practical Differences between Manhattan and Euclidean Distances

For high-dimensional data problems, the Manhattan distance is preferred over the Euclidean distance metric. This preference arises because high-dimensional data is sparse, making tasks such as clustering and nearest neighbor search more challenging, as the distance between objects becomes uniform and thus less meaningful. This phenomenon of uniform distance in high dimensions is more pronounced for the Euclidean distance than for the Manhattan distance.

Distance metric or matching criteria is the primary tool for retrieving similar images. In content-based image retrieval systems, both Manhattan and Euclidean distances are proposed by research to determine the similarity between pairs of facial images as feature vectors. Different categories of faces have different expressions and angles. Experimental results have shown that Manhattan distance performs better than Euclidean distance for matching similar images.

Calculating the Manhattan Distance Between Vectors

Python provides several libraries we can use to calculate the Manhattan distance and other distance metrics. Let’s look at using the built-in function abs() and sqrt() from the math module.

# Calculating the Manhattan Distance Manually

# Get sqrt function

from math import sqrt

# Define function

def manhattan_distance(x, y):

   return sum(abs(i1-i2) for i1, i2 in zip(x,y))

# Provide input vectors 

vector_1 = [2, 3, 49, 10, 15]

vector_2 =[9, 12, 20, 5, 1]

# Calculate the Manhattan Distance

distance = manhattan_distance(vector_1, vector_2)

# Print result

print(distance)

64

The above code contains a custom function that takes to vectors as input. The function returns the sum of the absolute differences between all element pairs between the two vectors.

We define two vectors as arrays of integers and then calculate the Manhattan distance between them.

We can perform the same calculation using the cityblock() function from SciPy, which requires fewer lines of code.

# Calculating the Manhattan Distance using SciPy

# Get cityblock function

from scipy.spatial.distance import cityblock

# Provide input vectors
vector_1 = [2, 3, 49, 10, 15]

vector_2 = [9, 12, 20, 5, 1]

#Calculate the Manahattan Distance
distance_scipy = cityblock(vector_1, vector_2)

#Print result
print(distance_scipy)

64

Running the SciPy version produces the same result, confirming the custom implementation. Performing calculations by hand is beneficial for learning the mathematics behind the value you are trying to obtain. However, importing a library with the relevant function will save time and is easier to implement.

Applications of Manhattan Distancce

We can use Manhattan distance in:

• Regression analysis, where its use dates back to the 18th century and is referred to as LASSO.
• Compressed sensing: We can employ compressed sensing theory to compress neural signals. To do so researchers have successfully employed the use of a minimum Euclidean or Manhattan Distance Cluster-based (MDC) deterministic compressed sensing matrix The MDC matrix can largely compress neural signals and also have a small reconstruction error.
• Differences between discrete frequency distributions, for example in RNA splicing, the positional distributions of hexamers can be compared with the Manhattan Distance. Each distribution is a vector, with each entry being a hexamer starting at a certain nucleotide. A large Manhattan distance would indicate a significant difference between two distributions and a small distance would indicate similarly shaped distributions.
• Clustering and nearest neighbour algorithms, like kNN, which use distance metrics to find the distance between points in a dataset.
• For an n-dimensional hypercube, where the vertices are binary strings, the Hamming distance of the strings is equivalent to the Manhattan distance between the vertices. Hypercubes are tools in graph theory.

Summary

Congratulations on reading to the end of this article. The Manhattan Distance, also known as Taxicab or City Block distance, is the sum of the absolute differences between two vectors or points on an n-dimensional plane. The Taxicab name refers to the intuition of a taxi taking the shortest path from origin to a destination within the constraints of city blocks. For example, the cab cannot drive through a building to get to a destination faster. We can calculate the Manhattan Distance manually or using a pre-built function in scientific libraries like SciPy. Manhattan Distance is a distance measure vital for machine learning algorithms that use distance measures like the k-nearest neighbors algorithm.

For more mathematical implementations in Python, go to the article: How to Write the Fibonacci Sequence in Python.

You can learn more about distance metrics in data science by visiting the online courses page.

Have fun and happy researching!