Introduction
This comprehensive guide demonstrates various methods to calculate Sum of Squares components (SST, SSR, and SSE) in R. We’ll explore implementations using base R, tidyverse, and the stats package, providing clear examples and visualizations for each approach.
Table of Contents
Mathematical Foundations
Total Sum of Squares (SST)
SST measures the total variation in the dependent variable (y) around its mean. It represents the total amount of variability in the data:
Formula:
\[ SST = \sum(y_i – \bar{y})^2 \]
Where:
- \( y_i \) = each observed value
- \( \bar{y} \) = the mean of all observed values
This value is always positive because it sums the squared differences between the observed values and their mean.
Regression Sum of Squares (SSR)
SSR quantifies the variation explained by the regression model:
Formula:
\[ SSR = \sum(\hat{y}_i – \bar{y})^2 \]
Where:
- \( \hat{y}_i \) = each predicted value
- \( \bar{y} \) = the mean of the observed values
A higher SSR indicates that the regression model explains a large proportion of the variability in the data.
Error Sum of Squares (SSE)
SSE measures the unexplained variation:
Formula:
\[ SSE = \sum(y_i – \hat{y}_i)^2 \]
Where:
- \( y_i \) = each observed value
- \( \hat{y}_i \) = each predicted value
Lower SSE indicates better model fit.
The Fundamental Relationship
\[ SST = SSR + SSE \]
This relationship shows how total variation splits between explained and unexplained components.
Coefficient of Determination (R²)
\[ R^2 = \frac{SSR}{SST} = 1 – \frac{SSE}{SST} \]
Interpretation:
- \( R^2 = 1 \): Perfect model fit
- \( R^2 = 0 \): Model explains no variance
- Higher \( R^2 \) indicates better fit
Implementation in Base R
Base R provides a straightforward way to compute Sum of Squares components (SST, SSR, and SSE) using simple functions and operations. This section walks you through a step-by-step implementation using an example dataset.
Step-by-Step Code
# Step 1: Create the dataset
hours <- c(2, 4, 6, 8, 10) # Independent variable
scores <- c(65, 75, 85, 90, 95) # Dependent variable
# Step 2: Fit the regression model
model <- lm(scores ~ hours) # Linear regression model
# Step 3: Compute the mean of the dependent variable
y_mean <- mean(scores)
# Step 4: Get the predicted values from the model
y_pred <- predict(model)
# Step 5: Calculate SST (Total Sum of Squares)
sst <- sum((scores - y_mean)^2)
# Step 6: Calculate SSR (Regression Sum of Squares)
ssr <- sum((y_pred - y_mean)^2)
# Step 7: Calculate SSE (Error Sum of Squares)
sse <- sum((scores - y_pred)^2)
# Step 8: Compute R-squared
r_squared <- ssr / sst
# Step 9: Print results
cat("SST:", sst, "\n")
cat("SSR:", ssr, "\n")
cat("SSE:", sse, "\n")
cat("R-squared:", r_squared, "\n")Detailed Explanation
Let's break down each step in the implementation:
-
Step 1: Create the dataset
The variables
hours(independent variable) andscores(dependent variable) represent the study hours and test scores, respectively. -
Step 2: Fit the regression model
The
lm()function fits a linear regression model to the data, withscoresas the dependent variable andhoursas the independent variable. -
Step 3: Compute the mean of the dependent variable
The mean of the dependent variable
scoresis calculated usingmean(). This value (\( \bar{y} \)) is used in SST and SSR calculations. -
Step 4: Get the predicted values
The predicted values (\( \hat{y}_i \)) are obtained using the
predict()function, which applies the fitted model to the data. -
Step 5: Calculate SST
SST is computed as the sum of squared differences between the observed values and their mean: \[ SST = \sum(y_i - \bar{y})^2 \]
-
Step 6: Calculate SSR
SSR is the sum of squared differences between the predicted values and the mean of the observed values: \[ SSR = \sum(\hat{y}_i - \bar{y})^2 \]
-
Step 7: Calculate SSE
SSE is the sum of squared differences between the observed and predicted values: \[ SSE = \sum(y_i - \hat{y}_i)^2 \]
-
Step 8: Compute \( R^2 \)
The coefficient of determination (\( R^2 \)) is calculated as: \[ R^2 = \frac{SSR}{SST} \]
-
Step 9: Print results
The results for SST, SSR, SSE, and \( R^2 \) are displayed using the
cat()function.
Example Output
Key Takeaways
- Base R provides all the tools needed to compute SST, SSR, and SSE without relying on additional libraries.
- The relationship \( SST = SSR + SSE \) holds true, confirming the calculations.
- High \( R^2 \) values (close to 1) indicate that the model explains most of the variability in the data.
Implementation with Tidyverse
The Tidyverse is a collection of R packages designed for data science workflows, providing an intuitive and pipeline-friendly approach to data manipulation and analysis. In this section, we’ll compute SST, SSR, and SSE using Tidyverse functions.
Step-by-Step Code
# Step 1: Load the required library
library(tidyverse)
# Step 2: Create a tibble with the data
df <- tibble(
hours = c(2, 4, 6, 8, 10), # Independent variable
scores = c(65, 75, 85, 90, 95) # Dependent variable
)
# Step 3: Fit the regression model
model_tidy <- lm(scores ~ hours, data = df)
# Step 4: Add predictions and components to the tibble
df <- df %>%
mutate(
predicted = predict(model_tidy), # Predicted values
mean_score = mean(scores), # Mean of observed values
sst_comp = (scores - mean_score)^2, # SST components
ssr_comp = (predicted - mean_score)^2, # SSR components
sse_comp = (scores - predicted)^2 # SSE components
)
# Step 5: Calculate SST, SSR, SSE, and R-squared
results <- df %>%
summarise(
sst = sum(sst_comp), # Total Sum of Squares
ssr = sum(ssr_comp), # Regression Sum of Squares
sse = sum(sse_comp), # Error Sum of Squares
r_squared = ssr / sst # Coefficient of Determination
)
# Step 6: Print results
print(results)Detailed Explanation
Here’s a breakdown of the Tidyverse workflow:
-
Step 1: Load the Tidyverse library
The
tidyversepackage includes functions for data manipulation (dplyr) and creating tibbles (tibble), among others. Load it usinglibrary(tidyverse). -
Step 2: Create a tibble
A tibble is a modern version of a dataframe, offering better printing and compatibility with Tidyverse functions. The tibble contains two columns:
hours(independent variable) andscores(dependent variable). -
Step 3: Fit the regression model
The
lm()function fits a linear regression model. Here,scoresis the dependent variable, andhoursis the independent variable. -
Step 4: Add predictions and components
Using
mutate(), new columns are added to the tibble:predicted: Predicted values (\( \hat{y}_i \)) from the regression model.mean_score: Mean of the dependent variable (\( \bar{y} \)).sst_comp: Components for SST (\( (y_i - \bar{y})^2 \)).ssr_comp: Components for SSR (\( (\hat{y}_i - \bar{y})^2 \)).sse_comp: Components for SSE (\( (y_i - \hat{y}_i)^2 \)).
-
Step 5: Summarise results
The
summarise()function computes the final values of SST, SSR, SSE, and \( R^2 \) by summing their respective components and performing the required calculations. -
Step 6: Print results
The
print()function displays the calculated values in the console.
Example Output
Key Takeaways
- The Tidyverse provides a pipeline-friendly approach, making the code cleaner and easier to follow.
- Intermediate calculations (e.g., SST, SSR, SSE components) are stored directly in the tibble, allowing for quick inspection or debugging.
- The relationship \( SST = SSR + SSE \) holds true, as verified by the results.
- Using Tidyverse functions like
mutate()andsummarise()simplifies complex workflows.
Implementation with stats Package
The stats package is a core part of R and includes functions for fitting linear models, performing statistical analyses, and calculating various components of regression analysis. In this section, we’ll compute SST, SSR, SSE, and \( R^2 \) using the stats package.
Step-by-Step Code
# Step 1: Create the dataset
hours <- c(2, 4, 6, 8, 10) # Independent variable
scores <- c(65, 75, 85, 90, 95) # Dependent variable
# Step 2: Fit the regression model
model_stats <- lm(scores ~ hours) # Linear regression model
# Step 3: Extract model summary
summary_stats <- summary(model_stats)
# Step 4: Use ANOVA to calculate SST, SSR, and SSE
anova_results <- anova(model_stats)
sst <- sum(anova_results["Sum Sq"]) # Total Sum of Squares
ssr <- anova_results["Sum Sq"][1, ] # Regression Sum of Squares
sse <- anova_results["Sum Sq"][2, ] # Error Sum of Squares
# Step 5: Extract R-squared from the model summary
r_squared <- summary_stats$r.squared
# Step 6: Print results
cat("SST:", sst, "\n")
cat("SSR:", ssr, "\n")
cat("SSE:", sse, "\n")
cat("R-squared:", r_squared, "\n")
Detailed Explanation
Here’s a breakdown of each step in the implementation:
-
Step 1: Create the dataset
The variables
hours(independent variable) andscores(dependent variable) represent the study hours and test scores, respectively. -
Step 2: Fit the regression model
The
lm()function from thestatspackage fits a linear regression model. Here,scoresis the dependent variable, andhoursis the independent variable. -
Step 3: Extract model summary
The
summary()function provides detailed information about the regression model, including \( R^2 \), coefficients, standard errors, t-values, and p-values. -
Step 4: Use ANOVA to calculate SST, SSR, and SSE
The
anova()function performs an analysis of variance on the fitted model and returns a table with the following key values:Sum Sq: The sum of squares for the regression and residual components.sst: The total sum of squares is the sum of allSum Sqvalues.ssr: The first value underSum Sq, representing the regression sum of squares.sse: The second value underSum Sq, representing the error sum of squares.
-
Step 5: Extract \( R^2 \) from the model summary
The coefficient of determination (\( R^2 \)) is directly available in the model summary under
r.squared. -
Step 6: Print results
The
cat()function displays the calculated values for SST, SSR, SSE, and \( R^2 \) in the console.
Example Output
Key Takeaways
- The
anova()function simplifies the computation of SST, SSR, and SSE by providing the necessary components directly. - The relationship \( SST = SSR + SSE \) is verified through the results.
- High \( R^2 \) values (close to 1) indicate that the model explains most of the variability in the data.
- The
statspackage is part of R’s base installation, making it a reliable and efficient option for regression analysis.
Visualization
To better understand the components of regression analysis, let's visualize the data points, regression line, and the components SST, SSR, and SSE. Below is an R script to plot the three subplots showing each component with the observed data, the fitted line, and the mean.
# If required, install the gridExtra package
if (!requireNamespace("gridExtra", quietly = TRUE)) {
install.packages("gridExtra")
}
# Load required libraries
library(ggplot2)
library(gridExtra)
# Step 1: Create dataset
hours <- c(2, 4, 6, 8, 10)
scores <- c(65, 75, 85, 90, 95)
model <- lm(scores ~ hours)
predicted <- predict(model)
mean_score <- mean(scores)
# Step 2: Prepare data for visualization
df <- data.frame(hours, scores, predicted)
# Step 3: Plot SSR
plot_ssr <- ggplot(df, aes(x = hours)) +
geom_point(aes(y = scores), color = "blue", size = 3, label = "Observed Data") +
geom_line(aes(y = predicted), color = "red", size = 1, label = "Regression Line") +
geom_hline(yintercept = mean_score, color = "#006400", linetype = "dashed", label = "Mean Line") +
geom_segment(aes(xend = hours, y = mean_score, yend = predicted),
color = "red", linetype = "dotdash", alpha = 0.7) +
ggtitle("Regression Sum of Squares (SSR)") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5)) + # Center the title
ylab("Test Scores")
# Step 4: Plot SSE
plot_sse <- ggplot(df, aes(x = hours)) +
geom_point(aes(y = scores), color = "blue", size = 3, label = "Observed Data") +
geom_line(aes(y = predicted), color = "red", size = 1, label = "Regression Line") +
geom_hline(yintercept = mean_score, color = "#006400", linetype = "dashed", label = "Mean Line") +
geom_segment(aes(xend = hours, y = predicted, yend = scores),
color = "blue", linetype = "solid", alpha = 0.7) +
ggtitle("Error Sum of Squares (SSE)") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5)) + # Center the title
ylab("Test Scores")
# Step 5: Plot SST
plot_sst <- ggplot(df, aes(x = hours)) +
geom_point(aes(y = scores), color = "blue", size = 3, label = "Observed Data") +
geom_hline(yintercept = mean_score, color = "#006400", linetype = "dashed", label = "Mean Line") +
geom_segment(aes(xend = hours, y = mean_score, yend = scores),
color = "#006400", linetype = "dotted", alpha = 0.7) +
ggtitle("Total Sum of Squares (SST)") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5)) + # Center the title
xlab("Study Hours") +
ylab("Test Scores")
# Step 6: Combine all plots
grid.arrange(plot_ssr, plot_sse, plot_sst, ncol = 1)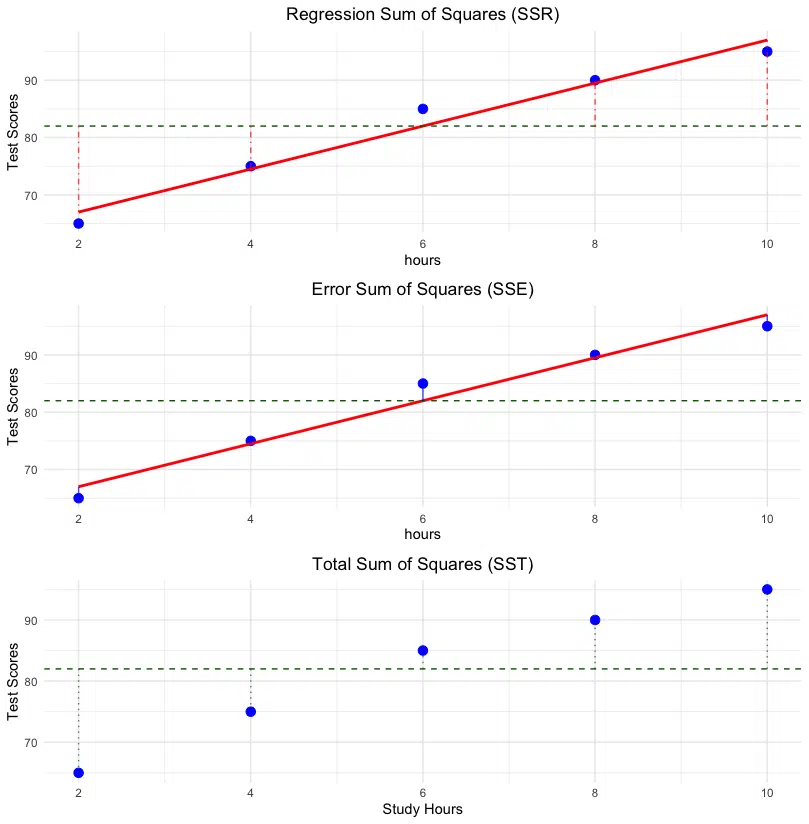
The figure consists of three subplots that highlight the relationships between SST, SSR, and SSE:
- Regression Sum of Squares (SSR): The first subplot shows how the regression line captures the explained variation in the data. Vertical lines represent the differences between the predicted values and the mean of the observed data.
- Error Sum of Squares (SSE): The second subplot visualizes the residuals or errors, which are the differences between the observed data and the predicted values. Vertical lines illustrate these discrepancies.
- Total Sum of Squares (SST): The final subplot demonstrates the total variability of the observed data around the mean. The regression line is included for context, and vertical lines represent the differences between the observed values and the mean.
Together, these plots emphasize the fundamental relationship:
This equation illustrates how the total variability (SST) is partitioned into the variability explained by the model (SSR) and the unexplained variability (SSE). Observing these components separately provides insight into the regression model's performance and fit quality.
Complete R Implementation
This section combines everything covered so far into a single, complete workflow. The script calculates SST, SSR, SSE, and \( R^2 \), visualizes the components, and outputs a clean summary of results. This implementation is modular, making it easy to adapt to other datasets.
# Step 1: Load required libraries
if (!requireNamespace("gridExtra", quietly = TRUE)) {
install.packages("gridExtra")
}
library(ggplot2)
library(gridExtra)
library(tidyverse)
# Step 2: Define a function for analysis
analyze_regression <- function(data, x_var, y_var) {
# Fit model
formula <- as.formula(paste(y_var, "~", x_var))
model <- lm(formula, data = data)
# Add predictions and calculations to the data
data <- data %>%
mutate(
predicted = predict(model),
mean_y = mean(!!sym(y_var)),
sst_comp = (!!sym(y_var) - mean_y)^2,
ssr_comp = (predicted - mean_y)^2,
sse_comp = (!!sym(y_var) - predicted)^2
)
# Summarize results
results <- data %>%
summarise(
sst = sum(sst_comp),
ssr = sum(ssr_comp),
sse = sum(sse_comp),
r_squared = ssr / sst
)
# Create visualization plots
plot_ssr <- ggplot(data, aes(x = !!sym(x_var))) +
geom_point(aes(y = !!sym(y_var)), color = "blue", size = 3) +
geom_line(aes(y = predicted), color = "red", size = 1) +
geom_hline(yintercept = mean(data[[y_var]]), color = "#006400", linetype = "dashed") +
geom_segment(aes(xend = !!sym(x_var), y = mean_y, yend = predicted),
color = "red", linetype = "dotdash", alpha = 0.7) +
ggtitle("Regression Sum of Squares (SSR)") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5)) +
ylab(y_var)
plot_sse <- ggplot(data, aes(x = !!sym(x_var))) +
geom_point(aes(y = !!sym(y_var)), color = "blue", size = 3) +
geom_line(aes(y = predicted), color = "red", size = 1) +
geom_hline(yintercept = mean(data[[y_var]]), color = "#006400", linetype = "dashed") +
geom_segment(aes(xend = !!sym(x_var), y = predicted, yend = !!sym(y_var)),
color = "blue", linetype = "solid", alpha = 0.7) +
ggtitle("Error Sum of Squares (SSE)") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5)) +
ylab(y_var)
plot_sst <- ggplot(data, aes(x = !!sym(x_var))) +
geom_point(aes(y = !!sym(y_var)), color = "blue", size = 3) +
geom_hline(yintercept = mean(data[[y_var]]), color = "#006400", linetype = "dashed") +
geom_segment(aes(xend = !!sym(x_var), y = mean_y, yend = !!sym(y_var)),
color = "#006400", linetype = "dotted", alpha = 0.7) +
ggtitle("Total Sum of Squares (SST)") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5)) +
xlab(x_var) +
ylab(y_var)
# Combine all plots
combined_plot <- grid.arrange(plot_ssr, plot_sse, plot_sst, ncol = 1)
# Return results
list(
model = model,
results = results,
plots = combined_plot,
data = data
)
}
# Step 3: Example usage
df <- tibble(
hours = c(2, 4, 6, 8, 10),
scores = c(65, 75, 85, 90, 95)
)
analysis <- analyze_regression(df, "hours", "scores")
print(analysis$results)
Detailed Explanation
The implementation includes three key components:
-
Data Preparation: The function uses
mutate()to calculate SST, SSR, and SSE components directly in the data. -
Visualization: Subplots for SST, SSR, and SSE are created using
ggplot2, with the regression line, mean line, and appropriate vertical lines to represent components. -
Results Summary: The
summarise()function calculates the total SST, SSR, SSE, and \( R^2 \), which are returned as a summary table.
Example Output
Key Takeaways
- This function encapsulates the entire workflow, making it reusable for any dataset.
- Visualizations are modular and highlight the relationships between SST, SSR, and SSE.
- The calculated results verify the relationship \( SST = SSR + SSE \) and provide a clear measure of \( R^2 \).
- The modular approach makes it easy to extend the function with additional analysis or visualizations.
Using car Package
The car (Companion to Applied Regression) package in R provides advanced tools for regression analysis, including ANOVA tables and diagnostic methods. This section demonstrates how to use the car package to compute SST, SSR, and SSE efficiently and generate ANOVA summaries.
Step-by-Step Code
# If required, install the car package
if (!requireNamespace("car", quietly = TRUE)) {
install.packages("car")
}
# Load the car package
library(car)
# Step 1: Create the dataset
hours <- c(2, 4, 6, 8, 10)
scores <- c(65, 75, 85, 90, 95)
# Step 2: Fit the regression model
model_car <- lm(scores ~ hours)
# Step 3: Compute ANOVA table
anova_table <- Anova(model_car, type = "II")
# Step 4: Extract SST, SSR, and SSE
sst <- sum(anova_table$`Sum Sq`) # Total Sum of Squares
ssr <- anova_table$`Sum Sq`[1] # Regression Sum of Squares
sse <- anova_table$`Sum Sq`[2] # Error Sum of Squares
# Step 5: Compute R-squared
r_squared <- summary(model_car)$r.squared
# Step 6: Print results
cat("SST:", sst, "\n")
cat("SSR:", ssr, "\n")
cat("SSE:", sse, "\n")
cat("R-squared:", r_squared, "\n")
# Step 7: Display the ANOVA table
print(anova_table)
Detailed Explanation
The `car` package simplifies the calculation of sum of squares and provides a more detailed ANOVA output. Here’s a breakdown of the workflow:
-
Step 1: Create the dataset
The variables
hoursandscoresrepresent the independent and dependent variables, respectively. -
Step 2: Fit the regression model
The
lm()function is used to fit a linear regression model. Here,scoresis modeled as a function ofhours. -
Step 3: Compute the ANOVA table
The
Anova()function generates an ANOVA table, which includes the sum of squares for each term in the model. -
Step 4: Extract SST, SSR, and SSE
The total sum of squares (
SST) is the sum of allSum Sqvalues in the ANOVA table. The regression sum of squares (SSR) corresponds to the first row of the table, while the error sum of squares (SSE) corresponds to the second row. -
Step 5: Compute \( R^2 \)
The coefficient of determination (\( R^2 \)) is calculated directly from the model summary using
summary(model_car)$r.squared. -
Step 6: Print results
The results for SST, SSR, SSE, and \( R^2 \) are displayed in the console using the
cat()function. -
Step 7: Display the ANOVA table
The
print()function outputs the detailed ANOVA table, which provides additional insights into the model terms and their contributions to the overall variability.
Example Output
Understanding the ANOVA Table
The ANOVA table generated by the car package provides a breakdown of the variability in the data. Here’s what each term represents:
-
Sum Sq:
The sum of squares for each term in the model. For example:
hours: Regression Sum of Squares (SSR), the variation explained by the predictor variable.Residuals: Error Sum of Squares (SSE), the variation unexplained by the model.
The total sum of squares (SST) is the sum of these values: \( SST = SSR + SSE \).
-
Df:
Degrees of freedom associated with each term. For example:
hours: 1 degree of freedom because there’s one predictor variable.Residuals: 3 degrees of freedom, calculated as \( n - k - 1 \), where \( n \) is the number of observations, and \( k \) is the number of predictors.
-
F value:
The F-statistic tests whether the predictor variable significantly contributes to explaining the variability in the response variable. A higher F-value indicates greater significance.
-
Pr(>F):
The p-value associated with the F-statistic. It indicates the probability of observing an F-value as extreme as the calculated value under the null hypothesis (i.e., the predictor variable has no effect). Small p-values (e.g., < 0.05) indicate statistical significance.
-
Significance Codes:
A shorthand interpretation of the p-value:
***: Highly significant (p < 0.001)**: Significant (p < 0.01)*: Moderate significance (p < 0.05).: Weak significance (p < 0.1)- Blank: Not significant (p ≥ 0.1)
Together, these components provide a detailed view of how the predictor variable contributes to the variability in the response variable and the overall model fit.
Key Takeaways
- The
carpackage simplifies regression analysis by providing detailed ANOVA tables. - The relationship \( SST = SSR + SSE \) is verified using the ANOVA table output.
- The \( R^2 \) value confirms the proportion of variability explained by the model.
- This method is particularly useful for models with multiple terms, as it partitions the sum of squares by term.
Using modelr Package
The modelr package is part of the Tidyverse ecosystem and provides utilities for working with models in a pipeline-friendly way. It allows you to easily add predictions, residuals, and other calculations to your dataset for further analysis and visualization. This section demonstrates how to calculate SST, SSR, and SSE using modelr.
Step-by-Step Code
# If required, install the modelr package
if (!requireNamespace("modelr", quietly = TRUE)) {
install.packages("modelr")
}
# Load required libraries
library(modelr)
library(tidyverse)
# Step 1: Create the dataset
df <- tibble(
hours = c(2, 4, 6, 8, 10),
scores = c(65, 75, 85, 90, 95)
)
# Step 2: Fit the regression model
model <- lm(scores ~ hours, data = df)
# Step 3: Add predictions and residuals to the dataset
df <- df %>%
add_predictions(model) %>% # Adds predicted values as a column
add_residuals(model) # Adds residuals (y - y_pred) as a column
# Step 4: Calculate SST, SSR, and SSE
sst <- df %>%
summarise(sst = sum((scores - mean(scores))^2)) %>%
pull(sst)
ssr <- df %>%
summarise(ssr = sum((pred - mean(scores))^2)) %>%
pull(ssr)
sse <- df %>%
summarise(sse = sum(resid^2)) %>%
pull(sse)
# Step 5: Compute R-squared
r_squared <- ssr / sst
# Step 6: Print results
cat("SST:", sst, "\n")
cat("SSR:", ssr, "\n")
cat("SSE:", sse, "\n")
cat("R-squared:", r_squared, "\n")
Detailed Explanation
Here’s a breakdown of each step in the workflow:
-
Step 1: Create the dataset
A
tibbleis created containing the independent variable (hours) and the dependent variable (scores). -
Step 2: Fit the regression model
The
lm()function fits a linear regression model, wherescoresis the response variable andhoursis the predictor. -
Step 3: Add predictions and residuals
The
add_predictions()function appends a column to the dataset containing the predicted values (\( \hat{y}_i \)) for each observation. Theadd_residuals()function appends another column with the residuals (\( y_i - \hat{y}_i \)), which represent the errors. -
Step 4: Calculate SST, SSR, and SSE
Using the updated dataset, the components are calculated as follows:
sst: Total sum of squares, calculated as the sum of squared differences between the observed values and their mean.ssr: Regression sum of squares, calculated as the sum of squared differences between the predicted values and the mean of the observed values.sse: Error sum of squares, calculated as the sum of squared residuals.
-
Step 5: Compute R-squared
The coefficient of determination (\( R^2 \)) is computed as the proportion of the total variability explained by the model: \( R^2 = \text{SSR} / \text{SST} \).
-
Step 6: Print results
The calculated values are displayed in the console using the
cat()function.
Example Output
Key Takeaways
-
The
modelrpackage integrates seamlessly with the Tidyverse, making it easy to add predictions and residuals to datasets. - The calculated components verify the relationship \( SST = SSR + SSE \), and the \( R^2 \) value confirms the proportion of variance explained by the model.
- The pipeline-friendly approach minimizes code duplication and enhances readability.
- This method can be easily extended to include more diagnostic calculations or visualizations.
Conclusion
R offers diverse and powerful methods to calculate and analyze the sum of squares components in regression analysis. From base R to Tidyverse and specialized packages like car and modelr, you can tailor your approach based on your workflow preferences and project requirements. These methods enable precise evaluation of model performance through SST, SSR, and SSE.
Key Takeaways:
- Base R: Offers direct, formula-based methods for calculating sum of squares components, ideal for understanding fundamental principles.
- Tidyverse: Provides a pipeline-friendly and readable approach, simplifying workflows for larger datasets.
- Specialized Packages: Tools like
carandmodelrextend functionality for in-depth analysis and modeling convenience. - Visualization: Plays a crucial role in understanding the relationships between SST, SSR, and SSE, improving model interpretability.
If you'd like to explore more about regression analysis or try out our interactive tools, visit the Further Reading section for additional resources and calculators.
Have fun and happy learning!
Further Reading
Expand your knowledge with these additional resources. Whether you're looking for interactive tools, package documentation, or in-depth guides, these links will help you dive deeper into the concepts covered in this guide.
-
Residual Sum of Squares (RSS) Calculator
Use this calculator to compute the Residual Sum of Squares, an essential measure for evaluating model accuracy.
-
Explained Sum of Squares (ESS) Calculator
Calculate the Explained Sum of Squares to understand how much variation is explained by your model.
-
Total Sum of Squares (TSS) Calculator
Determine the Total Sum of Squares, which measures the overall variability in the dataset.
-
Coefficient of Determination (R²) Calculator
Find the R² value to assess the proportion of variance explained by your regression model.
-
Understanding Sum of Squares: SST, SSR, and SSE
A comprehensive guide to understanding and calculating different types of sum of squares in regression analysis, featuring interactive examples and step-by-step calculations.
-
SST, SSR, and SSE Calculations in Python: A Comprehensive Guide
A comprehensive guide to calculating Sum of Squares components (SST, SSR, SSE) in Python, featuring interactive examples and step-by-step implementations.
-
ggplot2: Create Elegant Data Visualizations
Learn to create data visualizations in R using the powerful ggplot2 package.
-
dplyr: Data Manipulation in R
Master data manipulation and transformation tasks using dplyr, part of the Tidyverse.
-
tidyr: Data Cleaning and Reshaping
Reshape and clean your datasets efficiently using the tidyr package.
-
broom: Tidy Model Outputs
Tidy up your regression model outputs for better readability and analysis.
-
car: Companion to Applied Regression
Explore advanced regression analysis methods and diagnostics using the car package.
-
modelr: Modelling Functions for Tidy Data
Simplify your model-building workflow with modelr's tidyverse-compatible tools.
-
stats: R Core Statistics Functions
Utilize the built-in stats package for regression modeling and statistical tests.
Attribution and Citation
If you found this guide and tools helpful, feel free to link back to this page or cite it in your work!
