How to Calculate Implied Volatility in R

Implied volatility tells us the expected volatility of a stock over an option’s lifetime. Implied volatility is directly influenced by the supply and demand of the options and the market’s expectation of the direction of the price of the underlying security. As expectations rise or the demand for an option increases, implied volatility will increase. As implied volatility increases, the option price increases.

On the other hand, as the market’s expectations decrease or the demand for an option falls, implied volatility will also fall. As implied volatility decreases, the option price decreases.

This tutorial will go through an option’s implied volatility and how to calculate it with R. We will consider root-finding methods to calculate implied volatility: Newton-Raphson, Interval Bisection, and Brute Force.

---

What is Implied Volatility?

Before going through implied volatility, you should have gone through the Black-Scholes formula and the Options Greeks.

We can use the Black-Scholes Formula to price a European option. We need five variables: stock price, exercise price, time to expiration, risk-free interest rate, and standard deviation of log returns or volatility. Let’s look at a diagram describing a European call option.

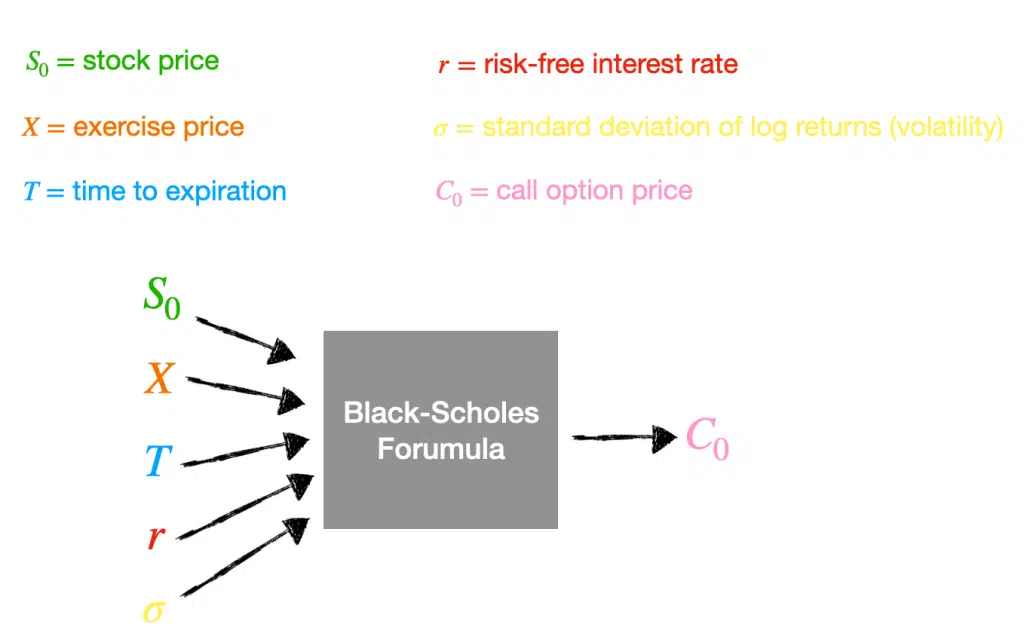
The first four variables are easy to find. We can easily find the stock price. The exercise price is part of the contract. We can approximate the risk-free interest rate by assuming it equals the interest rate on a three-month government Treasury bill. The time to expiration we can calculate using today’s date and when the contract will expire. However, volatility is tricky; it is not a constant value.

We can estimate the volatility of an option by looking at the history of the standard deviation of log returns.

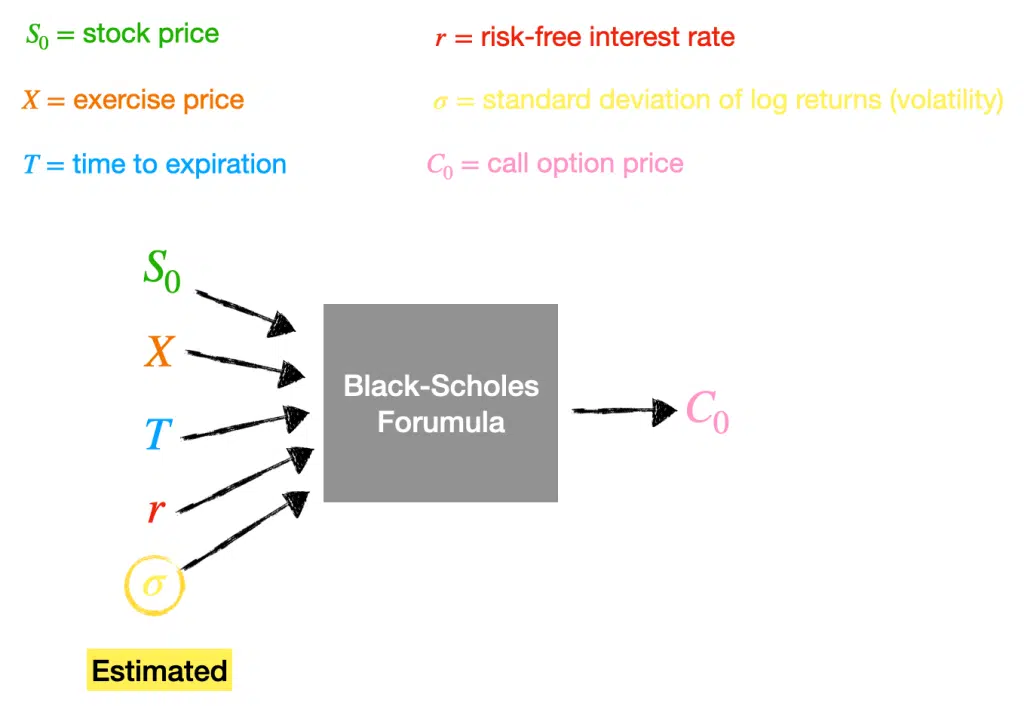
Any volatility value is an estimate, and there is an assumption that this variable will be constant over the option’s lifetime.

However, options are traded constantly, and we can look up the market price for a call option for a given stock price, exercise price, risk-free interest rate and time to expiration.

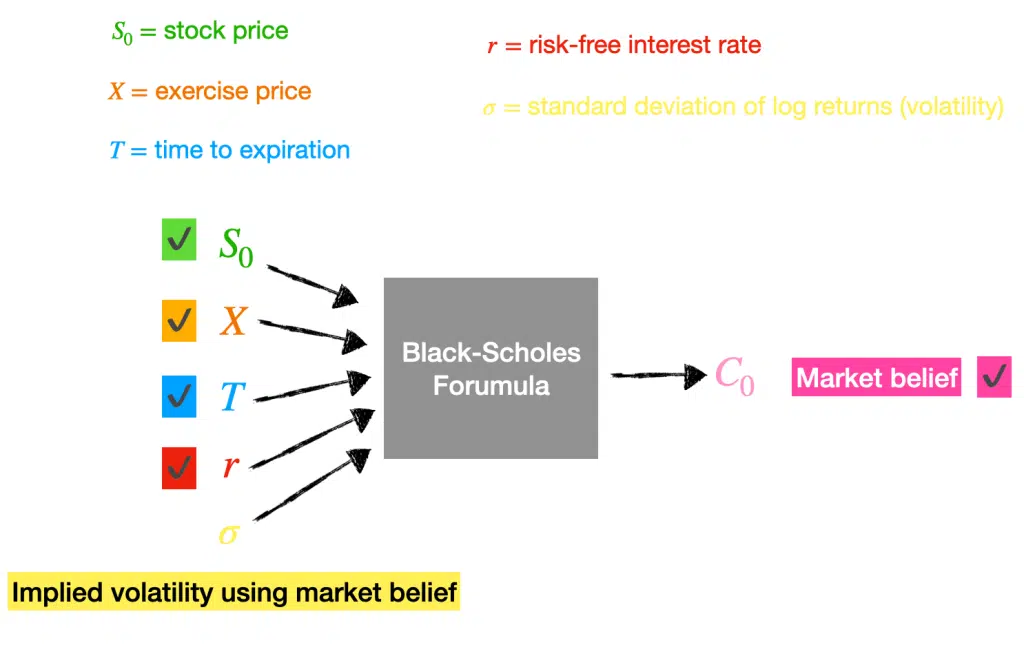
Suppose we know the market price or what the market believes the option price should be based on transactions and known variables. In that case, we can work backwards through Black-Scholes to determine the market estimate for the volatility or implied volatility.

If the market gets more unpredictable, the market will pay more for a given option, driving the implied volatility up. We can aggregate the implied volatility across multiple securities to find implied volatility for given markets at a time.

Remember, the implied volatility depends on an option’s market price, not the other way around.

Let’s look at the Black-Scholes formula for pricing a European call option:

$$C= S_{0}N(d_{1})~- Xe^{-r\tau}N(d_{2}) $$

where,

$$d_{1} = \frac{\text{ln}\frac{S_{0}}{X} + (r + \sigma^{2}/2)*\tau}{\sigma\sqrt{\tau}}, \qquad d_{2} = \frac{\text{ln}\frac{S_{0}}{X} + (r – \sigma^{2}/2)*\tau}{\sigma\sqrt{\tau}} = d_{1} – \sigma\sqrt{\tau}$$

• S: current underlying price
• K: strike price of option
• r: risk-free interest rate
• T: time until option expiration
• $\sigma: ~\text{annual volatility of underlying security’s returns}$
• N(x): cumulative distribution function for a standard normal distribution

Let’s say we want to find the implied volatility for an option with a current price for the underlying at \$100 for the right to buy the stock a year from the current date for \$125. The call option costs \$25, and the risk-free interest rate is 5%. If we put all of these values in the Black-Scholes formula, we will get the following:

$$25= 100 * N(\frac{\text{ln}\frac{100}{125} + (0.05 + \sigma^{2}/2)*1}{\sigma\sqrt{1}})~- 125e^{-0.05*1}N(\frac{\text{ln}\frac{100}{125} + (0.05 – \sigma^{2}/2)*1}{\sigma\sqrt{1}} $$

The unknown value in this equation is the volatility. We need to solve for volatility in the equation to return a call price of $18. We can solve this equation using iterative methods.

Now let’s look at the iterative methods to find the implied volatility in R.

---

Implied volatility using Newton Raphson Method

The first method we will look at is the Newton-Raphson method. The Newton-Raphson method is a way to quickly find an approximation for the root of a real-valued function. The method considers that a straight-line tangent can approximate a continuous and differentiable function.

Newton Raphson Algorithm

1. $\text{Define a continuous, differentiable function}~ f(x)$
2. $\text{Take an initial guess for the root}~ x = x_{0},~\text{approximate the root guess with}~ x_{1} = \frac{f(x_{0})}{f'(x_{0})}.$
3. $\text{Iterate as follows:}~ x_{n+1} = x_{n} – \frac{f(x_{n})}{f'(x_{n})}$
4. $\text{Break if}~ |f(x_{n})| < \epsilon.~ \text{Where}~ \epsilon ~\text{is the tolerance for error}.$

When we apply the Newton-Raphson Algorithm to solve for implied volatility, we get the following:

1. $\text{Our continuous, differentiable function is: }~f(\sigma) = V_{BS_{\sigma}} – V_{market}$
2. $\text{Our initial guess is}~\sigma_{0} = 0.30$
3. $\text{Iterate as follows:}~ \sigma_{n+1} = \sigma_{n} – \frac{V_{BS_{\sigma}} – V_{market}}{\frac{\partial V_{BS_{\sigma}}}{\partial \sigma}}$
4. $\text{Break if}~ |V_{BS_{\sigma}} – V_{market}| < \epsilon,~ \text{return}~ \sigma_{n}.$

R Code for Newton-Raphson

First, we will define the Black-Scholes function:

bsm_func <- function(S, K, r, T, sig, option_type){
    
    if (option_type=="C") {
        d1 <- (log(S/K) + (r + sig^2/2)*T) / (sig*sqrt(T))
        d2 <- (log(S/K) + (r - sig^2/2)*T) / (sig*sqrt(T))
        val <- S*pnorm(d1) - K*exp(-r*T)*pnorm(d2)
        print(val)
        return (val)
    }
  if (option_type=="P") {
        d1 <- (log(S/K) + (r + sig^2/2)*T) / (sig*sqrt(T))
        d2 <- (log(S/K) + (r - sig^2/2)*T) / (sig*sqrt(T))
        val <-  K*exp(-r*T)*pnorm(-d2) - S*pnorm(-d1)
        print(val)
        return (val)
    }
}

Next, we will define the function for calculating the vega of an option:

vega <- function(S, K, r, T, sigma){
d1 <- (log(S/K) + (r + sigma^2/2)*T) / (sigma*sqrt(T))
vega = S * sqrt(T) * dnorm(d1)
return (vega)
}

Now we can put it all together and find the implied volatility using the Newton-Raphson algorithm:

implied_volatility_nr <- function(C, S, K, r, T, cp, tol=0.0001, max_iterations=100) {
    sigma = 0.3
    print(cp)
    print(C)
    for(i in 1:100){
        print(i)
        print('before market price')
        market_price = bsm_func(S, K, r, T, sigma, cp)
        print(market_price)
        print('before diff')

        diff = market_price - C
        print(diff)
        print('before diff < tol')

        if (abs(diff) < tol)
            break
        print('before sigma change')

        sigma = sigma - diff / vega(S,K,r,T,sigma)
    }
    return (sigma * 100)
}

Let’s test the code for a call option

library(glue)
s=100
K=125
r=0.05
T=1
obs_price = 25
imp_vol = implied_volatility_nr(obs_price, S, K, r, T, "C")
glue('Implied Volatility using Newton Raphson is {format(round(imp_vol,2), nsmall=2)}%')

Implied Volatility using Newton Raphson is 79.18%

We found the implied volatility for the call option to be 79.18%.

If we plug the implied volatility value into the Black-Scholes formula, we will get the market price for the call option.

imp_vol = implied_volatility_nr(obs_price, S, K, r, T, "C")
price = bsm_func(S, K, r, T, imp_vol/100, "C")
glue('Option price using implied volatility from Newton-Raphson method is: ${format(round(price,2), nsmall=2)}')

Option price using implied volatility from Newton-Raphson method is: $25.00

Let’s test the code for the put option.

library(glue)
imp_vol = implied_volatility_nr(obs_price, S, K, r, T, "P")
glue('Implied Volatility using Newton Raphson is {format(round(imp_vol,2), nsmall=2)}%')

Implied Volatility using Newton Raphson is 31.11%

We found the implied volatility for the put option to be 31.11%

If we plug the implied volatility value into the Black-Scholes formula, we will get the market price for the put option.

imp_vol = implied_volatility_nr(obs_price, S, K, r, T, "P")
price = bsm_func(S, K, r, T, imp_vol/100, "P")
glue('Put Option price using implied volatility from Newton-Raphson method is: ${format(round(price,2), nsmall=2)}')

Put Option price using implied volatility from Newton-Raphson method is: $25.00

Implied Volatility Using Interval Bisection Method

The second method we will look at is the Interval Bisection method. The interval bisection method does not require numerical derivatives to calculate the implied volatility.

Interval Bisection Algorithm

1. $\text{Choose} ~\sigma_{a} ~\text{and} ~\sigma_{b} \text{with} ~\sigma_{a} < \sigma_{b} ~\text{and} ~\sigma_{b} – \sigma_{a} > \epsilon$
2. $\text{Set}~ \sigma_{mid} := \frac{(\sigma_{a} + \sigma_{b})}{2}~ \text{and evaluate}~ BS_{\sigma_{mid}}$
3. $\text{If}~ (BS_{\sigma_{mid}} – BS_{market}) > 0 ~\text{then}~ \sigma_{b} = \sigma_{mid}. ~\text{Otherwise reset}~ \sigma_{a} = \sigma_{mid}$
4. $\text{If}~ \sigma_{b} – \sigma_{a} < \epsilon~ \text{then stop. Use}~ \frac{(\sigma_{a} + \sigma_{b})}{2} ~\text{as the approximation to the root of function. Otherwise return to Step 2.}$

R code for Interval Bisection

Let’s look at the function to implement the interval bisection method:

implied_volatility_ib <- function(C, a, b, epsilon, S, K, r, T, cp) {
     x = (a + b) * 0.5
     
    while( b - a > epsilon){
        x = (a+b)*0.5
        price = bsm_func(S, K, r, T, x, cp)
        if (price - C > 0){
            b = (a + b) / 2
        }
        else{
            a = (a + b) / 2
        }
    }
    return (x * 100)
}

Let’s apply the interval bisection root-finding method to find the implied volatility of a call option.

obs_price = 25
S= 100
K=125
T=1
r=0.05
a = 0.005
b = 1.15
epsilon = 0.0001

imp_vol = implied_volatility_ib(obs_price, a, b, epsilon, S, K, r, T, "C")
glue('Implied Volatility using Interval Bisection is {format(round(imp_vol,2), nsmall=2)}%')

Implied Volatility using Interval Bisection is 79.18%

The implied volatility is 79.18%, the same value found using the Newton-Raphson method.

If we plug the implied volatility value into the Black-Scholes formula, we will get the market price for the call option:

imp_vol = implied_volatility_ib(obs_price, a, b, epsilon, S, K, r, T, "C")
price = bsm_func(S, K, r, T, imp_vol/100, "C")
glue('Option price using implied volatility from Interval Bisection method is: ${format(round(price,2), nsmall=2)}')

Option price using implied volatility from Interval Bisection method is: $25.00

Let’s apply the interval bisection method for a put option.

obs_price = 25
S= 100
K=125
T=1
r=0.05
a = 0.005
b = 1.15
epsilon = 0.0001

imp_vol = implied_volatility_ib(obs_price, a, b, epsilon, S, K, r, T, "P")
glue('Implied Volatility using Interval Bisection is {format(round(imp_vol,2), nsmall=2)}%')

Implied Volatility using Interval Bisection is 31.10%

We can see that the implied volatility is 31.10%, the same value found using the Newton-Raphson method to one decimal place.

If we plug the implied volatility value into the Black-Scholes formula, we will get the market price for the put option:

imp_vol = implied_volatility_ib(obs_price, a, b, epsilon, S, K, r, T, "P")
price = bsm_func(S, K, r, T, imp_vol/100, "P")
glue('Put Option price using implied volatility from Interval Bisection method is: ${format(round(price,2), nsmall=2)}')

Put Option price using implied volatility from Interval Bisection method is: $25.00

Implied Volatility Using Brute Force Method

The brute force method iterates through possible volatility candidates and finds the value that minimizes the absolute difference between the market price and the calculated Black-Scholes price or the root of the function.

Brute Force Algorithm

1. $\text{Define threshold}~\epsilon~\text{for when to accept the solution, e.g. when calculated price and actual market price within 1 cent}$
2. $\text{Define step variable to adjust the}~ \sigma ~\text{value}$
3. $\text{Take an initial guess for}~ \sigma$
4. $\text{If} ~BS_{market} – BS_{\sigma} > \epsilon~\text{ then}~ \sigma = \sigma + \text{step}.$
5. $\text{Else if} ~BS_{market} – BS_{\sigma} < 0 ~\text{and}~ | BS_{market} – BS_{\sigma}| > \epsilon~\text{, then}~ \sigma = \sigma – \text{step}.$
6. $\text{Else if} ~|BS_{market} – BS_{\sigma}| < \epsilon\text{, then}~ \text{choose} ~\sigma~ \text{as root of function}.$

R Code for Brute Force

Let’s look at the code for the brute force method:

implied_volatility_bf <- function(C, S, K, r, T, cp) {
    sigma = 0.5
    tol = 0.0001
    step = 0.0001     
    for (i in 1:10000){
        price = bsm_func(S, K, r, T, sigma, cp)
        diff = C - price
        if (diff > tol) {
            sigma = sigma + step
        }
         else if (diff < 0 && abs(diff) > tol){
            sigma = sigma - step
        } 
         else if (abs(diff) < tol) { 
            return (sigma * 100)
        }
    }
    return (sigma * 100)
}

Let’s apply the brute force method to the call option:

obs_price = 25
S= 100
K=125
T=1
r=0.05

imp_vol = implied_volatility_bf(obs_price, S, K, r, T, "C")
glue('Implied Volatility using Brute Force is {format(round(imp_vol,2), nsmall=2)}%')

Implied Volatility using Brute Force is 79.18%

The implied volatility is 79.18%, the same as the values found by the Newton-Raphson and Interval Bisection methods.

If we plug the implied volatility value back into the Black-Scholes formula, we will get the market price for the call option:

imp_vol = implied_volatility_bf(obs_price, S, K, r, T, "C")
price = bsm_func(S, K, r, T, imp_vol/100, "C")
glue('Call option price using implied volatility from Brute Force method is: ${format(round(price,2), nsmall=2)}')

Call option price using implied volatility from Brute Force method is: $25.00

Let’s apply the brute force method to the put option:

obs_price = 25
S= 100
K=125
T=1
r=0.05

imp_vol = implied_volatility_bf(obs_price, S, K, r, T, "P")
glue('Implied Volatility using Brute Force is {format(round(imp_vol,2), nsmall=2)}%')

Implied Volatility using Brute Force is 31.10%

The implied volatility is 31.10%, the same as the values found by the Newton-Raphson and Interval Bisection methods to one decimal place.

If we plug the implied volatility value into the Black-Scholes formula, we will get the market price for the put option:

imp_vol = implied_volatility_bf(obs_price, S, K, r, T, "P")
price = bsm_func(S, K, r, T, imp_vol/100, "P")
glue('Put option price using implied volatility from Brute Force method is: ${format(round(price,2), nsmall=2)}')

Put option price using implied volatility from Brute Force method is: $25.00

The brute force method is the slowest method out of the three.

If you want to learn how to calculate implied volatility in Python and C++, go to the articles:

• How to Calculate Implied Volatility in Python
• How to Calculate Implied Volatility in C++

Summary

Congratulations on reading to the end of this tutorial!

Go to the online courses page on R to learn more about coding in R for data science and machine learning.

For further reading on the Options Greeks, go to the article:

• How to Derive Options Greeks from the Black-Scholes Formula

You can use our free Black-Scholes option pricing calculator to estimate the fair value of a European call or put option.

You can use our free Implied Volatility calculator to estimate the Implied Volatility of a priced option.

Have fun, and happy researching!